
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теперь найдём собственные векторы
|
|
В данном примере получены различные собственные числа и каждому из них соответствует свой собственный вектор.
1) Рассмотрим собственное число 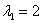 и подставим значение
и подставим значение 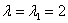 в однородную систему уравнений
в однородную систему уравнений 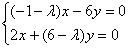 :
:
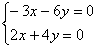
Для записи системы целесообразно запомнить формальный приём: мысленно либо на черновике подставляем 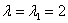 в определитель
в определитель 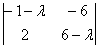 :
:
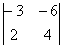 – это и есть коэффициенты системы.
– это и есть коэффициенты системы.
Из обоих уравнений следует:

Если в ходе решения выяснилось, что линейной зависимости нет (т.е. получается только тривиальное решение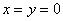 ) – ищите ошибку! Этот признак касается всех задач рассматриваемого типа.
) – ищите ошибку! Этот признак касается всех задач рассматриваемого типа.
Итак, в нашем распоряжении есть выражение 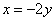 , и координаты собственного вектора
, и координаты собственного вектора 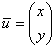 определены не однозначно. Стараемся подобрать значение «игрек» так, чтобы первая («иксовая») координата собственного вектора была целой, положительной и минимальной.
определены не однозначно. Стараемся подобрать значение «игрек» так, чтобы первая («иксовая») координата собственного вектора была целой, положительной и минимальной.
Пусть 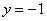 , тогда:
, тогда: 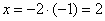
Обязательно проверяем, что частное решение 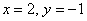 удовлетворяет каждому уравнению системы:
удовлетворяет каждому уравнению системы:
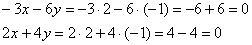
Таким образом: 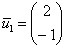
2) Найдём второй собственный вектор. Для этого мысленно либо на черновике подставим 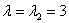 в определитель
в определитель 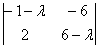 и запишем вторую однородную систему:
и запишем вторую однородную систему:
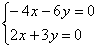
Из обоих уравнений следует, что 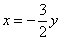 .
.
Положим 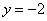 , тогда:
, тогда: 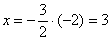
В результате, собственный вектор:  .
.
Повторим важные моменты решения:
– полученная система 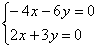 непременно имеет общее решение (уравнения линейно зависимы);
непременно имеет общее решение (уравнения линейно зависимы);
– «игрек» подбираем таким образом, чтобы первая «иксовая» координата была целой, положительной и как можно меньше.
– проверяем, что частное решение 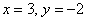 удовлетворяет каждому уравнению системы.
удовлетворяет каждому уравнению системы.
Ответ: собственные числа: 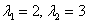 , собственные векторы:
, собственные векторы: 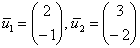 .
.
Промежуточных «контрольных точек» было вполне достаточно, поэтому проверка равенств 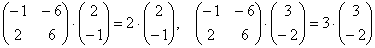 , в принципе, дело излишнее.
, в принципе, дело излишнее.
В различных источниках информации довольно часто собственные векторы записывают не в столбцы, а в строки, например: 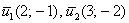 (и, если честно, я сам привык записывать их строками). Такой вариант вполне приемлем, но всё-таки «идеологически правильнее» использовать векторы-столбцы.
(и, если честно, я сам привык записывать их строками). Такой вариант вполне приемлем, но всё-таки «идеологически правильнее» использовать векторы-столбцы.
Возможно, решение показалась вам очень большим по объёму, но это только потому, что я очень подробно прокомментировал первый пример. На самом деле случай «два на два» – одно из самых простых и коротких заданий, которое только может встретиться в контрольной работе.
Пример 2
Найти собственные числа и собственные векторы матрицы
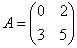
Примерный образец чистового оформления в конце урока.
Иногда требуется выполнить дополнительное задание, а именно:
Date: 2015-07-23; view: 946; Нарушение авторских прав