Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Взаимосвязь решений неоднородной и соответствующей однородной системы уравнений
|
|
Представьте двух близких родственниц: неоднородную систему (у которой хотя бы одно число правой части отлично от нуля) и такую же систему– только справа одни нули (то бишь, однородную систему). Нетрудно предположить, что если системы отличаются лишь столбцом свободных членов, то между их решениями должна существовать тесная связь. И это действительно так! Материал целесообразнее рассмотреть на конкретной задаче, которая, как и все другие, взята из реальной контрольной работы:
Пример 5
Дана система линейных алгебраических уравнений
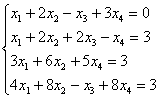
Требуется:
1) найти общее решение;
2) используя результат предыдущего пункта, найти общее решение соответствующей однородной системы и записать его в векторной форме.
Решение: по условию дана обычная неоднородная система уравнений, и первая часть не отличается новизной:
1) Запишем расширенную матрицу системы (не зеваем нолик в третьей строке) и с помощью элементарных преобразований приведём её к ступенчатому виду:
(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на –3. К четвёртой строке прибавили первую строку, умноженную на –4.
(2) Последние три строки одинаковы, две из них удалили.
Обратным ходом метода Гаусса получим общее решение:
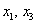– базисные переменные;
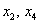– свободные переменные.
Выразим базисные переменные через свободные переменные. Из 2-го уравнения:
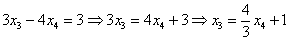– подставим в 1-ое уравнение:
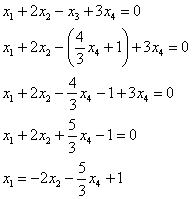
Общее решение неоднородной системы обозначим через 
(«Общее Неоднородной»).
Ответ: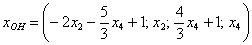 
2) Во второй части задания требуется найти общее решение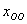 
такой же, только однородной системы 
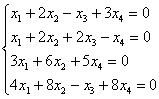, причём по условию необходимо использовать ответ предыдущего пункта.
Выполнять элементарные преобразования заново, разумеется, не нужно.
Правило: общее решение неоднородной системы равно сумме общего решения соответствующей однородной системы 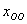и какого-либо частного решения неоднородной системы 
:
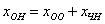
Откуда легко выражается общее решение нашей однородной системы:
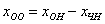
Найдём какое-нибудь частное решение неоднородной системы. Проще всего взять нулевые значения свободных переменных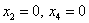 
:
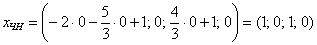
Таким образом, общее решение соответствующей однородной системы:
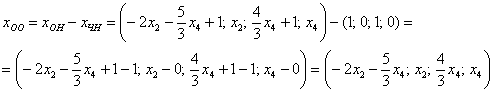
Представим 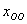в векторной форме. Поскольку у нас две свободные переменные, то фундаментальная система решений будет состоять из двух векторов.
Пойдём классическим путём:
Рассмотрим пару значений свободных переменных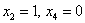 
и получим первый вектор:
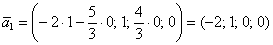– координаты данного вектора удовлетворяют каждому уравнению однородной системы (всегда желательна проверка!).
Теперь рассматриваем пару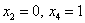 
и получаем второй вектор:
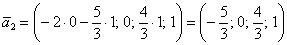– координаты данного вектора также удовлетворяют каждому уравнению однородной системы (тоже проверяем!).
И вообще – любая линейная комбинация векторов фундаментальной системы 
, где 
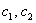– произвольные действительные числа, является решением данной системы:
Ответ: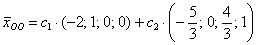 
, где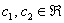 
Иными словами, если взять два любых вещественных числа, например,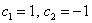 
, то получится вектор частного решения однородной системы:
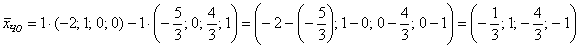, то есть набор 
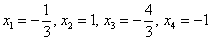удовлетворяет каждому уравнению однородной системы.
Если хотите избежать дробей, то при нахождении вектора 
следует выбрать значения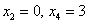 
и получить второй вектор в виде:
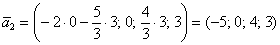
В этом случае ответ запишется в эквивалентной форме:
, где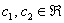
Порядком многих я, наверное, подзапутал, но коль скоро задание не придумано, то его нельзя было обойти стороной.
Более распространённая тема для самостоятельного решения:
Пример 6
Дана однородная система
Найти общее решение и записать ответ с помощью векторов фундаментальной системы. В образце решения завершающим элементарным преобразованием я уже потихоньку начинаю приобщать вас к методу Жордано-Гаусса.
Чтобы окончательно закрепить алгоритм, разберём финальное задание:
Пример 7
Решить однородную систему, ответ записать в векторной форме.
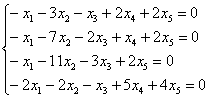
Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
(1) У первой строки сменили знак. Ещё раз заостряю внимание на неоднократно встречавшемся приёме, который позволяет существенно упростить следующее действие.
(1) Ко 2-ой и 3-ей строкам прибавили первую строку. К 4-ой строке прибавили первую строку, умноженную на 2.
(3) Последние три строки пропорциональны, две из них удалили.
В результате получена стандартная ступенчатая матрица, и решение продолжается по накатанной колее:
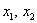– базисные переменные;
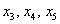– свободные переменные.
Выразим базисные переменные через свободные переменные. Из 2-го уравнения:
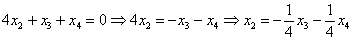– подставим в 1-ое уравнение:
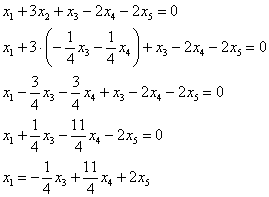
Таким образом, общее решение:
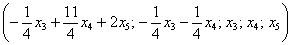
Поскольку в рассматриваемом примере три свободные переменные, то фундаментальная система содержит три вектора.
Подставим тройку значений 
в общее решение и получим вектор 
, координаты которого удовлетворяют каждому уравнению однородной системы. И снова повторюсь, что крайне желательно проверять каждый полученный вектор – времени займет не так много, а от ошибок убережёт стопроцентно.
Для тройки значений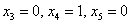 
находим вектор
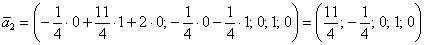
И, наконец, для тройки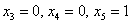 
получаем третий вектор:
Ответ: 
, где 
Желающие избежать дробных значений могут рассмотреть тройки 
и получить ответ в эквивалентном виде:
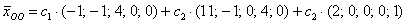
К слову о дробях. Посмотрим на полученную в задаче матрицу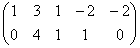 
и зададимся вопросом – нельзя ли упростить дальнейшее решение? Ведь здесь мы сначала выразили через дроби базисную переменную 
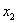, потом через дроби базисную переменную 
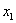, и, надо сказать, процесс это был не самый простой и не самый приятный.
Второй вариант решения:
Идея состоит в том, чтобы попытаться выбрать другие базисные переменные. Посмотрим на матрицу и заметим две единицы в третьем столбце. Так почему бы не получить ноль вверху? Проведём ещё одно элементарное преобразование:
(4) К первой строке прибавили вторую строку, умноженную на –1.
Здесь базисные переменные 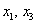легко и практически мгновенно выражаются через свободные переменные 
:
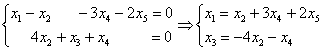
По существу, мы применили метод Жордано-Гаусса, который как раз и направлен на скорейшее получение базисного решения посредством дополнительных элементарных преобразований.
В результате общее решение: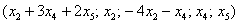 
Последовательно выбираем в качестве значений свободных неизвестных тройки
и подстановкой их в 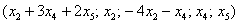получаем соответствующие векторы фундаментальной системы:
Не забываем проверить координаты каждого вектора!
Ответ: общее решение:
, где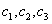 
– действительные числа.
Как видите, второй способ гораздо проще и рациональнее, но для подобных изысков, конечно, необходимо обладать некоторым опытом.
Надеюсь, данная статья окончательно развеяла все страхи перед векторами, и теперь вы с огромным удовольствием откроете учебник по линейной алгебре, чтобы изучить теорию векторных пространств, линейных преобразований и другие не менее интересные вещи.
Желаю успехов!
Решения и ответы:
Пример 2: Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
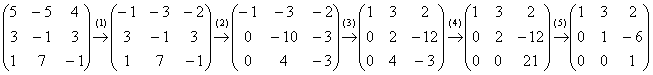(1) К первой строке прибавили вторую строку, умноженную на –2.
(2) Ко второй строке прибавили первую строку, умноженную на 3. К третьей строке прибавили первую строку.
(3) У первой строки сменили знак. Ко второй строке прибавили третью строку, умноженную на 3.
(4) К третьей строке прибавили вторую строку, умноженную на –2.
(5) Вторую строку разделили на 2, третью строку разделили на 21.
Ранг матрицы системы равен количеству переменных, значит, система имеет только тривиальное решение.
Ответ: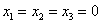 
Пример 4: Решение: запишем матрицу системы и с помощью элементарных преобразований приведем её ступенчатому виду:
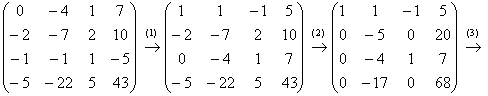
(1) У третьей строки сменили знак и переместили её на 1-ое место.
(2) Ко 2-ой и 4-ой строкам прибавили первую строку, умноженную на 2 и 5 соответственно.
(3) Вторую строку разделили на –5, 4-ую строку разделили на –17.
(4) Вторая и 4-ая строки одинаковы, последнюю строку удалили. К третьей строке прибавили вторую строку, умноженную на 4.
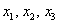– базисные переменные;
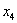– свободная переменная.
Выразим базисные переменные через свободную переменную.
Из последних двух уравнений:
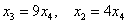– подставим в первое уравнение:
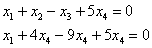
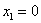
Таким образом, общее решение: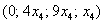 
Найдем вектор фундаментальной системы решений. Для этого выберем в качестве значения свободной неизвестной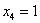 
:
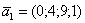
Ответ: общее решение однородной системы уравнений:
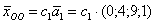, где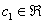 
(любое действительное число).
Пример 6: Решение: Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
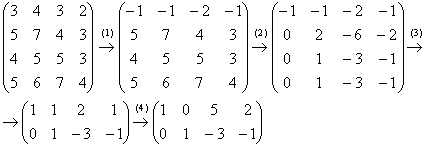
(1) К первой строке прибавили третью строку, умноженную на –1.
(2) Ко второй, третьей и четвертой строкам прибавили первую строку, умноженную на 5, 4 и 5 соответственно.
(3) Последние три строки пропорциональны, достаточно оставить только одну из них. У первой строки сменили знак.
(4) К первой строке прибавили вторую строку, умноженную на –1.
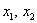– базисные переменные;
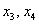– свободные переменные.
Выразим базисные переменные через свободные переменные:
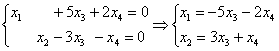
Таким образом, общее решение: 
.
Найдем векторы фундаментальной системы решений. Для этого последовательно выбираем в качестве значений свободных неизвестных следующие пары: 
и 
:
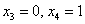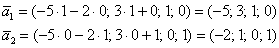
Ответ: общее решение: 
, где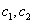 
– произвольные действительные числа.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Метод Жордано-Гаусса. Как найти обратную матрицу
с помощью элементарных преобразований?
Однажды некто Жордано (не путать с Джордано Бруно) сел решать очередную систему уравнений. Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе. Предположим, дана система с тремя уравнениями, тремя неизвестными и записана её расширенная матрица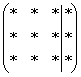 
. В наиболее распространенном случае получаются стандартные ступеньки 
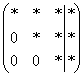, и так каждый день…. Одно и то же – как беспросветный ноябрьский дождь.
На некоторое время развевает тоску другой способ приведения матрицы к ступенчатому виду: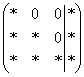 
, причём он совершенно равноценен и может быть не удобен только по причине субъективного восприятия. Но всё рано или поздно приедается…. И подумал тогда математик – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ 
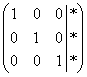с помощью дополнительных элементарных преобразований?
Для освоения данного урока «чайникам» придётся пойти путём Жордано и прокачать элементарные преобразования хотя бы среднего уровня, прорешав, минимум, 15-20 соответствующих заданий. Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:
Метод Гаусса для чайников;
Несовместные системы и системы с общим решением;
Ранг матрицы;
Однородные системы.
Ну, и совсем замечательно, если отработаны элементарные преобразования определителя.
Как все поняли, метод Жордано-Гаусса представляет собой модификацию метода Гаусса и с реализацией основной, уже озвученной выше идеи, мы встретимся на ближайших экранах. Кроме того, в число немногочисленных примеров данной статьи вошло важнейшее приложение – нахождение обратной матрицы с помощью элементарных преобразований.
Не мудрствуя лукаво:
Пример 1
Решить систему методом Жордано-Гаусса
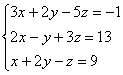
Решение: это первое задание урока Метод Гаусса для чайников, где мы 5 раз трансформировали расширенную матрицу системы и привели её к ступенчатому виду:
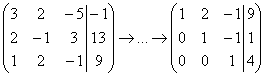
Теперь вместо обратного хода в игру вступают дополнительные элементарные преобразования. Сначала нам необходимо получить нули на этих местах: 
,
а потом ещё один ноль здесь: 
.
Идеальный с точки зрения простоты случай:
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.
(7) К первой строке прибавили вторую строку, умноженную на –2.
Не могу удержаться от иллюстрации итоговой системы:
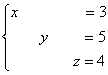
Ответ: 
Предостерегаю читателей от шапкозакидательского настроения – это был простейший демонстрационный пример. Для метода Жордано-Гаусса характерны свои специфические приёмы и не самые удобные вычисления, поэтому, пожалуйста, настройтесь на серьёзную работу:
Пример 2
Решить систему линейных уравнений методом Жордано-Гаусса.
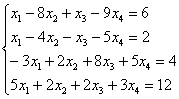
Решение: первая часть задания хорошо знакома:
(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на 3. К четвертой строке прибавили первую строку, умноженную на –5.
(2) Вторую строку разделили на 2, третью строку разделили на 11, четвёртую строку разделили на 3.
(3) Вторая и третья строки пропорциональны, 3-ю строку удалили. К четвёртой строке прибавили вторую строку, умноженную на –7
(4) Третью строку разделили на 2.
Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду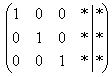 
.
Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, переставлять-то их можно, но в этом нет смысла. И далее целесообразно придерживаться следующего шаблона:
Находим наименьшее общее кратное чисел третьего столбца (1, –1 и 3), т.е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковыепо модулючисла, и этими соображениями обусловлено 5-ое преобразование матрицы:
(5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это было бы менее удобно для следующего действия. К хорошему привыкаешь быстро:
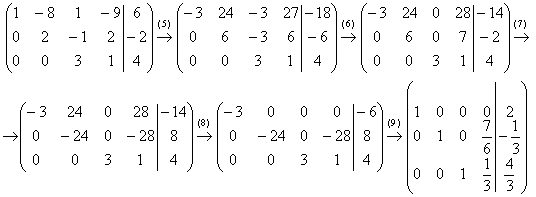
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.
(7) Во втором столбце два ненулевых значения (24 и 6) и нам снова нужно получить одинаковые по модулю числа. В данном случае всё сложилось довольно удачно – наименьшее кратное 24, и эффективнее всего умножить вторую строку на –4.
(8) К первой строке прибавили вторую.
(9) Заключительный штрих: первую строку разделили на –3, вторую строку разделили на –24 и третью строку разделили на 3. Это действие выполняется В ПОСЛЕДНЮЮ ОЧЕРЕДЬ! Никаких преждевременных дробей!
В результате элементарных преобразований получена эквивалентная исходной система:
Элементарно выражаем базисные переменные через свободную:
и записываем:
Ответ: общее решение: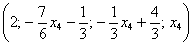 
В подобных примерах применение рассмотренного алгоритма чаще всего оправдано, поскольку обратный ход метода Гаусса обычно требует трудоёмких и неприятных вычислений с дробями.
И, разумеется, крайне желательна проверка, которая выполняется по обычной схеме, рассмотренной на уроке Несовместные системы и системы с общим решением.
Для самостоятельного решения:
Пример 3
Найти базисное решение с помощью элементарных преобразований
Такая формулировка задачи предполагает использование метода Жордано-Гаусса, и в образце решения матрица приводится к стандартному виду 
с базисными переменными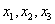 
. Однако всегда держите на заметке, что в качестве базисных можно выбрать и другие переменные. Так, например, если в первом столбце громоздкие числа, то вполне допустимо привести матрицу к виду 
(базисные переменные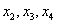 
), или к виду 
(базисные переменные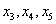 
), или даже к виду 
с базисными переменными 
. Существуют и другие варианты.
Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических жордановсих результатов вроде 
. Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-ом столбце есть два готовых нуля.
Примечание: термин «базис» имеет алгебраический смысл и понятие геометрического базиса здесь не при чём!
Если в расширенной матрице данных размеров вдруг обнаруживается пара линейно зависимых строк, то её следует попытаться привести к привычному виду 
с базисными переменными 
. Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений, причём там выбран другой базис.
Продолжаем совершенствовать свои навыки на следующей прикладной задаче:
Date: 2015-07-23; view: 1266; Нарушение авторских прав