
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Сколько у матрицы собственных чисел и собственных векторов?
|
|
У квадратной матрицы размером 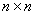 существует ровно
существует ровно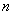 собственных значений, причём некоторые из них (или даже все) могут быть кратными (совпавшими).
собственных значений, причём некоторые из них (или даже все) могут быть кратными (совпавшими).
Так, у демонстрационной квадратной матрицы 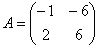 ровно два собственных значения, причём одно из них нам уже известно:
ровно два собственных значения, причём одно из них нам уже известно: 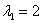 . Второе собственное число
. Второе собственное число 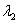 гипотетически тоже может равняться «двойке» (но чаще всего, и здесь – в частности, собственные значения различны).
гипотетически тоже может равняться «двойке» (но чаще всего, и здесь – в частности, собственные значения различны).
Могут ли собственные числа быть комплексными? Да, некоторые или все собственные значения могут быть комплексными. При этом алгоритм решения типовой задачи будет точно таким же. Однако на практике мне таких заданий не встречалось, поэтому в примерах данной статьи я ограничусь действительными собственными числами.
Что касается количества собственных векторов, то с ними ситуация занятнее. Любой вектор, который коллинеарен вектору 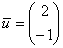 тоже будет собственным вектором. Действительно, если взять пропорциональные столбцы, скажем,
тоже будет собственным вектором. Действительно, если взять пропорциональные столбцы, скажем, 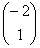 или
или 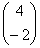 , то совсем несложно убедиться в равенствах:
, то совсем несложно убедиться в равенствах:
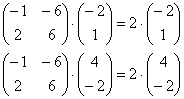
И с этой точки зрения у матрицы 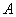 бесконечно много собственных векторов. Но ходить туда-сюда по одной и той же тропинке скучно и уныло, поэтому под рассматриваемым вопросом всегда подразумевают количество линейно независимых (неколлинеарных) собственных векторов.
бесконечно много собственных векторов. Но ходить туда-сюда по одной и той же тропинке скучно и уныло, поэтому под рассматриваемым вопросом всегда подразумевают количество линейно независимых (неколлинеарных) собственных векторов.
У квадратной матрицы размером 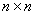 существует не более чем
существует не более чем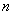 собственных векторов.
собственных векторов.
Например, матрица «два на два» обладает, как максимум, двумя собственными векторами. Однако стойкий оловянный солдатик может быть и в единственном экземпляре.
Каждому собственному значению соответствует хотя бы один собственный вектор, и из этого следует важное утверждение: если все собственные числа матрицы размером 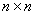 различны, то она имеет ровно
различны, то она имеет ровно 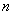 собственных векторов. И в первых примерах мы как раз угостимся этим винегретом:
собственных векторов. И в первых примерах мы как раз угостимся этим винегретом:
Date: 2015-07-23; view: 3960; Нарушение авторских прав