Как исследовать систему линейных уравнений на совместность?

Нередко помимо решения системы линейных уравнений по условию предварительно требуется исследовать её на совместность, то есть доказать, что какое-либо решение вообще существует. Ключевую роль в такой проверке играет теорема Кронекера-Капелли, которую я сформулирую в необходимом виде:

Если ранг матрицы системы равен рангу расширенной матрицы системы, то система совместна, причём, если данное число совпадает с количеством неизвестных, то решение единственно.

Таким образом, для исследования системы на совместность нужно проверить равенство 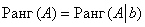, где 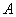– матрица системы (вспоминаем терминологию из урока Метод Гаусса), а 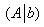– расширенная матрица системы (т.е. матрица с коэффициентами при переменных + столбец свободных членов).

Всё просто:

Пример 7

Исследовать систему на совместность и найти её решение, если система совместна

А когда системы уже прорешаны – просто вдвойне… нет – втройне =)

Решение: тем не менее, обратим внимание на строгую верхнюю строчку – по условию,
в первую очередь, требуется проверить систему на совместность. Как начать решение?
В любом случае записываем расширенную матрицу системы и с помощью элементарных преобразований приводим её к ступенчатому виду:

а) Пример №1 статьи о методе исключения неизвестных:

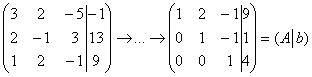
Элементарные преобразования не меняют ранга матриц, поэтому в результате выполненных действий получены эквивалентные исходным матрица системы 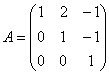и расширенная матрица системы .

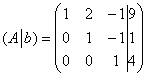Максимальный порядок ненулевого минора матрицы системы равен трём. Здесь таковой минор в единственном экземпляре и совпадает он, понятно, с определителем самой матрицы:
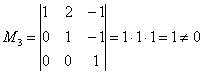(см. урок о методах вычисления определителя )

Следовательно, .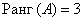

Максимальный порядок ненулевого минора расширенной матрицы системы также равен трём:
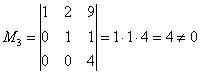(взяты первые два столбца + столбец свободных членов).

Таким образом, .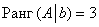

Вывод: 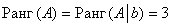, значит, по теореме Кронекера-Капелли система совместна; и поскольку количество переменных ( 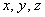– 3 шт.) совпадает с рангом, то система имеет единственное решение.

Что дальше? Дальше следует непосредственно решить систему. Если по условию не предложен способ, то, конечно же, раскручиваем обратный ход метода Гаусса. Если требуется решить систему методом Крамера или с помощью обратной матрицы, ну что поделать….

б) Пример №1 статьи о несовместных системах и системах с общим решением:

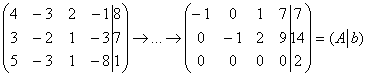
В результате элементарных преобразований получена эквивалентная матрица системы и расширенная матрица системы .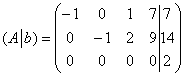

Максимальный порядок ненулевого минора матрицы системы равен двум, например:
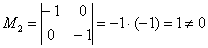, поэтому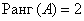

Заметьте, что здесь есть возможность выбрать и другой минор 2-го порядка, но проще всего в качестве примера взять ступенчатый определитель.

Максимальный порядок ненулевого минора расширенной матрицы системы равен трём, например:
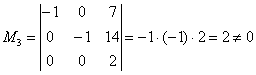(первые два столбца + столбец свободных членов).

Таким образом, .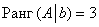

Вывод: , значит, по теореме Кронекера-Капелли система несовместна.

Однако помните – если по условию не требуется исследовать систему на совместность, то вполне достаточно ограничиться стандартным ответом (см. решение вышеуказанного урока).

в) Пример №3 той же статьи:

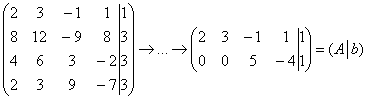
В результате элементарных преобразований получена эквивалентная матрица системы 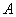и расширенная матрица системы .

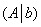Максимальный порядок ненулевого минора матрицы системы равен двум, например:
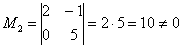, следовательно, .

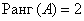Максимальный порядок ненулевого минора расширенной матрицы системы также равен двум, например:
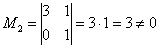, поэтому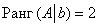

Второй абзац можно полностью заменить хитрой лаконичной фразой: «по этой же причине ».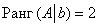

Вывод: 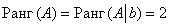, значит, по теореме Кронекера-Капелли система совместна. Поскольку ранг меньше количества переменных ( 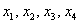– 4 шт.), то система имеет бесконечно много решений.

Далее находим общее решение по стандартной схеме.

Готово.

Образец исследования системы на совместность также можно посмотреть в начале
Примера №1 урока о нахождении различных базисных решений системы.

…Всё-таки иногда удивительно обманываются ожидания – порой думаешь, что статья получится огромной, а она оказывается весьма компактной, а иногда, как сейчас – наоборот. Посмотрел статистику и жутко удивился добрым 20-ти тысячам символов. Поэтому всем высокого ранга и до скорых встреч!

Решения и ответы:

Пример 2: Решение: поскольку в матрице есть ненулевые элементы, то её ранг не меньше единице.
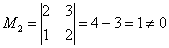, значит, ранг матрицы не менее двух.
Рассмотрим миноры 3-го порядка, при этом в них обязательно должен содержаться ненулевой минор 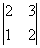. Таких миноров два:

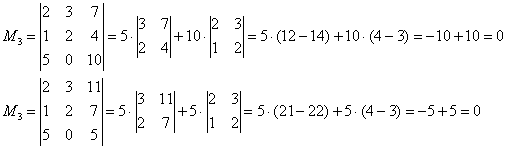
Максимальный порядок ненулевого минора равен двум.
Ответ: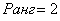

Пример 4: Решение: с помощью элементарных преобразований приведем матрицу к ступенчатому виду:

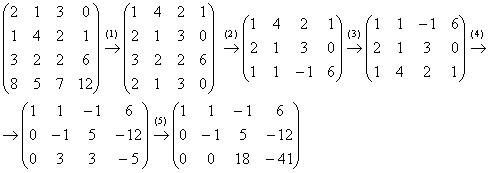
(1) Первую и вторую строки поменяли местами. К 4-ой строке прибавили 3-ю строку, умноженную на –2.
(2) Вторая и 4-ая строки одинаковы, 4-ю строку удалили. К третьей строке прибавили вторую строку, умноженную на –1.
(3) Первую и третью строки поменяли местами.
(4) Ко второй строке прибавили первую строку, умноженную на –2. К 3-ей строке прибавили первую строку, умноженную на –1.
(5) К третьей строке прибавили вторую строку, умноженную на 3.
В результате получены 3 строки, значит, ранг матрицы равен 3.
Ответ: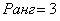

Пример 6: Решение: ранг матрицы не превосходит минимальной размерности, то есть, трёх.
В матрице есть ненулевые элементы, значит, ранг не менее единицы.

Максимальный порядок ненулевого минора равен трём
Ответ: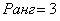

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Date: 2015-07-23; view: 3512; Нарушение авторских прав