Как найти ранг матрицы с помощью метода Гаусса?

Параграф рассчитан на читателей, которые уже знакомы с методом Гаусса и мало-мальски набили на нём руку.

С технической точки зрения метод не отличается новизной:

1) с помощью элементарных преобразований приводим матрицу к ступенчатому виду;

2) ранг матрицы равен количеству строк.

Совершенно понятно, что использование метода Гаусса не меняет ранга матрицы, и суть здесь предельно проста: согласно алгоритму, в ходе элементарных преобразований выявляются и удаляются все лишние пропорциональные (линейно зависимые) строки, в результате чего остаётся «сухой остаток» – максимальное количество линейно независимых строк.

Преобразуем старую знакомую матрицу с координатами трёх коллинеарных векторов:

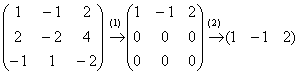
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку.

(2) Нулевые строки удаляем.

Таким образом, осталась одна строка, следовательно, 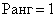. Что и говорить, это гораздо быстрее, чем рассчитать девять нулевых миноров 2-го порядка и только потом сделать вывод.

Напоминаю, что в самой по себе алгебраической матрице ничего менять нельзя, и преобразования выполняются только с целью выяснения ранга! Кстати, остановимся ещё раз на вопросе, почему нельзя? Исходная матрица несёт информацию, которая принципиально отлична от информации матрицы 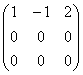и строки 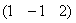. В некоторых математических моделях (без преувеличения) разница в одном числе может быть вопросом жизни и смерти. …Вспомнились школьные учителя математики начальных и средних классов, которые безжалостно срезали оценку на 1-2 балла за малейшую неточность или отклонение от алгоритма. И было жутко обидно, когда вместо, казалось бы, гарантированной «пятёрки» получалось «хорошо» или того хуже. Понимание пришло намного позже – а как иначе доверить человеку спутники, ядерные боеголовки и электростанции? Но вы не беспокойтесь, я не работаю в этих сферах =)

Перейдём к более содержательным заданиям, где помимо прочего познакомимся с важными вычислительными приёмами метода Гаусса:

Пример 3

Найти ранг матрицы с помощью элементарных преобразований

Решение: дана матрица «четыре на пять», значит, её ранг заведомо не превзойдёт 4-х.

В первом столбце, отсутствует 1 или –1, следовательно, необходимы дополнительные действия, направленные на получение хотя бы одной единицы. За всё время существования сайта мне неоднократно задавали вопрос: «Можно ли в ходе элементарных преобразований переставлять столбцы?». Вот здесь – переставили первый-второй столбец, и всё отлично! В большинстве задач, где используется метод Гаусса, столбцы действительно переставлять можно. НО НЕ НУЖНО. И дело даже не в возможной путанице с переменными, дело в том, что в классическом курсе обучения высшей математике данное действие традиционно не рассматривается, поэтому на такой реверанс посмотрят ОЧЕНЬ криво (а то и заставят всё переделывать).

Второй момент касается чисел. В ходе решения полезно руководствоваться следующим эмпирическим правилом: элементарные преобразования по возможности должны уменьшать числа матрицы. Ведь с единицей-двойкой-тройкой работать значительно легче, чем, например, с 23, 45 и 97. И первое действие направлено не только на получение единицы в первом столбце, но и на ликвидацию чисел 7 и 11.

Сначала полное решение, потом комментарии:

(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3. И до кучи: к 4-ой строке прибавили 1-ую строку, умноженную на –1.

(2) Последние три строки пропорциональны. Удалили 3-ю и 4-ую строки, вторую строку переместили на первое место.

(3) Ко второй строке прибавили первую строку, умноженную на –3.

В приведённой к ступенчатому виду матрице две строки.

Ответ: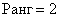

Теперь ваша очередь мучить матрицу «четыре на четыре»:

Пример 4

Найти ранг матрицы методом Гаусса

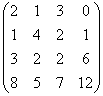
Напоминаю, что метод Гаусса не предполагает однозначной жёсткости, и ваше решение, скорее всего, будет отличаться от моего решения. Краткий образец оформления задачи в конце урока.

Date: 2015-07-23; view: 661; Нарушение авторских прав