Числовые характеристики случайных величин, их статистические и вероятностные значения. Центрированные случайные величины. Некоррелированные случайные величины

Полной характеристикой случайной величины является закон распределения. На практике такая характеристика не всегда может быть получена из-за ограниченности экспериментальных результатов. В этих случаях вместо законов распределения используют приближенное описание случайных величин, которая получается с помощью минимального числа неслучайных характеристик. Количество этих характеристик должно быть небольшим, но должно отражать наиболее существенные особенности распределении:

· математическое ожидание случайной величины;

· дисперсия (момент нулевого порядка, 1-го).

Простейшей числовой характеристикой дискретной случайной величины Х – среднее значени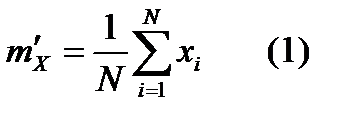е: , где 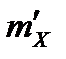- среднее значение случайной величины; N – число испытаний; 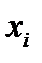- значение случайной величины, которое оно принимает при N испытаний.

Для характеристики разброса значений дискретной случайной величины в данной серии опытов используется квадрат разности между значениями случайно величины и её средним значением: 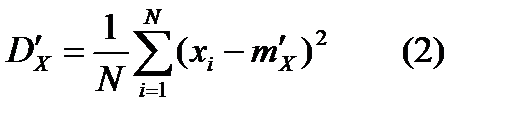, где 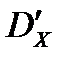- статистическая дисперсия случайно величины Х. При практических расчетах вместо дисперсии применяется среднеквадратическое отклонение: 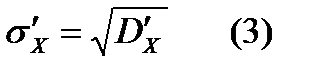, чем меньше 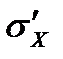, тем теснее группируются значения случайной величины около её среднего значения .

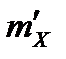Если результаты экспериментов характеризуются не одной случайной величиной, а несколькими, то кроме рассмотренных характеристик вводятся величины, характеризующие степень зависимости между этими случайными величинами. В качестве такой характеристики, например для 2-х случайных величин х и у в данной серии опытов принята величина: 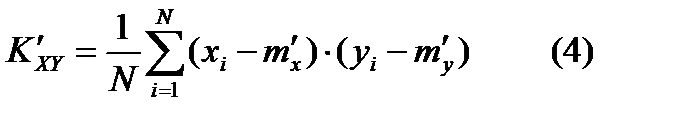. Равенство (4) статическим корреляционным моментом. При увеличении опытов значение частоты появления данного события 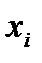будет приближаться к вероятности 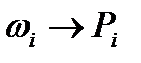. А среднее арифметическое значение 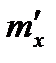будет стремится к её математическому ожиданию 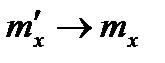: 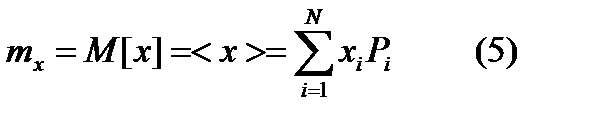, где 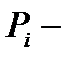вероятность появления значения 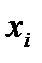. Таким образом, математическим ожиданием дискретной случайной величины Х называется сумма произведений всех её возможных значений х на вероятность появления этих значений 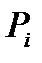. 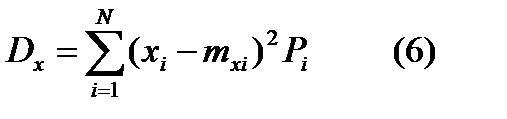, дисперсией случайной величины называется её математическое ожидание квадрата отклонения от этой величины от её математического ожидания. 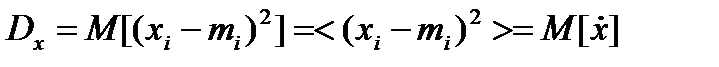, где 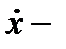центрированная случайная величина, 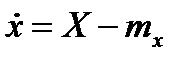, 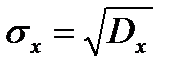. Корреляционный момент: 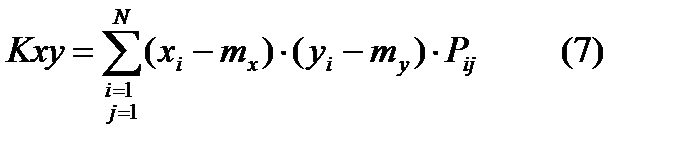, где - это вероятность того, что случайная величина х, у примут значения x_i, y_i, .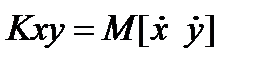

Для непрерывных случайных величин математическое ожидание, дисперсия и корреляционный момент определяются через плотность: .

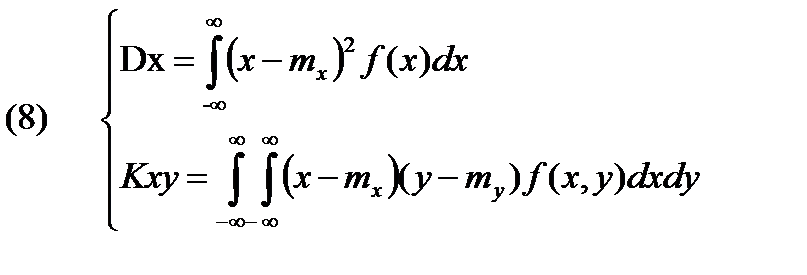
Для независимых случайных величин: 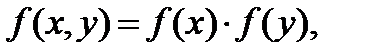тогда 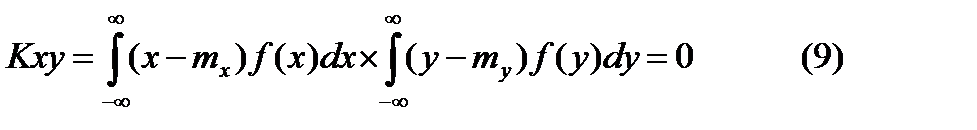, 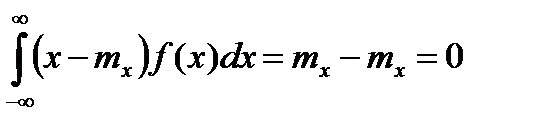. Согласно (9) для независимых случайных величин 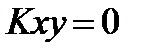потому, если 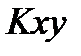двух случайных величин отличен от 0, то это указывает на наличие зависимости между этими случайными. Случайные величины для которых 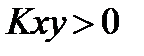называются некорреляционными случайными величинами. 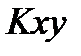характеризует не только зависимость величин, но и их рассеивание. Если, например, одна из величин Х или У мало отклоняется от своего математического ожидания, то корреляционный момент будет мал какой бы зависимостью эти величины мужду собой не обладали.

Для устранения этого недостатка вводится безразмерная характеристика, которая называется коэффициентом корреляции: 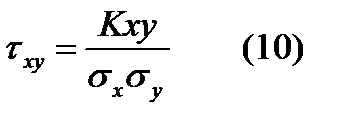. Если пользоваться механической интерпретацией, то абсциссу можно представить как центр тяжести фигуры, а дисперсию как момент инерции плоской фигуры.

Date: 2015-07-23; view: 908; Нарушение авторских прав