Функция распределения случайной величины

Основные понятия теории вероятностей. Теоремы сложения и умножения вероятностей. Условная вероятность события

Случайное событие – это такое событие, которое может произойти, может и не произойти при этом заранее не известно будет ли оно. Если же событие обязательно произойдет оно называется достоверным. Если оно не возможно оно будет недостоверным. Чтобы установить установит произойдет событие или нет необходимо проводить опыт. Опыт показывает, что при большем числе испытаний (при неизменных условиях опыта) они начинают подчинятся неслучайным законам. Эти законы называются вероятностными. Число появления событий при испытании характеризуется частотой события - .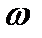

Частота события называется число в виде отношения числа испытания n, где данное событие произошло, к числу всех проведенных испытаний N. Это отношение справедливо при условии, что исходные событий в серии опытов независимы, т.е. если появление событий не влияет на появление других. При очень большом числе испытаний частота появлений событий 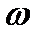начинает мало изменяться, приближаясь к некоторой величине Р (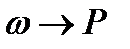), называемой вероятностью событий. Числовая характеристика случайного события, обладающая тем свойством, что для любой достаточно большой серии испытаний частота событий лишь отличается от этой характеристики называется вероятностью события 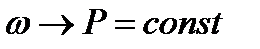. Если событие А повторяется большое число N раз, при этом в n случаях эти события обладают признаком В, а исходы событий независимы, то вероятность появления события В в виде: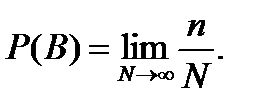

Зная вероятность события можно не проводить опытов и предсказать с какой вероятностью это событие будет появляться при большом числе опытов.

Вероятность событий представляют меру возможности появления события при одном опыте. Данное определение вероятности называется статистическим. Оно не является строгим с математической точки зрения.

Статистические определение вероятности позволяет установить:

· вероятность достоверного события (Р=1);

· вероятность невозможного события (Р=0);

· вероятность произвольного события А (0≤Р(А)≤1).

Если имеются 2 события А и В, А не зависит от того произошло ли событие В или нет, то такие события называются независимыми. Событие А называется зависимым от В если вероятность события А меняется от того произошло ли событие В или нет. Вероятность события А вычисленная при условии что имело место событие В называется условной событию вероятности Р(А/В).

1. Теорема сложения вероятностей. Вероятность суммы 2-х независимых событий равна сумме вероятности этих событий: Р(А+В)=Р(А)+Р(В).

2. Теорема умножения вероятностей. Вероятность произведения (совмещения) равна вероятности события А на условную вероятность события В: Р(АВ)=Р(А)*Р(В/А), Р(АВ)=Р(В)*Р(А/В).

3. Вероятность совместного осуществления 2-независимых событий равна произведению этих событий. Р(АВ)=Р(А)*Р(В).

Случайной называется величина которая в результате опыта может принять, то или иное значение заранее неизвестное. Случайная величина может быть дискретной или непрерывной.

Функция распределения случайной величины

Случайная величина будет полностью определена если будет известно с какой вероятностью возможно появление каждого из принимаемых величиной значения.

Такое соответствие называется законом распределения дискретной случайной величины. Для непрерывной случайной величины под вероятностью событий понимают вероятность величины Х, где Х< х, где х – некоторая текущая переменная.

Р(Х< х). Тогда величина Р(Х< х) есть некоторая функция, которая называется функцией распределения F(x)= Р(Х< х). Функция распределения должна удовлетворять условию 0≤F(x)≤1.

Из определения функции следует, что ни при каких больших х функция не может быть больше 1.0. .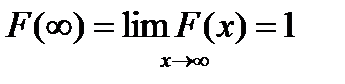

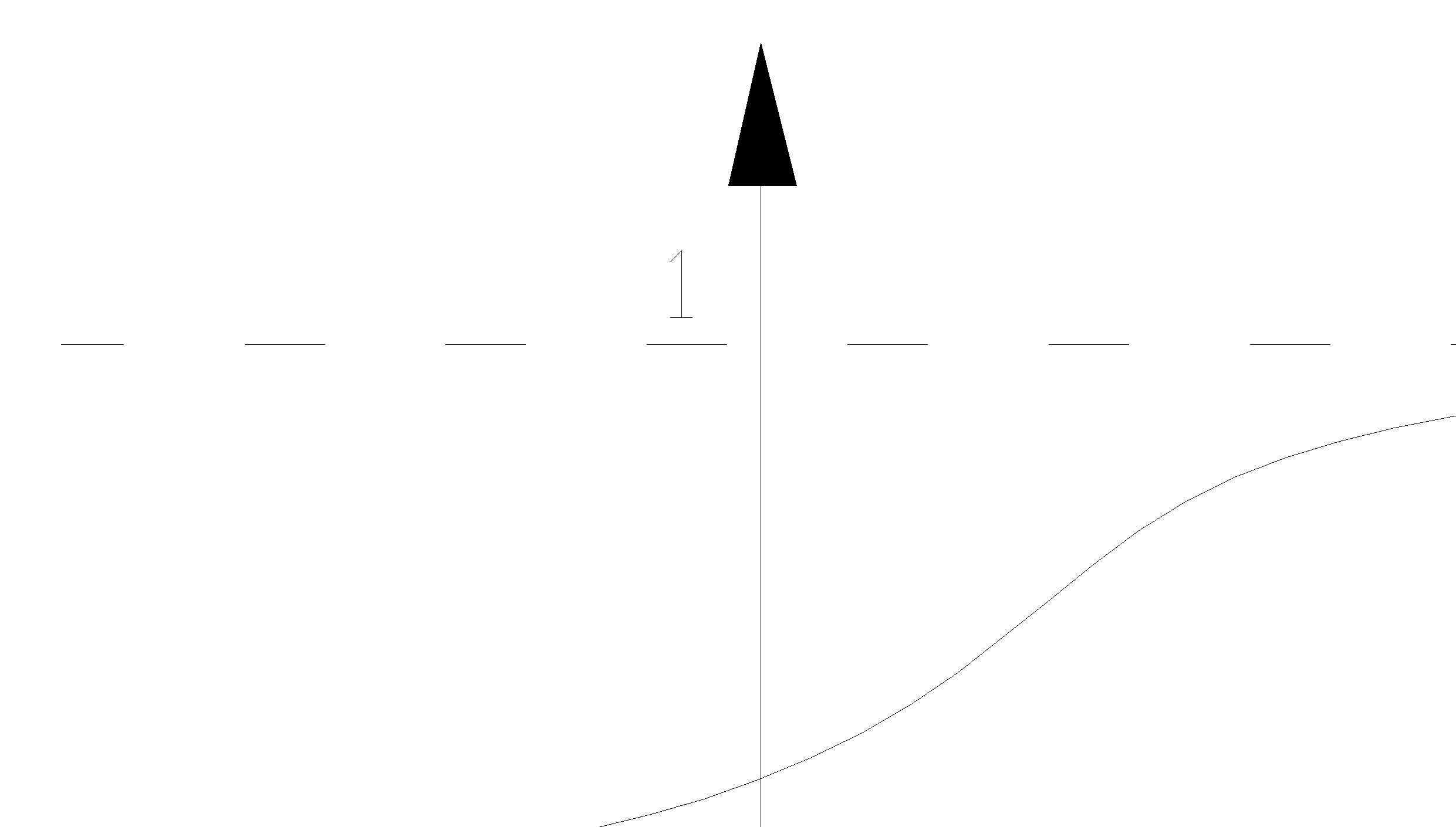Вероятность того, что случайная величина находится в интервале Х₁, Х₂: Р(х₁<Х<х₂)=F(x₂)-F(x₁). – это соотношение получается следующим образом: для выполнения неравенства необходимо и достаточно, чтобы величина Х лежала в пределах х₁≤Х≤х_2, т.к. событие Х<х₂ и Х<х₁ несовместимы, то согласно правилу сложения вероятностей:

Р(Х<х₂)=Р(Х<х₁)+Р(х₁<Х<х₂), Р(х₁<Х<х₂)=Р(Х<х₂)-Р(Х<х₁).

Date: 2015-07-23; view: 500; Нарушение авторских прав