
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Технич. сложность 5 page
|
|
| Часть 7. Философские проблемы математики И ФИЗИКИ | ||
| Тема 36. философский Образ математики как науки | ||
| 36.1. Математика как феномен человеческой культуры. | ||
| = Понимание значения математики | ||
| o Математика в Древних царствах | ||
| · формируется социальный заказ на применение арифметики, геометрии и алгебры | ||
| · математика техническое средство без доказательства | ||
| · рецептурная - инструкции на глиняных табличках для чиновников (счетоводы, землемеры) | ||
| o Античность: доказательная математика | ||
| · Смысл познания в античности | ||
| ü для познания явления необходимо «дать ему имя и число» | ||
| · В диалоге Платона «Филеб», объясняя собеседнику Протарху важность изучения музыкальных созвучий и образуемых ими систем, Сократ говорит | ||
| «...Предшественники наши, открывшие эти системы, завещали нам, своим потомкам, называть их гармониями и прилагать имена ритма и меры к другим подобным состояниям, присущим движениям тела, если измерять их числами; они повелели нам, далее, рассматривать таким же образом всякое вообще единство и множество... после того как ты узнаешь все это, ты станешь мудрым, а когда постигнешь всякое другое единство, рассматривая его таким же способом, то сделаешься сведущим и относительно него»1. Платон. Соч.: В 4 т. М., 1990-1994. Т. 3. С. 14. | ||
| · Пифагор «Все есть число» | ||
| ü научная программа поиска форм упорядоченности мира | ||
| o Новое время и современность | ||
| · Г. Галилей: «Книга природы написана на языке математики» | ||
| ü в исследовании движения тел приходит к необходимости применения математики и эксперимента | ||
| ü формулирует методы математического выражения движения | ||
| · НКН: | ||
| ü математика – средство познания ПиВ существования мира | ||
| · Всероссийская конференция «Математика и общество. Математическое образование на рубеже веков», 2000 г. | ||
| ü Доклад В.М. Тихомирова: | ||
| «Математическое образование есть благо, на которое имеет право любой человек, и обязанность общества (государства и всемирных структур) предоставить каждой личности возможность воспользоваться этим правом». | ||
| = Математика и естествознание | ||
| o Математика как система моделей | ||
| o Математика как язык науки | ||
| o Влияние методологии математики | ||
| · элементно-структурный подход | ||
| · формализация – замещение объектов (конструктивов) знаками | ||
| · оперирование знаками | ||
| · количественные методы | ||
| o Проблемы математизации естествознания | ||
| · элеаты, Платон | ||
| · Галилей, Декарт, Кант | ||
| = Математика и техника | ||
| o Теоретический уровень познания в технике | ||
| · целью ученого является приращение имеющихся в данной науке знаний. | ||
| · его деятельность исходит из наличного знания и завершается получением нового знания, что может быть выражено следующей схемой | ||
| понятие — дело — понятие | ||
| o Практическое познание в технике | ||
| · нацелено непосредственно на результат | ||
| · знания требуются лишь поскольку они способствуют достижению намеченного результата | ||
| дело — понятие — дело | ||
| 36.2. Взгляды на предмет математики | ||
| = Аспекты в истолковании предмета | ||
| «В философии науки принято различать три аспекта используемого в познавательной деятельности ученого языка науки: синтаксический, семантический и прагматический». Степин B.C. Теоретическое знание. М., 2003. С. 102—104. | ||
| o синтаксический | ||
| · язык как некоторая совокупность знаков | ||
| ü преобразуются по определенным правилам | ||
| ü формируют в своих связях определенную систему. | ||
| · исследователь | ||
| ü отвлекается от смысла терминов языка | ||
| ü рассматривает термины только как знаки | ||
| · знаки образуют формулы, из которых выводятся другие формулы по правилам данной языковой системы. | ||
| o семантический | ||
| · требует обращения к содержанию языковых значений. | ||
| · предполагает нахождение идеальных объектов и их связей, которые образуют непосредственный смысл терминов и высказываний языка. | ||
| · математические объекты | ||
| ü в аксиоматически построенной геометрии под пирамидой понимается не мысленный образ расположенной в пространстве пирамиды, | ||
| ü а идеальный математический объект, вершины которого не имеют частей, ребра — ширины, а грани — толщины. | ||
| o прагматический | ||
| · отношение языка к социокультурной практике | ||
| ü языковые выражения рассматриваются в отношении к практической деятельности и социальному общению | ||
| ü учитывается особенность конкретной исторической эпохи. | ||
| · идеальные объекты и их корреляции | ||
| ü образуют область смыслов языковых выражений, | ||
| ü берутся в их отношении к социокультурной среде, породившей ту или иную «популяцию» научных знаний | ||
| = Особенности образования и функционирования математических абстракций | ||
| o отношение математики к действительности | ||
| · математический метод | ||
| ü математик должен «добровольно» ограничивать свою связь с внешним опытом только формулировкой исходных положений | ||
| ü математик не должен требовать впоследствии дополнительного подтверждения собственных предложений сравнением с действительностью | ||
| · естественнонаучный метод | ||
| ü в е/знании принят гипотетико-дедуктивный способа рассуждений | ||
| ü он обязательно завершается проверкой теоретических выводов экспериментом | ||
| o теоретико-множественная концепция строения математической теории | ||
| · математическая теория имеет дело с одним или несколькими множествами объектов, связанными между собой некоторыми отношениями. | ||
| · все формальные свойства этих объектов и отношений, необходимые для развития теории, фиксируются в виде аксиом, не затрагивающих конкретной природы самих объектов и отношений. | ||
| · теория может применяться к любой системе объектов с отношениями, удовлетворяющей положенной в ее основу системе аксиом | ||
| 36.3. Этапы становления аксиоматического метода | ||
| 1) Период содержательной аксиоматизации | ||
| o аксиомы описывают основные свойства, отношения и связи объектов из одной области объектов | ||
| o последние получают непосредственное определение до того, как задан список аксиом рассматриваемой теории | ||
| o используемые при доказательствах средства логики не получают какого-либо описания или уточнения | ||
| o пример: Евклид «Начал» | ||
| ПостулатыЕвклида представляют собой требования возможности осуществления построений с идеальными геометрическими объектами | ||
| «Допустим: 1. Что от всякой точки до всякой точки <можно> провести прямую линию. 2. И что ограниченную прямую можно непрерывно продолжить по прямой. 3. И что из всякого центра и всяким раствором <может быть> описан круг. 4. И что все прямые углы равны между собой. 5. И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные эти две прямые неограниченно встретятся с той стороны, где углы меньше двух прямых». | ||
| o содержательный характер геометрической аксиоматики был поставлен под сомнение в первой половине XIX в. в связи с построением Лобачевским, Бойяи и Гауссом неевклидовых геометрий. | ||
| o аксиомы оказались не абсолютными истинами, отрицание которых недопустимо, а гипотезами, истинность которых надо проверять опытным путем либо путем сведения к ранее установленным математическим истинам | ||
| 2) Период полуформальной аксиоматизации | ||
| o объекты не получают непосредственных определений. Их заменяют аксиомы, описывающие отношения и связи между основными объектами | ||
| o аксиомы и теоремы справедливы для различных множеств объектов, с одинаковой, описанной в аксиомах, структурой отношений и связей между объектами | ||
| o каждую такую область называют моделью или интерпретацией аксиоматизированной теории | ||
| o при доказательствах теорем используются средства традиционной логики | ||
| 3) Период формальной (теоретико-множественной) аксиоматизации | ||
| o формальные аксиоматики получаются | ||
| · из полуформальных аксиоматик | ||
| · при помощи формализации традиционной логики, содержательным образом используемой в первых двух видах аксиоматик | ||
| o разработаны для теорий, относящихся преимущественно к фундаменту теоретической математики | ||
| o теоретико-множественная концепция | ||
| · позволила систематизировать возможные математические теории | ||
| а)чистая алгебра | ||
| · определяется как наука о системах объектов | ||
| · в которых задано конечное число операций, | ||
| · применимых (каждая) к определенному конечному числу объектов системы | ||
| · производящих из них новый объект системы | ||
| в)анализ и геометрия | ||
| · предполагают «непрерывность» изучаемых пространств | ||
| · существенно требуют введения «предельных» отношений, связывающих бесконечное число объектов. | ||
| с) специальные математические теории | ||
| · аксиоматическое изложение какой-либо теории (например, теории вероятностей) | ||
| ü не начинают на пустом месте | ||
| ü пользуются ранее построенными теориями | ||
| · требует обращения именно к теории бесконечных множеств, а последняя сама нуждается в логическом обосновании | ||
| 4) Парадоксы теории бесконечных множеств | ||
| o парадокс Рассела (брадобрея) | ||
| · Пусть М — совокупность всех нормальных множеств, т.е. множеств, не включающих себя в качестве собственного элемента. | ||
| · Допустим, что М — само нормальное множество, тогда оно не содержит самого себя в качестве элемента и тем самым не может быть нормальным. | ||
| · Если, напротив, предположить, что М — ненормальное множество, то тогда оно должно входить в М, т.е. быть нормальным множеством | ||
| o Попытки устранения парадоксов из математики и ознаменовали рождение новой научной дисциплины — философии математики | ||
| 36.4. Философия математики | ||
| = Концептуальные проблемы ФМ: | ||
| o сущность математики | ||
| o предмет и методы математики | ||
| o место математики в науке и культуре | ||
| = Фундаменталистский подход в ФМ | ||
| o Суть подхода | ||
| · выяснение проблемы сущности математики, не зависящей от ее конкретных исторических состояний | ||
| · попытки редукции одних теоретических разделов математики к другим разделам и нахождения фундаментальных математических структур | ||
| o Исследуется природа математических объектов и их соотнесенность с | ||
| · миром природных объектов | ||
| · объектами теоретического естествознания | ||
| o Поиск единой сущности и непреходящих стандартов математического доказательства — стандартов, с которыми сравниваются реальные доказательства различных эпох | ||
| = Нефундаменталистский (социокультурный) подход в ФМ | ||
| o Предвидение будущего математики | ||
| · важная и актуальная проблема - анализ развития математики | ||
| · выявление закономерностей развития | ||
| o Законы функционирования математики | ||
| · проблемы сущности математики, независимой от ее развития, отодвигается на задний план | ||
| · широкий взгляд на математику, ее отношение с другими науками, место и значение в культуре | ||
| o Основные работы: | ||
| «Общая схема развития математики на примере истории доказательства важного результата топологии — теоремы Эйлера о многогранниках». И. Лакатос «Доказательства и опровержения. Как доказываются теоремы» | ||
| «Математика рассматривается как подразделение культуры в целом. Важным является понятие «культурного элемента» как набора убеждений, инструментов, ритуалов (в широком смысле слова) и т.п., принадлежащих некоторым образом объединенной группе людей. На этой основе он строит типологию исторического взаимодействия различных частей математики, которая существенно отличается от привычного ее разделения на специальные теоретические дисциплины» Р. Уайлдер «Математика как культурная система» | ||
| «Построение целостной и развернутой эмпирической концепции сущности и развития математического знания как представленного в деятельности коллективного субъекта — научного сообщества математиков» Ф. Китчер «Природа математического знания» | ||
| o Историческая ветвь | ||
| · полагает развитие науки некумулятивным | ||
| · применяет концепцию научных революций Т. Куна к математике | ||
| · идея исторического отбрасывания устаревших математических теорий | ||
| o Ветвь социальной детерминации | ||
| · зависимость содержания науки от | ||
| ü социальных взаимоотношений | ||
| ü региональных и национальных особенностей | ||
| · социально обусловленные виды математики: | ||
| ü «арийская математика» (Л. Бибербах), | ||
| ü «китайская математика» | ||
| ü «буржуазная математика» в ее противопоставление «пролетарской математике» | ||
| ü «европейская математика» и т.д. | ||
| o Ветвь культурной детерминации | ||
| · течение когнитивно-культурной детерминации, | ||
| ü формальные структуры, трансформирующиеся в исходные математические структуры конкретной исторической эпохи, считаются обусловленными формирующимися в данной культуре познавательными установками | ||
| · течение деятельностно-культурной детерминации | ||
| ü сущность культуры - социальные эстафеты действия | ||
| ü они обеспечивают облик математики, приемлемые способы действия с математическими объектами | ||
| ü объекты это роли соотношения обозначений, воспроизводящих себя в соответствии с принципами нормативных систем | ||
| Тема 37. КОНЦЕПЦИИ МАТЕМАТИКИ И ЗАКОНОМЕРНОСТЕЙ ЕЁ РАЗВИТИЯ | ||
| 37.1. Внутренние и внешние факторы развития математической теории | ||
| = Интернализм | ||
| o Апология «чистой» математики (Г. Харди) | ||
| o Национальные математические школы и особенности национальных математических традиций (Л. Бибербах) | ||
| o Концепция Ф. Китчера: эволюция математики как переход от исходной (примитивной) математической практики к последующим | ||
| = Экстернализм | ||
| o Б. Гессен о социальных корнях механики Ньютона. | ||
| o Математика как совокупность «культурных элементов» (Р. Уайлдер). | ||
| o Эстафеты в математике (М. Розов). | ||
| o Влияние потребностей и запросов других наук, техники на развитие математики. | ||
| 37.2. Концепции математики | ||
| 37.2.1. Пифагореизм | ||
| = Чувственный мир и космос | ||
| o В мире чувственных предметов и явлений царит случайность | ||
| o Высказываемое о чувственном мире, недостоверно, является только мнением | ||
| o Космос является идеальной основой мира, которая может быть понята только умозрительно, посредством самого разума | ||
| o Лишь утверждения математики, относящиеся к космосу, выступают подлинным знанием, обладающим истинностью и неопровержимостью | ||
| = Математика | ||
| o Математические утверждения опираются не на показания чувств, а на умозрение | ||
| o Разум способен непосредственно (без опоры на чувственный опыт) отражать глубинные законы мироздания | ||
| = «Все есть число» | ||
| o Всякая вещь содержит присущую ей меру, определенное гармоническое соединение частей, благодаря которому она и существует | ||
| o Вещь может быть познана в своей сущности только через раскрытие ее числа, ее внутренней пропорциональности. | ||
| = Число | ||
| o Число как причина вещей, как основа вещей и как способ их понимания | ||
| o Числовой мистицизм, числа как идеальная субстанция, определяющая его возникновение | ||
| o Пытались соединить значимые для них вещи с числами, которые раскрывали бы их природу. | ||
| o Ставили числа на место природных стихий, из которых исходили первые греческие философы | ||
| = Пифагорейская идеология и несоизмеримость величин, парадоксы Зенона | ||
| o При любом выборе единицы измерения найдутся величины неизмеримые и непредставимые отношением натуральных чисел, которые, таким образом, уже не могут быть поняты как соответствующие определенному числу | ||
| = Пифагореизм в сочинениях Платона | ||
| o в «Теэтете» и «Тимее» Бог-демиург строит мир, опираясь на идею пропорционального соотношения всех его частей | ||
| o Каждое из природных начал соединяется с одним из пяти правильных многогранников: огонь — с тетраэдром, земля — с гексаэдром, вода — с октаэдром, воздух — с икосаэдром. | ||
| o Космос как высшее совершенство имеет форму сферы | ||
| = Критика пифагореизма Аристотелем | ||
| o Ценит факты и логику больше, чем мифологические построения | ||
| o Критика пифагореизма, отношение пренебрежительное | ||
| o Пифагорейская философия ложна прежде всего потому, что она не раскрывает причин вещей | ||
| 37.2.2. Эмпиризм | ||
| = Эмпирическая концепция Аристотеля. | ||
| o первичность вещей, опыта перед числами | ||
| · математические предметы не существуют отдельно от вещей: они связаны с вещами и возникают как таковые из способности отвлечения | ||
| · человек воспринимает вещи во всем многообразии свойств, но для познания: | ||
| · отвлекается от них | ||
| · оставляет лишь некоторые из них | ||
| · исследует их как отдельно (самостоятельно) существующие | ||
| · вещи первичны перед математикой и определяют ее содержание | ||
| o объяснение строгости математического мышления | ||
| · строгость математического рассуждения объясняется простотой ее предмета. | ||
| · простота – следствие абстрактности, отсутствие разнородности качеств, которые присутствуют в физике и других, более конкретных науках. | ||
| · доказанное | ||
| ü в математике доказано навсегда, | ||
| ü в физике нет ни одного утверждения, которое не стояло бы перед опасностью пересмотра и корректировки. | ||
| · опыт | ||
| ü математика не использует никаких показаний опыта, | ||
| ü геометрия не обращается к опытному анализу пространственных отношений | ||
| · многие объекты математики, в принципе не могут быть поняты в качестве абстракций из опыта. | ||
| = Современные концепции эмпиризма: | ||
| o Ж. Пиаже | ||
| · операциональный подход к пониманию природы исходных математических понятий | ||
| · необходимо различать два вида опыта: физический и логико-математический | ||
| · ребенок рассматривает камешки и сравнивает их по цвету - физический опыт и абстракции | ||
| · при счете, он отвлекается от всех их физических качеств, кроме необходимых для того, чтобы переложить их из одной кучки в другую | ||
| · математические понятия сформировались не в физическом, а в логико-математическом или операциональном опыте, т.е. через наблюдение операциональной активности | ||
| · математика— это наука о реальных и мысленных операциях, её предмет определен структурой операционального опыта | ||
| o И. Лакатос | ||
| · работа «Доказательства и опровержения», ряд статей по философии математики | ||
| · методологический эмпиризм, он направлен на критику строгости математического доказательства и логического обоснования теорий | ||
| · идеально строгих доказательств не существует. Любое доказательство содержит систему скрытых допущений и предпосылок, которые могут оказаться ошибочными или противоречивыми | ||
| · принятые для данного времени критерии строгости не являются неизменными | ||
| = Недостатки эмпирического обоснования математики | ||
| 37.2.3. Априоризм | ||
| = Философские предпосылки априоризма. | ||
| o сформировался в XVII—XVIII вв. | ||
| o возвращение к пифагорейскому делению знания на чувственное и умопостигаемое | ||
| o математика объявляется принципиально внечувственным знанием, основанным на специфической интеллектуальной (чистой чувственной) интуиции | ||
| = Р. Декарт | ||
| o разделил все истины на | ||
| · вечные, данные в очевидной (внечувственной) необходимости | ||
| · чувственные, постигаемые на основе опыта | ||
| o математику понимал как знание | ||
| · радикально отличное от эмпирического знания | ||
| · полученное на основе внечувственной очевидности и несвязанное с опытом | ||
| = Г. Лейбниц | ||
| o обоснование априоризма и аналитичности математики | ||
| o исходные математические понятия и необходимые истины (математические и логические) | ||
| · являются аналитическими, т.е. строго выводимыми из некоторой системы простых тавтологических утверждений | ||
| · рассматриваются как истины самого разума, покоящиеся на очевидности, имеющей внеопытную природу | ||
| · отличаются от истин случайных, основанных на опыте | ||
| = И. Кант | ||
| o Аналитичность и синтетичность истин | ||
| · отказался от воззрения Лейбница на аналитичность необходимых истин. | ||
| · аналитичностью обладает только логика, остальные же виды априорных истин являются синтетическими | ||
| · синтетичность математики обусловлена наличием в нашем сознании чистой чувственности, чувственного, но неэмпирического созерцания | ||
| o Чувственное созерцание позволяет сформулировать положения | ||
| · априорные (независимые от опыта) | ||
| · и одновременно синтетические, не сводимые к тавтологиям типа А = А. | ||
| o Исходные представления | ||
| · исходные положения геометрии опираются на чистое представление о пространстве, | ||
| · истины арифметики опираются на чистое представление о времени. | ||
| · чистые представления пространства и времени определяют как состав исходных принципов (аксиом) математики, так и логику математического мышления. | ||
| o Самоочевидность математического доказательства - каждый его шаг может совершаться только на основе очевидного синтеза | ||
| o Математические объекты | ||
| · положение о конструктивном характере математических объектов | ||
| · объекты, непосредственно данные в чистом созерцании, | ||
| · объекты, данные только своим правилом конструирования. | ||
| Мы не можем созерцать тысячеугольник, говорит Кант, но мы имеем самоочевидную схему построения этой фигуры, и данное обстоятельство позволяет нам высказывать о ней истинные суждения, несмотря на отсутствие непосредственного зрительного образа этой фигуры. Современные философские проблемы … / Под общ. ред. В.В. Миронова. — М.: Гардарики, 2006, с. 45 | ||
| o Неевклидовы геометрии | ||
| · существенно поколебали априоризма Канта. | ||
| · показывали возможность существования математических теорий, не обладающих априорной и самоочевидной основой. | ||
| · их аксиоматика не является очевидной, она обладает лишь логической определенностью | ||
| · многие из них не обладают и конструктивностью в кантовском смысле | ||
| 27.2.3. Формалистский подход | ||
| = Зародился и оформился | ||
| o в конце XIX в. - начале XX в. | ||
| o в связи с осмыслением статуса неевклидовых геометрий и теории множеств | ||
| o в работах Г. Кантора, А. Пуанкаре и Д. Гильберта | ||
| = Основные положения | ||
| o математика не является наукой, исследующей аспекты реальности | ||
| · она представляет собой лишь метод логической трансляции опытного знания | ||
| · состоит из совокупности структур, пригодных для этой цели | ||
| o основным требованием к аксиомам математической теории является | ||
| · не их очевидность и не их связь с опытом, | ||
| · а их непротиворечивость, необходимая и достаточная для ее приложения к опытным наукам | ||
| o к математике неприменимо понятие истинности в смысле опытного подтверждения | ||
| · математическая теория не истинна и не ложна | ||
| · она становится таковой только после соединения ее понятий с понятиями опытных наук | ||
| o обоснование научной теории | ||
| · обоснование содержательной науки состоит в установлении ее истинности | ||
| · обоснование математической теории заключается только в доказательстве логической непротиворечивости ее аксиом | ||
| Проблема обоснования математической теории понимается с этой точки зрения как строгое доказательство ее непротиворечивости. Современные философские … / В.В. Миронова, с. 46. | ||
| 37.3. Этапы развития математики | ||
| = Практическая и теоретическая математика | ||
| o Практическая математика | ||
| · обслуживает хозяйственные операции, возникает во всех древних цивилизациях (древневавилонской, египетской, китайской, индийской и др.) на весьма ранних ступенях их развития | ||
| · первые известные шумерские тексты экономико-математического содержания относятся к третьему тысячелетию до н.э. | ||
| o Теоретическая математика | ||
| · доаксиоматическая форма | ||
| ü возникает в целом ряде древних цивилизаций (например, древневавилонской или китайской) | ||
| ü связана с фактором социального характера - становлением специального математического образования («математика школы») | ||
| · аксиоматическая ветвь математики | ||
| ü явление уникальное | ||
| ü своим рождением она обязана особой культурно-исторической ситуации, сложившейся в V в. до н.э. в Древней Греции | ||
| = Дотеоретическая математика | ||
| o разработка вычислительных процедур, относящихся к практической математике | ||
| o развитие математики определяется влиянием внешних, в первую очередь экономических, факторов | ||
| o закономерности развития математики определяются общими закономерностями социально-экономических изменений, специфических для той или иной цивилизации | ||
| = Доаксиоматическая теоретическая математика | ||
| o Тесное взаимодействие практически ориентированных вычислительных и теоретических методов | ||
| o Теоретические методы решения собственно математических проблем развиваются в системе образования | ||
| = Рождение аксиоматической теоретической математики | ||
| o Существенно изменило взаимоотношения практической и теоретической ветвей математики | ||
| o Временной период | ||
| · в Древней Греции этот период продолжался до IV в. до н.э. | ||
| · в других культурах — китайской, индийской и др. — до XVII—XIX вв., когда восточная математика была «поглощена» математикой европейской | ||
| а) относительно независимое развитие дисциплин практической и теоретической математики | ||
| · продолжался в Европе до середины XVII в. | ||
| · практическая математика достигала вершин, когда без нее невозможно было обойтись | ||
| ü например, в итальянских городах-государствах XV в. вследствие бурного развития торговли и банковского дела | ||
| ü обучали в рамках того ремесла, в котором эта математика применялась (землемерие, строительство, банковское дело и т.д.) | ||
| · неаксиоматическая ветвь теоретической математики | ||
| ü развивалась следуя потребностям образования | ||
| ü обучали в элитных учебных заведениях (Академии Платона, Лицее Аристотеля, средневековых университетах) | ||
| · аксиоматическая ветвь теоретической математики | ||
| ü с рождения (уже в пифагорейской школе) внимала философско-религиозным императивам современной ей эпохи | ||
| ü обучали также в элитных заведениях | ||
| в) математические модели физического мира и техники | ||
| · в XVII в. в теоретической математике появляются модели для количественного описания физического мира, а затем, с XIX в., и технических устройств | ||
| · вытеснение практической математики (как самостоятельной дисциплины) и ее превращение в прикладную математику, т.е. раздел, из которого черпаются модели для приложений | ||
| · «чистая» математика ориентируется на аксиоматико-дедуктивный метод | ||
| = Современный этап развития | ||
| o Стремительная смена технологий | ||
| · приводит к необходимости создания буквально «на ходу» новых адекватных методов анализа количественных параметров. | ||
| · классические математические модели не справляются с математическим обеспечением новых технологических процессов | ||
| o Кризис математического образования | ||
| o Критика идеи кумулятивного развития математики | ||
| o Проблемой становится обоснование стратегий роста математики, исходя из | ||
| · анализа ее исторического развития в целом и | ||
| · особенностей наблюдаемых кризисных явлений | ||
| 37.4. Проблема обоснования математики | ||
| = Суть проблемы обоснования | ||
| o Обоснование строгости (законченности) математических доказательств | ||
| · основные доказательства алгебры и элементарной геометрии безупречны, они образуют логически связанную систему положений | ||
| · рассуждение, доказывающее строгость какого-либо доказательства, само должно быть обосновано в своей строгости и т.д. | ||
| · мы должны получить заключение о строгости доказательства | ||
| ü не на основе математического доказательства, | ||
| ü а из некоторых содержательных соображений, обладающих полной надежностью | ||
| · подавляющее число логиков и философов сомневаются в совместимости этих требований | ||
| · Лакатос исходит из эмпирического взгляда на формирование математических понятий | ||
| ü понятия не свободны от интуиции опыта | ||
| ü интуиция несовершенна и может проявить себя в виде скрытых лемм или парадоксов на некотором этапе развития математической теории | ||
| ü проблема в прояснении природы элементарных очевидностей, что на сегодня не ясно | ||
| o Обоснование непротиворечивости математических теорий, составляющих фундамент математической науки, прежде всего арифметика и теория множеств | ||
| · сформулировать общие требования к математической теории, гарантирующие ее непротиворечивость | ||
| · три программы обоснования | ||
| ü логицизм | ||
| ü интуиционизм | ||
| ü формализм | ||
| = Проблема обоснования на стадиях развития | ||
| o Геометрическое обоснование алгебры в Античности. | ||
| o Проблема обоснования математического анализа в XVIII в. | ||
| o Поиски единой основы математики в рамках аксиоматического метода. | ||
| o Открытие парадоксов и становление современной проблемы обоснования математики | ||
| = Логицистский анализ математики | ||
| o Логицистская установка Г. Фреге и её трудности | ||
| · свести понятия математики к понятиям логики | ||
| · представить принципы математических теорий в качестве общезначимых логических истин | ||
| o К. Гедель «О неразрешимых предложениях "Principia Mathematica" и родственных систем» (1931) | ||
| · почти все математические теории, включая арифметику, если допустить их непротиворечивость, не являются полными | ||
| · они содержит положения, истинные при некоторой интерпретации, но логически недоказуемые в теории | ||
| · бесперспективность логицизма как программы обоснования математики. | ||
| = Интуицизм Л. Брауэра | ||
| o Логицистское обоснование математики | ||
| · задача редукции математики к исходным представлениям арифметики, | ||
| · которые рассматриваются в качестве необходимых и далее неразложимых интуиций сознания. | ||
| · праинтуиция - исходная база математического мышления. | ||
| o Конструкция как о единственно законный способ оправдания математического существования. | ||
| · правильными и безусловно строгими являются только конструктивные рассуждения, которые связывают любое утвердительное суждение об объекте с его предъявлением в качестве конструкции. | ||
| · понятие актуального бесконечного множества полностью исключалось из математики как противоречивое по своей сущности. | ||
| · все допустимые математические объекты должны быть построены на основе натуральных чисел и интуитивно ясных операций с ними | ||
| · однако основные понятия математического анализа и даже некоторые принципы алгебры не поддаются конструктивному представлению | ||
| = Гильбертово обоснование математики | ||
| o Специфика подхода | ||
| · заключение о непротиворечивости реальной математической теории предполагается вывести из непротиворечивости ее формализованного аналога | ||
| · формалистское обоснование покоится на допущении, что непротиворечивость формализма, будучи доказанной, гарантирует полную надежность содержательной теории | ||
| o Строгость математики может быть достигнута только через | ||
| · уточнение ее языка | ||
| · прояснение логической структуры теории | ||
| o Понятие финитизма. | ||
| · истинность математического суждения относительно бесконечного множества предметов не может быть проверена | ||
| · строгая альтернатива, выражаемая законом исключенного третьего, не может быть применена к нему в качестве безусловной истины | ||
| · принцип финитизма - оперирование с бесконечным может быть сделано надежным только через конечное | ||
| o Формализация теории | ||
| · заключается в представлении ее аксиом в виде не имеющих содержания строчек символов | ||
| · представляет собой редукцию всех типов математической очевидности к предметной и логической очевидности | ||
| · предполагается наличие содержательной метатеории, которая включает в себя | ||
| ü описание структуры формализма, | ||
| ü общие принципы логики | ||
| ü специальные правила преобразования (принцип индукции и т.п.), допустимые для действий в рамках формализованной теории | ||
| o Обоснование непротиворечивости формализма должно состоять в доказательстве того факта, что | ||
| · в его рамках в соответствии с правилами логики и правилами введения производных объектов | ||
| · не может быть получено выражение, имеющее вид «0 = 1» | ||
| o Принципы гильбертовского финитизма (требования к метатеории), метатеория: | ||
| · является | ||
| ü синтаксической в том смысле, что она имеет дело только со знаковой структурой теории и с преобразованиями, допустимыми в этой структуре | ||
| ü содержательной, поскольку она относится к конкретному формализму как к своему единственному предмету | ||
| ü финитной, ибо она не имеет дела с операциями с бесконечными множествами и допущением актуальной бесконечности; | ||
| ü конструктивной: всякое утверждение о существовании объекта в ее рамках должно быть подтверждено процедурой его построения | ||
| · должна | ||
| ü быть способной доказывать непротиворечивость формализованных и соответствующих им содержательных теорий, независимо от их содержания | ||
| ü включать в себя только математически определенные понятия (принципа отделения оснований от философии) | ||
| o Теоремы К. Геделя и программа Д. Гильберта: современные дискуссии | ||
| · программа Гильберта была поставлена под сомнение теоремой Гёделя о непротиворечивости | ||
| · привел к устойчивому скептицизму относительно возможностей разрешения этой проблемы вообще | ||
| · убеждение в непротиворечивости математических теорий базируется исключительно на практике их использования, которая подтверждает их достаточную надежность в различных областях науки и техники. | ||
| · необходимо признать, что математика, как и другие науки, обосновывается в конечном итоге только из опыта и не имеет никаких оснований для утверждения своей полной надежности | ||
| = Общие выводы о состоянии и перспективах обоснования математики: | ||
| o Проблема обоснования математики в настоящее время пока не может считаться решенной ни в положительном, ни в отрицательном смысле | ||
| o Есть все основания полагать, что возможности ее положительного решения не так ограничены, как это представляют себе скептики, опирающиеся исключительно на факт провала традиционных программ обоснования. | ||
| o У нас нет абсолютных запретов на появление других более успешных программ, которые будут исходить из более адекватных представлений о природе математического мышления и об условиях его строгости. | ||
| o Мы должны хорошо осознавать, что наше продвижение к строгому обоснованию математики зависит от нашего понимания природы математического мышления, которое находится в процессе постоянного совершенствования | ||
| 37.5. Проблемы математизации науки | ||
| = Суть процесса математизации | ||
| o приложение математики к нематематическим наукам | ||
| · математика применяется к тем областям знания, которые достигли достаточно высокой степени структуризации своего объекта. | ||
| · далеко не все науки способны к ясной структуризации предмета, обеспечивающей использование математического метода | ||
| o интерпретация математической теории через понятия теории содержательной | ||
| o выявление математических связей и отношений, отражающих определенные аспекты реальности, зафиксированные в содержательной теории | ||
| = Способы математизации | ||
| o Метрические | ||
| · функциональные модели описывают на аналитическом языке некоторые стороны функционирования реальных систем | ||
| ü дифференциальный и интегральный анализ | ||
| ü новейший функциональный анализ | ||
| ü вероятностно-статистические методы исследования | ||
| ü математическая теории информации | ||
| ü теория игр | ||
| ü теория принятия решений | ||
| o Неметрические | ||
| · позволяют исследовать разнообразные структурные характеристики и отношения систем. | ||
| · методы: | ||
| ü проективная геометрия | ||
| ü теория групп | ||
| ü топология | ||
| ü теория множеств | ||
| = Полная математизация теории | ||
| o качественные характеристики объектов теории допускают адекватную меру | ||
| o все основные понятия и принципы теории поддаются выражению в математических понятиях | ||
| o математическая теория позволяет осуществить достаточно точные предсказания в области действия (приложения) этой теории | ||
| = Основная проблема и задачи математизации | ||
| o раскрытие онтологической основы математизации | ||
| o сложность предмета науки | ||
| o выяснение условий, обусловливающих возможность математизации | ||
| o установление требований, позволяющих понять возможную сферу эффективности математического метода | ||
| = Математические методы и формирование научного знания. | ||
| o Практическая математика | ||
| · предметом вычислительных процедур являются количественные характеристики вещей, вовлеченных в общественную практику. | ||
| · возникая из практики, именно в ней находит свое применение и в конечном итоге — оправдание своего существования. | ||
| o Теоретическая математика | ||
| · целью математических методов является решение задач, прямо не связанных с практикой, но возникающих в сфере самой математики | ||
| · два подуровня теоретической математики: | ||
| 1) не связанный с аксиоматизацией; | ||
| 2) опирающаяся на аксиоматико-дедуктивный метод, объекты носят идеальный характер | ||
| = Прикладная математика | ||
| o Логика и особенности приложений математики. | ||
| · главное - эффективность количественных методов при решении тех или иных конкретных специальных задач | ||
| · ценность метода подсчета совершенно не зависит от степени его общности | ||
| o Математика как язык науки. | ||
| o Уровни математизации знания: | ||
| · количественная обработка экспериментальных данных, | ||
| · построение математических моделей индивидуальных явлений и процессов, | ||
| · создание математизированных теорий | ||
| = Специфика приложения математики в различных областях знания. | ||
| o Новые возможности применения математики, предлагаемые | ||
| · теорией категорий | ||
| · теорией катастроф | ||
| · теорией фракталов и др. | ||
| o Проблема поиска адекватного математического аппарата для создания новых приложений | ||
| = Перспективы математизации нефизических областей естествознания. | ||
| o Границы, трудности и перспективы математизации гуманитарного знания. | ||
| o Границы применимости вероятностно-статистических методов в научном познании. | ||
| Теама 38. Онтологические проблемы физики | ||
| 38.1. Онтология физического знания | ||
| = Понятие онтологии | ||
| o Наиболее общие сущности и категории сущего изучает онтология, учение о бытии как таковом | ||
| o В онтологии посредством ряда принципов эксплицируется картина исследуемой реальности | ||
| o Физика - лидер естествознания и физическая картина мира длительное время выполняла роль общенаучной картины мира | ||
| o Научная картина реальности является долговременной исследовательской программой | ||
| = Онтологический статус физической КМ | ||
| Обобщенная характеристика предмета исследования вводится... посредством представлений (1) о фундаментальных объектах, на которых полагаются построенными все другие объекты, изучаемые соответствующей наукой, (2) о типологии изучаемых объектов, (3) об общих закономерностях их взаимодействия, (4) о пространственно-временной структуре реальности» Степин B.C. Философская антропология и философия науки. М., 1992. С. 126. | ||
| Картина мира является основанием научных теорий, обеспечивает систематизацию знаний, «функционирует в качестве исследовательской программы, которая целенаправляет постановку задач как эмпирического, так и теоретического поиска и выбор средств их решения». Там же. С. 128 | ||
| = Эволюция НКМ | ||
| o Эволюция НКМ приводит к пересмотру ранее сложившихся представлений о действительности | ||
| o Изменение НКМ | ||
| · сложный процесс | ||
| · каждая из конкретно-исторических форм картин реальности | ||
| ü реализуется в целом ряде модификаций | ||
| ü выражающих основные этапы развития научных знаний | ||
| · новые представления о реальности | ||
| ü постепенно входят в КМ через конкуренцию ряда альтернативных исследовательских программ | ||
| 38.2. Механическая НКМ(2/2 XVII в.) | ||
| = Условия формирования НКМ | ||
| o борьба декартовской и ньютоновской концепций природы в рамках механической КМ | ||
| o НКМ сложилась при переходе от эпохи Возрождения к эпохе Нового времени. | ||
| = Философские принципы механистической (классической) КМ | ||
| o Материальное единство мира, | ||
| o Нет разделения на небесный и земной миры | ||
| o Принцип причинности и законосообразности природных процессов | ||
| o Концепция атомизма | ||
| Основные абстракции КМ: · «неделимая корпускула», · «мгновенное взаимодействие между телами по прямой, меняющее их состояние движения», · «абсолютные пространство и время» | ||
| Мир состоит из неделимых корпускул; их взаимодействие осуществляется как мгновенная передача сил по прямой; тела, образованные из корпускул, перемещаются в абсолютном пространстве с течением абсолютного времени | ||
| = Научные принципы МКМ | ||
| o Отказ от созерцательности | ||
| o Экспериментальное исследование природы | ||
| o Описанием законов природы на языке математики | ||
| o Концепция абсолютного ПиВ и их однородности | ||
| o Конструкты теоретической схемы | ||
| · «система материальных точек», · «сила», · «инерциальная система отсчета». | ||
| 38.3. Электромагнитная НКМ(4/4 XIX в.) | ||
| = В основе лежат идеи Р. Декарта (½ XVII в.): | ||
| o близкодействие | ||
| o теория вихрей | ||
| = Фарадей: ввел понятие поля и экспериментально его исследовал | ||
| К числу основных свойств, описывающих тела наряду с массой, стали добавлять характеристику - электрический заряд. Экспериментом показано, что между магнетизмом и электричеством существует прямая динамическая связь, объединил электричество и магнетизм в понятии электромагнитного поля | ||
| Экспериментально подтвердил, что электричество и магнетизм передаются в пространстве не мгновенно по прямой, а по линиям различной конфигурации от точки к точке. Эти линии, заполняя пространство вокруг зарядов и источников магнетизма, воздействовали на заряженные тела. Силы не могут существовать в отрыве от материи, линии сил необходимо связать с материей как особую субстанцию. | ||
| = Понятие эфира | ||
| o непрерывная механическая среда, заполняющая все пространство, | ||
| o неподвижная или частично увлекается в движение движущимися телами | ||
| o возмущения этой среды - электромагнитное поле. | ||
| o с эфиром как абсолютным пространством связана выделенная система отсчета | ||
| = Теория эл/м поля | ||
| o Дж. Максвелл – создал теорию как обобщение и развитие предыдущих эмпирических данных и теорий | ||
| o Герц: экспериментальное обнаружение поля, критический эксперимент | ||
| 38.4. Квантово-релятивистская НКМ(XX в.) | ||
| = Сущность неклассической научной революции: | ||
| o Человек вышел за пределы окна чувственного восприятия в область микро- и мега- миров | ||
| o Проявились ограниченности человека как субъекта познания, что потребовало создания новых познавательных подходов и принципов | ||
| = Рождение релятивистских представлений | ||
| o Отказ от абсолютного ПиВ как неподвижной «сцены», на которой разыгрывались физические явления | ||
| o Галилей: | ||
| · движение как состояние, | ||
| · характеристики движения, различающие его виды, рассчитываются, а не наблюдаются | ||
| · принципы инерции и относительности | ||
| o Эйнштейн: | ||
| · СТО: | ||
| ü отвергла «эфир» как особую среду и придала идее поля фундаментальный смысл | ||
| ü наблюдаемые свойства ПиВ зависят от выбора инерциальной системы отсчета | ||
| · ОТО: ПиВ зависят от распределения вещества | ||
| = Формирование квантово-волновых представлений | ||
| o Классические частицы и поля | ||
| · частицы - дискретные, локальные образования, им присуще конечное число степеней свободы. | ||
| · поля непрерывны в пространстве с бесконечным числом степеней свободы | ||
| o М. Планк: | ||
| · математическая гипотеза – квантование действия, | ||
| · ћ – постоянная, мера квантования | ||
| o А. Эйнштейн: | ||
| · свет поглощается и излучается порциями, квантами света | ||
| · квант светового (эл/м) поля - фотон | ||
| o Луи де Бройль: | ||
| o Гейзенберг: принцип неопределенности | ||
| · движение частиц в П стало невозможно представить как механическое движение макрообъекта | ||
| · частице нельзя приписать определенную координату, ее движение описывается волновой функцией, амплитудами волн вероятности. | ||
| · мы можем найти лишь вероятность нахождения частицы вблизи данной точки пространства | ||
| · взаимное соответствие: каждому полю соответствуют определенные частицы, а частицам — квантовые поля | ||
| o Н. Бор: принцип дополнительности | ||
| · описание реальности микромира требует создания специальной экспериментальной ситуации | ||
| · у микрообъектов будут проявляются, в зависимости от экспериментального окружения, волновые или корпускулярные свойства | ||
| · для описания противоречивой реальности требуется использовать совместно несовместимые ранее теории | ||
| 38.5. Синергетическая НКМ | ||
| = Современные представления о фундаментальных объектах и взаимодействиях | ||
| o Фермионы | ||
| · частицы, составляющие вещество (атомы, молекулы и т.д.) | ||
| · подчиняются статистике Ферми—Дирака | ||
| · принцип запрета Паули: | ||
| ü две тождественные частицы с полуцелым спином не могут одновременно находиться в одном состоянии | ||
| · спин (внутренний вращательный момент) - полуцелый | ||
| · примеры: электроны, протоны, нейтроны и др. | ||
| o Бозоны | ||
| · кванты полей | ||
| · подчиняются статистике Бозе—Эйнштейна | ||
| ü принцип запрета Паули не работает | ||
| ü в одном и том же состоянии может находиться любое количество бозе-частиц | ||
| · спин (внутренний вращательный момент) = 0, 1 | ||
| · примеры: фотоны, глюоны, хиггеровские бозоны, гравитоны | ||
| o Виртуальных частиц | ||
| · в процессе рождения ВЧ не выполняется закон сохранения энергии, неопределенность ΔЕ | ||
| · в силу ΔExΔt ≥ ћ ВЧ не может существовать во времени, находиться и наблюдаться актуально, лишь как флуктуации вакуума | ||
| o Взаимодействия | ||
| · Сильное: самое интенсивное, наиболее прочная связь нуклонов (протонов и нейтронов) в ядрах | ||
| · Электромагнитное: вз/д частиц с эл/м полем, меньше интенсивность, носитель - фотон — квант эл/м поля, нет массы покоя | ||
| · Слабое: превращение нейтрона в протон, электрон и антинейтрино, распад элементарных частиц, в т.ч. квазистабильных частиц, с временем жизни 10-6—10-14 с. | ||
| · Гравитационное: наиболее слабое, присуще абсолютно всем частицам. Радиус его действия (как и электромагнитного) не ограничен, решающее в крупномасштабном строении Вселенной. | ||
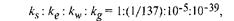 где ks — константа связи сильного взаимодействия,
ке — константа связи электромагнитного взаимодействия,
kw — константа связи слабого взаимодействия и
kg — константа связи гравитационного взаимодействия.
где ks — константа связи сильного взаимодействия,
ке — константа связи электромагнитного взаимодействия,
kw — константа связи слабого взаимодействия и
kg — константа связи гравитационного взаимодействия.
| ||
| Тема 39 Проблемы пространства и времени | ||
| 39.1. Исходные представления о ПиВ | ||
| = Понятие | ||
| o Атрибуты (способы существования) материи, характеризующие упорядоченность элементов и состояний в мире | ||
| o Функция понятий ПиВ: недопущение удвоения сущностей за счет различения | ||
| = Виды: | ||
| o Расстояние (отстояние в пространстве): | ||
| · различение рядом положенных (сосуществующих) объектов | ||
| · относительно, требует введения тела для отсчета (качество) и меры (количество) | ||
| o Перемещение | ||
| · изменение отстояния (расстояния) в пространстве | ||
| · объекты остаются самотождественными | ||
| o Длительность (во времени) | ||
| · различение последовательности тождественных состояний элементов/явлений | ||
| o Изменение (во времени) | ||
| · различение последовательности нетождественных состояний элемента/явления | ||
| = Основные свойства ПиВ | ||
| o Мерность пространства | ||
| · эмпирическое фундаментальное свойство - упорядоченности объектов в пространстве | ||
| · состояние объекта с n существенными свойствами в ПиВ точке м.б. представлено с помощью п независимых величин (степеней свободы) | ||
| · изменение свойства при математизации может представляться как пространственно-подобный параметр в обобщенном пространстве | ||
| · 3-х мерность макромира: механические перемещения имеют 3 степени свободы | ||
| · понятие п -мерного пространства - математическое обобщение при мысленном моделировании состояния объекта | ||
| o Необратимость, одномерность и однородность времени | ||
| o Однородность и изотропность пространства | ||
| · однородность означает равноправие всех точек, отсутствие каких-либо выделенных точек; | ||
| · изотропность — равноправие всех возможных направлений | ||
| o Инварианты – законы сохранения: | ||
| · теорема Нетер: если свойства системы не меняются от какого-либо преобразования переменных, то этому соответствует некоторый закон сохранения | ||
| · закон сохранения энергии - симметрии относительно сдвига времени (т.е. однородности времени) | ||
| · закон сохранения импульса - симметрии относительно пространственного сдвига (т.е. однородности пространства) | ||
| · закон сохранения момента импульса (углового момента) - симметрии относительно поворота координатных осей (т.е. изотропности пространства) | ||
| 39.2. Концепции ПиВ | ||
| = Субстанциальная концепции ПиВ | ||
| o ПиВ - нечто самостоятельно существующее наряду с материей, как ее пустые вместилища | ||
| o все объекты существуют в ПиВ, которые существуют самостоятельно и независимо от объектов | ||
| o пространство — это чистая протяженность, и время — чистая длительность, в которые как бы «погружены», «помещены» материальные объекты | ||
| o развитие и завершение субстанциальная концепция ПиВ получила у Ньютона и в классической физике | ||
| Демокрит: «...в действительности же существуют только атомы и пустота». Маковелъский А.О. Древнегреческие атомисты. Баку, 1946. С. 224. | ||
| = Реляционная концепции ПиВ. | ||
| Г. Лейбниц «Я вовсе не говорю, что материя и пространство одно и то же, а лишь утверждаю, что без материи нет и пространства и что пространство само по себе не представляет собой абсолютной реальности». Полемика Лейбница с Кларком. Л., 1960. С. 84. | ||
| «Пространство и время — общие формы координации материальных объектов и их состояний. Пространство — это совокупность отношений, выражающих координацию сосуществующих объектов, их расположение друг относительно друга и относительную величину (расстояния и ориентация); время — совокупность отношений, выражающих координацию сменяющих друг друга состояний (явлений), их последовательность и длительность». Физический энциклопедический словарь. М., 1965. Т. 4. | ||
| 39.3. Проблема ПиВ в классической механике | ||
| = Социальный заказ на науку Нового времени | ||
| o Социальное значение применения огнестрельного оружия (пушек) в конце средневековья | ||
| o Проблема теоретического объяснения полета ядра | ||
| · ненаглядность явления – выход за возможности органов чувств (окно чувственного восприятия) | ||
| · недостаточность физики Аристотеля для объяснения движения ядра | ||
| · необходимость различения и познания качественно различных видов движения | ||
| = Галилей: | ||
| o Постановка экспериментального исследования | ||
| · гипотеза о независимости естественного и вынужденного движений | ||
| · опыты со скатыванием ядра по наклонной плоскости | ||
| · исследование факторов: высота скатывания, масса ядра, шероховатость поверхности | ||
| · мысленный эксперимент: абсолютно гладкая поверхность, расстояние качения | ||
| o Рождение новых познавательных принципов: | ||
| · принцип инерции | ||
| · принцип относительности движения, | ||
| · новое понимание движения как состояния | ||
| · сила – причина изменения состояния движения | ||
| = Принцип относительности в кл. механике: | ||
| o Покоящиеся относительно друг друга с.о.: | ||
| · тела в одной системе, различие между ними - геометрический перенос начала координат | ||
| o Инерциальные с.о.: | ||
| · с.о. относительно друг друга движутся равномерно, прямолинейно | ||
| · принцип относительности утверждает физическую эквивалентность всех инерциальных систем отсчета | ||
| · переход от одной системы к другой не меняет вида второго закона Ньютона он остается справедливым | ||
| · состояние равномерного, прямолинейного движения не сказывается на происходящих в системе механических процессах и никакими механическими экспериментами, проводимыми внутри системы, нельзя определить, покоится она или движется равномерно и прямолинейно | ||
| · абсолютное пространство как инерциальная с.о. | ||
| o Неинерциальные с.о. – относительно друг друга движутся с ускорением | ||
| · при переходе от одной системы отсчета к другой появляются добавочные силы - силы инерции | ||
| = Преобразования Галилея и понятие ковариантности законов механики. | ||
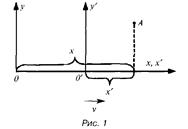
| х'=х — vt; z' = z, y' = y; t' = t. | |
| «В рамках классической механики абсолютные пространство и время стали чем-то неуловимым — физический эксперимент фактически ничего не мог о них сказать. В силу принципа относительности состояние равномерного прямолинейного движения неотличимо от состояния покоя, а значит, движение относительно абсолютного пространства нельзя обнаружить никакими механическими экспериментами». Современные философские проблемы … / Под общ. ред. Миронова. - М.: Гардарики, 2006, с. 102. | ||
| o Инвариантность — неизменность значений физических величин
Date: 2015-06-11; view: 483; Нарушение авторских прав |