Лекция 9. Задачи нелинейного программирования

Содержание лекционного занятия:

· Формулировка задач нелинейного программирования

· Классификация задач нелинейного программирования

Задачи математического программирования включают, прежде всего, задачи линейного и нелинейного программирования. В свою очередь по­следнее принято подразделять на выпуклое, квадратичное программиро­вание и многоэкстремальные задачи.

В общем случае задача нелинейного программирования может быть записана в следующем виде. Найти min F(x) при ограничениях:

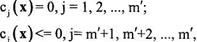
где х (х₁, х₂,..., х_n) — вектор из Е_n, F(x) — заданная це­левая функция, минимум которой предстоит найти, а c_j(x) — заданные скалярные функции, определяющие огра­ничения на область поиска. Дополнительно может присут­ствовать требование целочисленности всех или некоторых координат вектора х.

Эта формулировка универсальна в том смысле, что любая задача математического программирования может быть представлена в таком виде. В частности, при усло­вии линейности всех функций получаем задачу линейно­го программирования. Поскольку в этой формулировке никаких ограничений на вид или свойства функций зада­чи F(x) и Cj не накладывается, то разнообразие функций и их свойств предопределяет и разнообразие задач нели­нейного программирования. Эти функции могут быть или не быть непрерывными, иметь или не иметь частные про­изводные, быть или не быть выпуклыми, одноэкстремальными и т.д.

Универсального метода— такого как симплекс-метод для линейных задач — для решения нелинейных задач нет. С другой стороны, нет оснований считать каждую задачу уникальной, так как далеко не каждое изменение в форму­лировке задачи требует пересмотра метода ее решения. Другими словами, можно выделить классы задач и в пре­делах каждого класса — свои наиболее подходящие мето­ды решения.

Классификация задач проводится по различным при­знакам.

1. Наличие явных аналитических выражений функций за­дачи или только возможности их вычисления при кон­кретных значениях переменных путем решения допол­нительных подзадач.

2. Непрерывность функций и их производных (условия гладкости).

3. Наличие локальных экстремумов (многоэкстремальность).

4. Размерность задачи. От нее зависит, сколько памяти и времени вычислений требуется для решения задачи тем или иным методом. Как правило, методы, эффективные для задач с небольшим числом переменных, не пригод­ны при числе переменных в сотни и тысячи.

Дополнительно часто имеют значение «природа» зада­чи и внешние факторы. Например, некоторые ограничения должны быть выполнены с высокой точностью, а некото­рые могут выполняться с существенной допустимой по­грешностью (невязкой). Если результаты решения нужны как второстепенные данные для более общей задачи, то может оказаться бессмысленным поиск решения с мак­симальной точностью. Наконец, может требоваться толь­ко приближенное значение минимума, а сама точка, в которой он достигается, или вообще не нужна, или может быть найдена со значительными отклонениями по неко­торым переменным. Подобные ситуации возникают при оптимизации параметров отдельных подсистем в боль­ших системах.

Важное значение имеет конкретный вид функций. На­пример, система линейных ограничений может иметь структуру или соответствовать матрице, имеющей много нулевых элементов, что позволяет создать наиболее эффек­тивные алгоритмы как в рамках известных методов, так и новые методы оптимизации.

Вопросы для самоконтроля:

1.Нелинейное программирование. Основные определения и обозначения.

2.Постановка задачи нелинейного программирования.

3. Глобализация сходимости методов последовательного квадратичного программирования.

Рекомендуемая литература:

1.Ашманов С.А. Линейное программирование. —М.: Наука, 1981.

2.Айсагалиев А.С., Айсагалиева С.С. Лекции по методам оптмизации.-Алматы:Гылым,1996

Date: 2015-07-10; view: 1115; Нарушение авторских прав