Лекция 6. Двойственные задачи линейного программирования

Содержание лекционного занятия:

· Прямая задача

· Двойственная задача

Одним из центральных и наиболее значительных мест в теории линейного программирования является двойственность, которая состоит в том, что каждой исходной (прямой) задаче, в которой целевая функция стремится к максимуму (минимуму):

F = c₁,x₁,+с₂х₂+с₃х₃+... + с_nх_n ->max(min), (1)

система функциональных ограничений представляет собой систему неравенств:

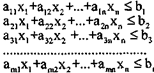(2)

система прямых ограничений также представляет собой систему неравенств:

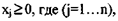(3)

соответствует двойственная задача, в которой:

· целевая функция стремится к минимуму (максимуму):

Z(y) = y₁,b₁, +y₂b₂+...+ y_mb_m -»min(max) (4)

· система функциональных ограничений, представляет собой систему неравенств:

(5)

• система прямых ограничений также представляет со­бой систему неравенств:

у₁³0,_У2³0,_Уз³0..._Уm³0. (6)

Общим для прямой и двойственной задач является то, что в каждой из них отыскивается экстремум линейной функции, а искомые переменные должны удовлетворять системам функциональных и прямых ограничений. Кроме того, в обеих задачах используются одни и те же парамет­ры: элементы матрицы А, вектор В, вектор С.

Отличие между прямой и двойственной задачей состоит в том, что в прямой задаче определяются значения n пере­менных x₁,x₂,...,x_n, а в двойственной — m переменных: y_1, y_2,…, y_m в исходной задаче ищется максимум, а в двой­ственной — минимум целевой функции, знаки неравенств в этих задачах противоположны, компоненты вектора огра­ничений в одной из задач являются коэффициентами при переменных в целевой функции другой задачи.

Чтобы к заданной прямой задаче сформировать двойст­венную, целесообразно пользоваться определенной систе­мой формальных правил.

1. Число переменных в двойственной задаче равно коли­честву функциональных ограничений в прямой задаче (т.е., если в прямой задаче вектор переменных записывается, как n-мерный вектор-столбец, то в двойственной задаче вектор переменных будет представлять собой m-мерный вектор — строку и наоборот).

2. Если прямая задача ставится как задача максимизации, то двойственная — как задача минимизации и наоборот.

3. Компоненты вектора функциональных ограничений В=(bi,b2,...b_m) в прямой задаче становятся коэффициентами целевой функции в двойственной задаче.

Применение этих трех правил позволяет сформировать целевую функцию двойственной задачи:

Z(y) = y₁ b₁ + у₂b₂ +...+ y_rab_m -> min.

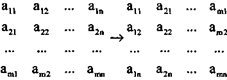
4. Матрица коэффициентов при переменных в системе функциональных ограничений двойственной задачи получается транспонированием матрицы коэффициентов при переменных в системе функциональных ограничений прямой задачи.

5. Знак неравенств функциональных ограничений в прямой задаче меняется на обратный в двойственной, т.е. «£» на «³».

6. Коэффициенты целевой функции прямой задачи c₁,c₂,...,c_n, становятся вектором ограничений в двойственной задаче.

Применяя правила 4, 6 мы можем сформировать систему функциональных ограничений обратной задачи:

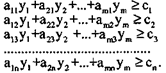
7. Прямые ограничения на неотрицательность перемен­ных для двойственной задачи сохраняются.

_У1³0,у₂³0,у₃³0...у_m³0

Таким образом, исходную и двойственную к ней задачу можно представить следующим образом:

Прямая и двойственная задача, построенная в соответствии с рассмотренными выше правилами, называются сим­метричными взаимодвойственными задачами.

Если к двойственной задаче снова построить двойствен­ную задачу, то получим прямую (т.е. исходную) задачу. Необходимо отметить, что ни одна из двойственных задач не является основной, так как если поставлена одна из за­дач, то другая может быть сформулирована как двойствен­ная и каждая из них является двойственной по отношению к другой.

Вопросы для самоконтроля:

1.Понятие о двойственных задачах ЛП.

2.Теорема двойственности.

Рекомендуемая литература:

1.Измаилов А.Ф., Солодов М.В. Численные методы оптимизации. М.: Физматлит, 2003.

2.Банди Б. Методы оптимизации. Вводный курс. М.: Радио и связь, 1988.

Лекция 7. Содержательная интерпретация прямой и двойст­венной задачи

Содержание лекционного занятия:

· Прямая задача

· Двойственная задача

· Основное неравенство теории двойственности

Прямая задача. Для изготовления n видов продукции предприятие ис­пользует m видов ресурсов, которые имеются на предприя­тии в количестве: b₁, b₂,..., b_m. При этом количество каждо­го из ресурсов i (i=l...m), которое идет на производство единицы продукции j-го вида (j=l...n), задается технологи­ческими коэффициентами а_ij. Выручка, получаемая пред­приятием от продажи единицы изготовленной продукции j-го вида (j=l...n), составляет соответственно c₁,c₂,...c_n. Не­обходимо составить такой план производства продукции X=(x₁,x₂,...x_n), при котором выручка предприятия от реали­зации всей продукции, изготовленной в соответствии с данным планом, будет максимальной, а количество каждо­го из ресурсов, используемых для выполнения заданного плана, не превысит имеющегося на предприятии запаса каждого из них.

Таким образом, в данной задаче:

• целевая функция: F = c₁x₁, + c₂x₂ + c₃x₃ +... + c_n x_n —» max отражает цель предприятия, которая заключается в макси­мизации выручки от продажи продукции, изготовленной в соответствии с оптимальным планом X=(x₁,x₂,...x_n);

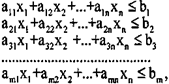
• каждое из неравенств, входящих в систему функцио­нальных ограничений:

отражает требования, предъявляемые к данному плану, ко­торые состоят в том, что количество каждого из видов ре­сурсов i (i=l...m), необходимых для производства каждого j-ro вида продукции (j=l...n) в количестве x_j, не должно превышать запасов b_j каждого из ресурсов, имеющихся на предприятии;

• каждое из неравенств, входящих в систему прямых ог­раничений: х1³0,х2³0,...,хn³0 отражает требования, состоящие в том, что количество каж­дого j-ro вида продукции (j=l...n) не может быть отрица­тельным.

Двойственная задача. Предположим, что то же предприятие, которое для про­изводства n видов продукции использует m видов ресурсов, при тех же самых технологических коэффициентах a_ij хочет минимизировать затраты на используемые ресурсы. Для этого ему необходимо найти такие оценки (цены) каждого из ресурсов — у_i (i=l...m), при которых затраты на них бы­ли бы минимальны, при этом искомые оценки (цены) ресурсов должны быть установлены таким образом, что за­траты на производство единицы продукции каждого j-ro вида не превышали бы выручки от ее реализации.

В данном случае под оценками (ценами) подразумева­ются объективно обусловленные оценки (понятие, впервые введенное Л. Канторовичем), которые, в отличие от цен, задаются не извне, а определяются самим предприятием для внутреннего пользования.

Таким образом, в данной задаче:

• целевая функция: Z(y) = y₁ b₁, + у₂b₂ +... + y_mb_m -> min отражает цель предприятия, которая заключается в мини­мизации затрат;

• каждое из неравенств, входящих в систему функцио­нальных ограничений:

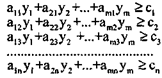
отражает требования, предъявляемые к искомым оценкам — y1, y2, …, ym которые выражаются в том, что затраты на производство единицы каждого j-го (j=l...n) вида продук­ции не превышают выручки от ее реализации (т.е. ее цены);

• каждое из неравенств, входящих в систему прямых ог­раничений: У1³0,у2³0,...,уm³0

отражает требования, предъявляемые к оценкам, которые заключаются в том, чтобы каждая из них — уi (i = l...m) должна быть неотрицательной.

Date: 2015-07-10; view: 1587; Нарушение авторских прав