Задачи с ограничениями-равенствами

Если линейная система ограничений содержит только ограничения-равенства, то задача записывается в следую­щем виде.

Найти: min F(x) при Ах = b, где А — заданная матрица (m ^х n), b — заданный вектор, а х — неизвестный вектор с координатами х_i (i = 1, 2,...,n). Относительно F(x) сохра­ним все те же предположения гладкости, что и в задачах безусловной оптимизации. Число строк матрицы А меньше числа ее столбцов (m < n) и строки предполагаются линейно независимыми, так как их линейная зависимость означала бы либо несовместность системы (отсутствие решений), либо наличие лишних ограничений, которые можно отбро­сить, не изменив решение задачи. Рассматриваемая нами задача может быть сведена к за­даче безусловной минимизации с помощью множителей Лагранжа. При этом ограничения исчезают, но для каждого из них вводится неизвестный множитель Лагранжа λ_i (i = 1, 2,..., m) и целевая функция приобретает вид:

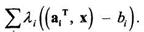
Здесь а_i, — i-ая строка матрицы А, так что ((a_i^T,x) – b_i) — это фактически левая часть i-oro ограничения-равенства, ес­ли систему переписать в виде Ах - b = 0. Конечно, как и при линейной целевой функции, можно было бы попытаться ис­ключить m переменных из системы и подставить их выраже­ния через оставшиеся переменные в целевую функцию. При этом уменьшилась бы размерность задачи и исчезли бы ограничения. Но для этого требуется большой объем вычис­лений, и нелинейная целевая функция не становится проще.

Введение множителей Лагранжа увеличивает число пе­ременных (их стало n + m), но дает возможность применить любой из методов безусловной минимизации.

Date: 2015-07-10; view: 472; Нарушение авторских прав