Лекция 8. Основные теоремы двойственности

Содержание лекционного занятия:

· Экономический смысл первой (основной) теоремы двойственности

· Вторая теорема двойственности

· Третья теорема двойственности

План производства X*=(x*₁,x*₂,..,x*_n) и набор объективно обусловленных оценок (по определению Л. Канторовича) ресурсов Y*=(y*₁,y*_2,…,y*m) оказываются оптимальными тогда и только тогда, когда выручка, полученная от произ­водства продукции, найденная при внешних сформирован­ных рынком, ценах: с₁ c₂,..,с_n на различные виды продукции предприятия равна его затратам на ресурсы в соответствии с объективно обусловленными оценками (внутренними цена­ми), которые устанавливает само предприятие на основании решения двойственной задачи.

Таким образом, из первой теоремы двойственности сле­дует, что предприятие имеет два равно выгодных для него варианта:

• первый из них предусматривает производство продук­ции в соответствии с оптимальным планом
X*=(x*₁,x*₂,..,x*_n) (определяемого на основании ре­шения исходной задачи) и получение максимально возможной выручки за выпущенную продукцию;

• второй вариант предусматривает для предприятия воз­можность получить ту же самую сумму средств, кото­рую дает максимальная выручка, но за счет продажи предприятием имеющихся у него ресурсов по ценам
Y*=(y*₁,y*_2,…,y*m), которые соответствуют двойст­венным оценкам, полученным на основании решения
двойственной задачи.

Из приведенного выше основного неравенства теории двойственности следует, что для других вариантов — пла­нов X и объективно обусловленных оценок У, которые не являются оптимальными, следует, что выручка от продажи продукции не превосходит (меньше либо равна) величины затрат на ресурсы.

Объективно обусловленные оценки определяют степень дефицитности ресурсов. Дефицитными оказываются те ре­сурсы, которые в соответствии с оптимальным планом про­изводства используются полностью и имеют ненулевые объективно обусловленные оценки, а недефицитные — ну­левые оценки. Другими словами, данный факт означает, что увеличение запаса недефицитных ресурсов не приведет к увеличению значения целевой функции.

Таким образом, в оптимальный план производства могут попасть только те виды продукции, рыночные цены кото­рых не превышают затраты на потребляемые при их изго­товлении ресурсы, а в точности равны им.

Прежде чем сформулировать следующую теорему, при­ведем как прямую, так и двойственную задачу к каноничес­кому виду и установим взаимосвязь между первоначаль­ными переменными одной из двойственных задач и допол­нительными переменными другой задачи.

Двойная система ограничений позволяет установить со­ответствие между первоначальными переменными одной из двойственных задач и дополнительными переменными другой задачи. Это соответствие представлено в таблице.

Теорема. Положительным (ненулевым) компонентам оптимального решения одной из взаимодвойственных задач соответствуют нулевые компоненты оптимального реше­ния другой задачи, т.е. для любых i=l...m, и j=l...n,

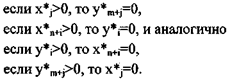
Вторая теорема двойственности. Компоненты опти­мального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих перемен­ных линейной функции исходной задачи, выраженной че­рез не основные компоненты ее оптимального решения.

Третья теорема двойственности. Компоненты опти­мального решения двойственной задачи равны значениям частных производных линейной функции F_max(b₁, b₂,...,b_m) по соответствующим аргументам, т.е.

dF_max/db_i=y*_i(i=l...m).

Из данной теоремы следует, что объективно обуслов­ленные оценки показывают, на сколько денежных единиц изменится максимальная выручка от реализации продукции при изменении запасов соответствующего 1-го ресурса на одну единицу.

В заключение необходимо отметить прикладное значе­ние двойственных оценок. Эти оценки могут быть исполь­зованы в качестве инструментария для принятия обосно­ванных решений в случае изменения объемов производства продукции, так как с помощью объективно обусловленных оценок ресурсов можно сопоставить оптимальные условия затрат и результатов производства (в случае небольшого изменения ресурсов).

Вопросы для самоконтроля:

1.В чем определяется неполнота оптимизационной модели.

2.Экономико- математический анализ полученных оптимальных решений.

Рекомендуемая литература:

1.Акулич И.Л. Математическое программирование в примерах и задачах. — М.: Высш. шк., 1986.

2.Алексеев В.М., Галеев Э.М., Тихомиров В.М. Сборник задач по оптимизации. М.: Наука, 1984.

Date: 2015-07-10; view: 866; Нарушение авторских прав