Градиентные методы. Градиентным методом называется метод, по которому на каждом шаге очередная точка определяется по формуле

Градиентным методом называется метод, по которому на каждом шаге очередная точка определяется по формуле

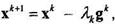(1)

т.е. направление спуска на каждой итерации - это анти­градиент, вычисленный в текущей точке х^к.

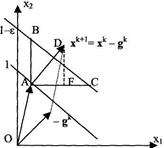
Рис. 4. Линии уровня и антиградиент

На рис. 4 текущему вектору х^к соответствует точка А. Примем за единицу значение целевой функции в этой точке и рассмотрим линию уровня со значением 1-ε, где ε доста­точно малая величина. При достаточно малом е эти линии уровня будем считать параллельными. Переход на линию уровня с меньшим значением при изменении только x₁ дает точку С, а при изменении только х₂ точку В. Обозначим расстояние АС через Δ₁,а АВ через Δ₂. Тогда для частных производных имеем приближенные равенства: дF/дх₁ = - ε /Δ₁ и дF/дх₂ = -ε/ Δ₂.

Градиентный метод, в котором на каждой итерации ис­пользуется шаг до точки минимума в направлении антиградиента, называется методом наискорейшего спуска.

Название наискорейший спуск не должно вводить в за­блуждение, так как оно вовсе не означает, что метод позво­ляет найти минимум за наименьшее число шагов по сравне­нию с другими методами.

Траектория спуска в этом методе носит зигзагообразный характер и градиенты в любых двух последовательных точ­ках ортогональны (рис. 6).

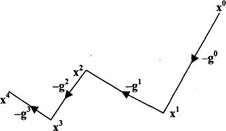
Рис. 6. Зигзагообразная траектория наискорейшего спуска