Лекция 4. Графический метод решения задач линейного программирования

Содержание лекционного занятия:

• ЗЛП имеет единственное решение
• ЗЛП имеет альтернативный оптимум
• ЗЛП имеет минимум и не имеет макси­мума
• ЗЛП не имеет решения

Графический метод решения задачи линейного про­граммирования имеет весьма ограниченную область при­менения. Как правило этим методом решаются задачи, со­держащие не более двух переменных.

Пример

Найти решение X*=(x*₁,x*₂), которое удовлетворяет системе неравенств:

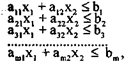
(1)

условиям неотрицательности переменных:
x₁³0, x₂³0, (2)

и которое доставляет оптимальное значение целевой функции:

f = c₁ x₁+с₂х₂ —»max(min). (3)

Необходимо отметить, что, несмотря на ограниченность применения, данный метод очень полезен для иллюстрации общих идей методов, используемых для решения задач ли­нейного программирования.

Применение геометрического метода предполагает ис­пользование нескольких этапов.

На первом из них в системе координат Х₁ ОХ₂ строится область допустимых решений задачи (ОДЗ). Для этого каждое из неравенств системы (1) заменяем равенст­вом и строим соответствующие этим равенствам гранич­ные прямые:

a _i1x₁+a_i2 x₂=b_i (i=l...m).

Каждая из этих прямых делит плоскость XiOX2 на две полуплоскости (рис. 1). Для точки (.) А, принадлежащей одной из этих полуплоскостей, выполняется неравенство:a _i1x₁+a_i2 x₂£b_i (i=l...m).

Для любой (.)В, принадлежащей другой полуплоскости, — противоположное неравенство: a _i1x₁+a_i2 x₂³b_i (i=l...m).

А для любой из точек, лежащих на граничной прямой, выполняется уравнение: a _i1x₁+a_i2 x₂=b_i (i=l...m).

решения, удовлетворяющие рассматриваемому нера­венству, достаточно испытать одну какую-либо точку, на­пример точку с координатами (0,0). Если при подстановке ее координат в левую часть неравенства оно удовлетворя­ется, значит, искомая полуплоскость содержит данную точ­ку и штриховка, выделяющая искомую полуплоскость, об­ращена в сторону к испытуемой точке.

Если же неравенство не удовлетворяется, штриховка, выделяющая искомую полуплоскость, обращена в проти­воположную от данной точки сторону.

Рис.1. Построение ОДЗ

Чтобы графически определить, по какую сторону от граничной прямой располагается полуплоскость, содержа­щая

Неравенства x₁³0, x₂³0, также соответствуют полу­плоскостям, одна из которых расположена справа от оси ординат, а другая - над осью абсцисс (рис. 1).

Выделив полуплоскости, содержащие решения, удовлетворяющие неравенствам, входящим в рассматри­ваемую систему, мы определим область, в которой нахо­дятся решения, удовлетворяющие всем ограничениям, входящим в рассматриваемую систему неравенств. Имен­но эта область и есть область допустимых решений зада­чи.

В общем случае область допустимых решений систем неравенств (1) и (2) может быть:

• пустой, что означает несовместимость систем нера­венств:

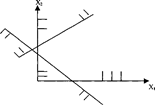
• одной точкой:

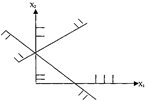
• выпуклым многоугольником:

• неограниченной выпуклой многоугольной областью:

Х₂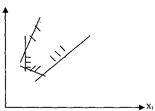

Рассмотренные примеры позволяют сделать следующий вывод: область допустимых решений системы неравенств может быть пустой, одной точкой, выпуклым много­угольником или неограниченной выпуклой многоуголь­ной областью.

На втором этапе формируется графическое изображение целевой функции.

Уравнение:

c₁ x₁+c₂x₂ =L при фиксированном значении L определяет прямую, а при изменении L — семейство параллельных прямых с параметром L. Вектор C=(c₁, c₂), перпендикулярный ко всем этим прямым, показывает направление возрас­тания параметра L. Так, на рис. 2 показаны прямые, соответствующие уравнению

2x₁+3x₂=L при L=-3, 0, 3, 9.

Рис.2. Графическое изображение целевой функции

Для всех точек, лежащих на одной из этих прямых, функция F принимает одно определенное значение, равное соответствующему значению L. Поэтому рассматриваемые прямые называются линиями уровня для параметра L.

Важное свойство линий уровня в том, что при их парал­лельном смещении в одном направлении уровень (значение L) только возрастает, а при смещении в другом — только убывает.

Построим, для рассмотренного выше примера линии уровня и определим направление их возрастания.

Чтобы построить вектор С=(с₁,с₂), можно использовать следующий прием: по оси X₁ откладывается значение пер­вой компоненты вектора с₁=2, а по оси Х₂ — значение вто­рой компоненты с₂=3.

По найденным координатам строим прямоугольник и находим направление возрастания вектора С. Затем пер­пендикулярно вектору С строим линии уровня.

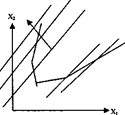
Построив на одном рисунке (рис. 3) область допус­тимых решений, вектор С, и перпендикулярную ему одну из линий уровня, можно путем ее параллельного переме­щения в направлении, указанном вектором С (или в проти­воположном), определить точку в области допустимых зна­чений, которая доставляет максимум или минимум целевой функции.

На рис. 3 видно, что в крайнем положении линия уровня проходит через (.) В. При дальнейшем ее перемеще­нии она уже не будет иметь общих точек с областью допус­тимых решений. Таким образом, искомое оптимальное ре­шение, которое графически соответствует координатам (.)В, можно найти путем совместного решения системы двух уравнений, соответствующих граничным прямым АВ иВД.

Если при тех же исходных данных требовалось бы до­стичь минимума функции F, то, очевидно, линию уровня пришлось бы перемещать в направлении, противоположном вектору С. В этом случае оптимальное решение, соот­ветствующее минимуму функции F, определялось бы коор­динатами точки (.) 0.

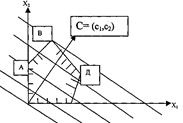
Рис. 3. Определение оптимального решения гра­фическим методом

В зависимости от вида области допустимых решений и положения линий уровня возможны следующие случаи:

• ЗЛП имеет единственное решение

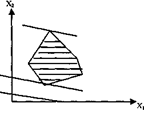
• ЗЛП имеет альтернативный оптимум

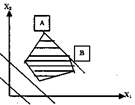
• ЗЛП имеет минимум и не имеет макси­мума

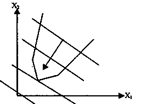
• ЗЛП не имеет решения

Вопросы для самоконтроля:

1.Геометрическое решение задач ЛП.

2. Элементы геометрии в n - мерном пространстве.

Рекомендуемая литература:

1.Ашманов С.А. Линейное программирование. —М.: Наука, 1981.

2.Айсагалиев А.С., Айсагалиева С.С. Лекции по методам оптмизации.-Алматы:Гылым,1996

Date: 2015-07-10; view: 1497; Нарушение авторских прав