
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Переход от стандартной формы задачам линейного программирования (ЗЛП) к канонической
|
|
Разнообразие форм задач линейного программирования затрудняет исследование их общих особенностей и создание общих методов и вычислительных алгоритмов для их решения. Поэтому естественно рассмотреть способ сведения любой задачи линейного программирования к наиболее простой и удобной для исследования форме — канонической.
Рассмотрим, каким образом можно перейти от стандартной форме записи к канонической. Для осуществления данного перехода нужно в каждое из m неравенств системы ограничений ввести m дополнительных неотрицательных переменных: хп+ь хп+2, хп+га, тогда система ограничений примет вид:
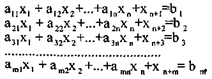
(4)
здесь xn+1, xn+2,...xn+m — выравнивающие балансовые переменные, где xj ³ 0, где (j = I...n+m). Добавив эти балансовые переменные в неравенства, превращаем их в уравнения.
Если же в стандартной форме требовалось минимизировать целевую функцию, то, заменив ее знак на «-», получим:
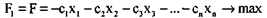 (5)
(5)
Таким образом, с помощью представленных преобразований мы перешли от стандартной формы ЗЛП к ее канонической форме.
Для решения этой задачи необходимо найти такой вектор Х=(х1, х2,x3,…,хn+m), который удовлетворял бы системе ограничений (4) и при котором целевая функция (5) принимала бы максимальное значение.
Пример
Пусть задача линейного программирования задана в стандартной форме: F = 2х, + Зх2 —> max при ограничениях:
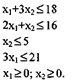
Приведем эту задачу к каноническому виду.
Обратим имеющуюся систему неравенств в равенства, водя для этого в каждое из них соответствующую неотрицательную переменную:
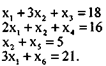
В данном примере все дополнительные переменные введены со знаком «+», так как рассматриваемые неравенства имеют знак £.
(Необходимо заметить, что в том случае, если неравенства имели бы знак ³, переменные нужно было бы вводить со знаком «-».)
Вопросы для самоконтроля:
1.Примеры задач линейного программирования (ЛП).
2.Формулировка общей задачи математического программирования.
Рекомендуемая литература:
1.Акулич И.Л. Математическое программирование в примерах и задачах. — М.: Высш. шк., 1986.
2.Алексеев В.М., Галеев Э.М., Тихомиров В.М. Сборник задач по оптимизации. М.: Наука, 1984.
Date: 2015-07-10; view: 2606; Нарушение авторских прав