Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Кольцо классов вычетов
|
|
Множество всех классов вычетов по модулю т обозначается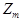 
или 
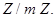Введем на этом множестве операции сложения классов и умножения классов.
Суммой классов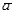 
и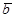 
называется класс 
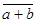т.е. класс, содержащий число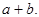 
Произведением классов 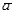и 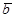называется класс 
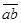, т.е. класс, содержащий число 
.
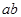Эти определения корректны, так как сумма любых двух представителей классов 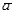и 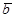всегда попадает в один и тот же класс, содержащий число 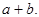Аналогичное утверждение имеет место и для произведения.
Действительно, если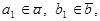 
то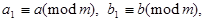 
следовательно, 
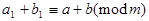и 
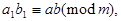т.е.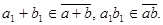 
Таким образом, определения суммы и произведения классов не зависят от выбора представителей классов.
Пример: Таблица сложения и умножения по модулю 6.
| + | ||||||
| x | ||||||
Теорема. Относительно введенных действий сложения и умножения классов множество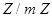 
– ассоциативное, коммутативное кольцо с 1.
Доказательство заключается в проверке аксиом кольца. ■
Теорема. Кольцо классов вычетов по простому модулю – поле.
Доказательство: Пусть р – простое число,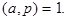 
Тогда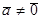 
и по теореме Ферма 
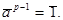Отсюда 
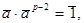т.е. обратным к классу 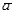является класс 
Мы получили, что любой ненулевой класс 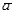в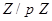 
имеет обратный, а это означает, что 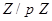– поле. ■
Date: 2015-07-02; view: 1788; Нарушение авторских прав