Полная система вычетов

Множество всех чисел, сравнимых с числом а по модулю т будем обозначать через 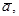т.е.

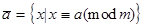
или

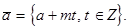
Это множество 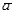называется классом вычетов числа а по модулю т. Легко видеть, что два класса вычетов либо не пересекаются, либо совпадают. Всем числам класса по определению соответствует один и тот же остаток при делении на т, следовательно, таких классов т штук. Взяв из каждого класса по одному представителю, получим полную систему представителей классов вычетов по модулю т. Любое число класса называется вычетом по модулю т по отношению ко всем числам того же класса.

В качестве примера полной системы представителей классов вычетов по модулю т (коротко: полная система вычетов) можно взять наименьшие неотрицательные вычеты 0, 1, 2,..., т -1. Можно взять наименьшие вычеты по абсолютной величине, т.е. в случае нечетного т числа

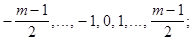
в случае четного т - какое-либо из двух множеств:

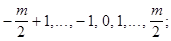
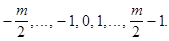
Теорема. Система вычетов по модулю т полна тогда и только тогда, когда в ней ровно т чисел, и числа попарно не сравнимы по модулю т. ■

Теорема. Если а и т взаимно просты и х пробегает полную систему вычетов по модулю т, то и 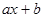пробегает также полную систему вычетов по модулю т; b – любое целое число.

Доказательство: Если х пробегает полную систему вычетов по модулю т, то принимает т значений, поэтому и чисел вида 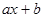получается т штук. Если 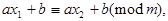то

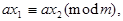
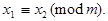
Отсюда следует, что есл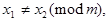и то и 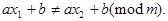Полученное множество содержит ровно т чисел, попарно несравнимых, т.е. является полной системой вычетов. ■

Date: 2015-07-02; view: 973; Нарушение авторских прав