Тригонометрическая форма комплексного числа. и комплексное число z можно выразить через его модуль и аргумент:

Пусть 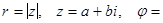Arg z. Тогда

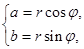
и комплексное число z можно выразить через его модуль и аргумент:

(тригонометрическая форма записи комплексного числа z).

Если z ₁ и z ₂ представить в тригонометрической форме:

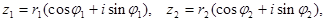
то

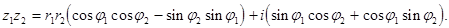
Используя формулы сложения синуса и косинуса, получим формулу умножения комплексных чисел в тригонометрической форме:

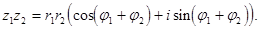
В правой части записано число в тригонометрической форме, модуль которого равен r ₁ r ₂, а аргумент 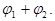Таким образом, 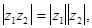Arg Arg 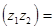z ₁ + Arg z ₂, т.е. при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Получается следующая геометрическая картина. Если z = z ₁ z ₂, то вектор получается из вектора 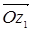поворотом его на угол 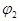против движения часовой стрелки, если 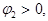и по движению в противном случае, и увеличением его в r ₂ раз. 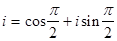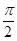Например, умножению числа z на отвечает поворот вектора на угол против направления движения часовой стрелки.

Рассмотрим деление комплексных чисел, записанных в тригонометрической форме:

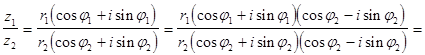
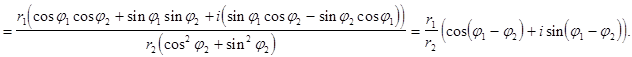
Следовательно,

Arg Arg z ₁ – Arg z ₂.

Иначе говоря, вектор для 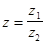получается из вектора 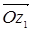поворотом его на угол 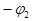и сокращением в r ₂ раз. Делению на i отвечает поворот на угол 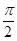по направлению движения часовой стрелки.

Замечание. Равенство Arg 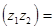Arg z ₁ + Arg z ₂ для главного аргумента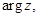 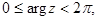вообще говоря, не верно. Его надо понимать в следующем смысле: для любых отличных от нуля комплексных чисел z ₁ и z ₂ среди всех возможных значений Arg z ₁, Arg z ₂ и Arg z ₁ z ₂ найдутся такие, для которых оно выполнено.

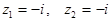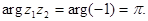Пример. Для имеем Но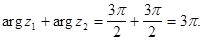

Пример. Записать в тригонометрической форме числа 1+ i;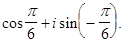

Решение: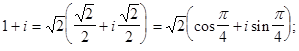

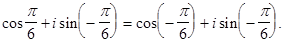
Date: 2015-07-02; view: 560; Нарушение авторских прав