Теорема Эйлера

Теорема. Если 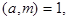то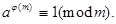

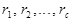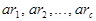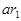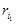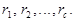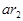Доказательство: Пусть числа образуют приведенную систему вычетов по модулю т. Тогда числа все взаимно просты с т и попарно не сравнимы по модулю т. Число попадает в один класс вычетов с каким-то из чисел Число попадает в один класс с другим числом 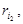но из этого же множества, т.е. имеем сравнения

......

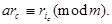
Здесь числа 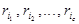- те же числа 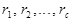, записанные, может быть, в другом порядке. Поэтому после перемножения сравнений можно записать

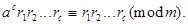
Откуда

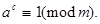
Что и требовалось доказать. ■

Малая теорема Ферма. Для любых целых чисел а и простого числа р

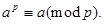
Доказательство: 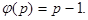Поэтому, если а не делится на р, то по теореме Эйлера

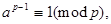
откуда следует, что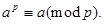

Если а делится на р, то 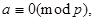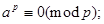откуда и получим сравнение ■

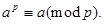Пример. Найти остаток от деления 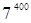на 101.

Решение: По малой теореме Ферма 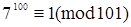, 101 – простое число; .

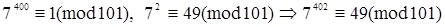Ответ: 49.

Пример. Доказать, что число 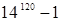делится на 45.

Решение: По теореме Эйлера 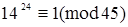. После возведения в пятую степень получим .

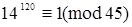Date: 2015-07-02; view: 834; Нарушение авторских прав