Поле центральних сил. Потенціальна і кінетична енергії

Усяке силове поле викликається дією деяких тел. Сила, що діє на частинку в такім полі, обумовлена взаємодією цієї частинки з даними тілами. Сили, що залежать тільки від відстані між взаємодіючими частинками і спрямовані по прямій, що проходить через ці частинки, називають центральними. Центральну силу, що діє на частинку М з боку частинки О, можна представити у вигляді: 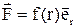, де f(r) – функція, що залежить при даному характері взаємодії тільки від г – відстані між частинками; 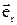– одиничний вектор, що задає напрямок радіуса-вектора частинки М щодо частинки О. Центральні сили є консервативними, тобто їхня робота не залежить від шляху, а визначається тільки початковим і кінцевим положенням тіла. По замкнутій траєкторії робота консервативних сил дорівнює нулю. Можна припустити, що робота консервативних сил є функцією радіуса-вектора точки: 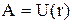. Функцію U(r) називають потенціальною енергією частинки в даному полі. Знайдемо роботу сил поля при переміщенні частинки з точки 1 у точку 2. Так як робота не залежить від шляху, виберемо шлях, що проходить через точку О. Тоді робота на шляху 1О2 може бути представлена у вигляді: А₁₂=А_1О+А_О2=А_1О–А_2О, або з урахуванням потенціальної енергії: А12=U1–U2.

З останньої формули випливає, що робота консервативних сил на шляху 1 – 2 дорівнює збитку потенціальної енергії частинки в даному полі. Отримане вираження дозволяє знайти потенціальну енергію для будь-якого стаціонарного поля консервативних сил:

- потенціальна енергія сили пружності:

;

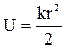- потенціальна енергія однорідної сили тяжіння:

;

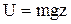- потенціальна енергія гравітаційного поля:

.

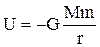Нехай частинка масою m рухається під дією деяких сил із прискоренням 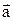. Визначимо роботу рівнодіючої сили по переміщенню точки. За формулою механічної роботи 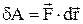. Так як і 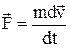, то після підстановки одержуємо:

.

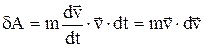Але

,

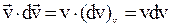де (dv)_v – проекція вектора dv на напрямок v. Ця проекція дорівнює збільшенню модуля вектора швидкості dv. У підсумку одержуємо: 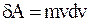. Повна робота сили при збільшенні швидкості точки від v₁ до v₂ дорівнює:

.

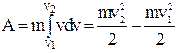Як видно з останньої формули, робота рівнодіючої сили дорівнює збільшенню деякої величини, яка називається кінетичною енергією.

Кінетичною енергією називається фізична величина, яка дорівнює половині добутку маси тіла на квадрат її швидкості:

.

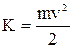Теорема про кінетичну енергію: Робота рівнодіючої сили, дорівнює зміні кінетичної енергії тіла:

.

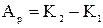Якщо частинки знаходяться в потенційному полі, то всі сили, що діють на неї можна розбити на консервативні і сторонні сили, що не мають відношення до даного поля. Таким чином, зміна кінетичної енергії дорівнює:

.

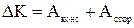Але робота консервативних сил дорівнює збитку потенціальної енергії:

.

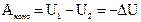Після відповідних підстановок одержуємо:

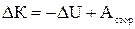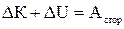, і .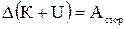

Суму кінетичної і потенціальної енергії називають повною механічною енергією частинки в поле:

.

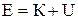Після заміни одержуємо:

.

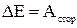Висновок: Збільшення повної механічної енергії частинки на деякому шляху дорівнює алгебраїчній сумі роботи усіх сторонніх сил, що діють на точку на цьому шляху.

Розглянемо систему з двох частинок 1 і 2. Визначимо алгебраїчну суму елементарних робіт сил F₁ і F₂, з якими ці частинки взаємодіють. Нехай у довільної К'- системі відліку за час dt частинки зробили переміщення 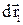і 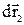. Тоді відповідна сума робіт цих сил

.

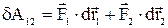За третім законом Ньютона 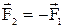. В підсумку отримаємо:

.

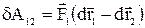Величина в дужках являє собою переміщення частинки 1 щодо частинки 2, точніше, переміщення частинки 1 у K'- системі відліку, жорстко зв'язаною з частинкою 2 і переміщається разом з нею поступально відносно К – системи відліку. Відповідно до закону додавання переміщень 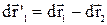і 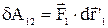. З отриманої формули випливає, що алгебраїчна сума елементарних робіт пари сил взаємодії в довільної K' – системі відліку дорівнює елементарній роботі, яку виконує сила, що діє на одну частинку, у системі відліку, де інша частинка спочиває. Інакше кажучи, робота 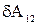не залежить від вибору вихідної К- системи відліку.

Сила 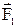, що діє на частинку 1 з боку частинки 2, є центральною, а отже і консервативною. Тому робота даної сили може бути представлена як збиток потенціальної енергії частинки 1 у поле частинки 2 чи як збиток потенціальної енергії взаємодії розглянутої пари частинок:

,

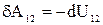де U₁₂ – функція, що залежить тільки від відстані між цими частинками. На всьому шляху 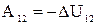. Якщо система складається з N частинок, то робота, що виконують усі сили взаємодії при переміщенні всіх частинок, може бути представлена як алгебраїчна сума робіт усіх пар сил взаємодій:

А =А₁₂ + А₂₃ + А₁₃+…

Але для кожної пари цих сил A_ik = –DU_ik, тому:

,

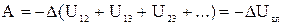де U_вл – власна потенційна енергія системи частинок: .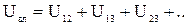

Так як кожен доданок цієї суми залежить від відстані між відповідними частинками, то очевидно, що власна потенційна енергія даної системи залежить від відносного розташування частинок, тобто від конфігурації системи. Кожній конфігурації системи частинок належить своє значення власної потенціальної енергії і робота усіх внутрішніх центральних консервативних сил при зміні цієї конфігурації дорівнює збитку власної потенціальної енергії системи:

.

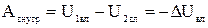Відповідно до теореми про кінетичну енергію, збільшення кінетичної енергії кожної частинки дорівнює роботі всіх сил, що діють на частинку. Тому роботу А, яку виконують усі сили, що діють на всі частинки системи при зміні її стану, можна записати так:

або

,

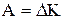де К – сумарна кінетична енергія системи.

Висновок: збільшення кінетичної енергії системи дорівнює роботі, яку виконують усі сили, що діють на всі частинки системи: .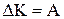

Власна механічна енергія системи частинок дорівнює алгебраїчній сумі кінетичної і власний потенціальної енергій системи:

.

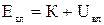Розділимо всі сили, що діють у системі, на зовнішні і внутрішні, а внутрішні на консервативні і дисипативні, Тоді теорему про кінетичну енергію можна переписати в такому вигляді:

.

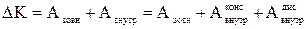Так як робота внутрішніх консервативних сил дорівнює збитку власної потенціальної енергії системи, останнє рівняння можна переписати у вигляді:

.

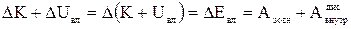Закон зміни повної механічної енергії системи тіл: Збільшення власної механічної енергії системи дорівнює алгебраїчній сумі робіт усіх зовнішніх сил і усіх внутрішніх дисипативних сил.

Date: 2015-07-01; view: 1150; Нарушение авторских прав