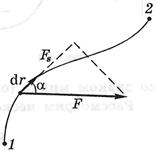
Теоретичні відомості. Нехай під дією сили частинка зробила переміщення по деякій траєкторії 1-2

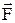Нехай під дією сили частинка зробила переміщення 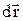по деякій траєкторії 1-2. Будемо вважати в межах переміщення 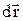силу постійною.

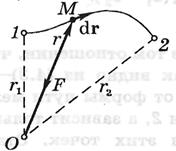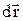Елементарною роботою сили по переміщенню називається фізична величина, яка дорівнює скалярному добутку сили 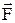на переміщення :

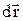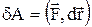
або

,

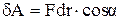де 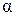– кут між векторами 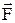і .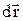

Робота – величина алгебраїчна, в залежності від кута 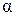вона може приймати позитивне значення, негативне чи бути рівною нулю. Проінтегрував вираження механічної роботи для ділянки 1-2, визначаємо роботу сили 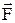на усій ділянці:

.

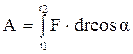Одиниці виміру механічної роботи в системі СІ: .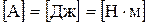

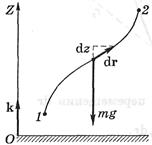
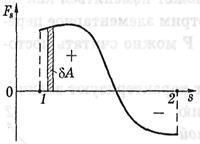Геометрична інтерпретація механічної роботи: Розглянемо графік проекції сили на напрямок 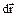як функцію положення частинки на траєкторії. З рисунку випливає, що елементарна робота dА чисельно дорівнює площі заштрихованої смужки, а робота А на шляху від точки 1 до точки 2 – площі фігури, обмеженої кривої, ординатами 1 і 2 і віссю s. При цьому площа фігури над віссю s береться зі знаком плюс (вона відповідає позитивній роботі), а площа фігури під віссю s – зі знаком мінус (вона відповідає негативній роботі).

Робота пружної сили. Згідно закону Гука

,

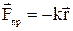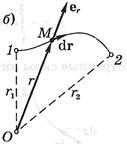
де 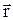– радіус-вектор частинки М щодо точки О.

Перемістимо частку М, на яку діє ця сила, по довільному шляху з точки 1 у точку 2. Елементарна робота на цьому шляху визначається з виразу:

.

Скалярний добуток

,

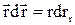де 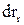– проекція вектора 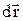на напрямок .

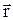У підсумку одержуємо:

.

Повна робота при переміщенні з 1 у 2:

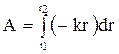або .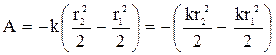

Date: 2015-07-01; view: 534; Нарушение авторских прав