Теоретичні відомості. Розглянемо довільну систему частинок

Розглянемо довільну систему частинок. Частинки системи можуть взаємодіяти як між собою, так і з тілами, що не входять у систему. Сили взаємодії між частинками системи називаються внутрішніми. Сили, які обумовлені дією тіл, що не входять у систему, називаються зовнішніми.

Імпульсом системи тіл називають векторну суму імпульсів окремих тіл, що входять у систему:

.

Знайдемо фізичну величину, що визначає зміну імпульсу системи тіл. Для цього продиференціюємо останню формулу за часом:

.

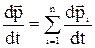Але за другим законом Ньютона

,

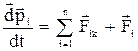де 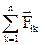– сума усіх внутрішніх сил, що діють на і-у частинку з боку інших частинок, 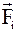– рівнодіюча зовнішніх сил, які діють на і-у частинку.

Підставивши останній вираз у попереднє рівняння, одержимо:

.

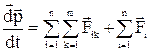Перший доданок в отриманій формулі – сума усіх внутрішніх сил. Але за третім законом Ньютона усі внутрішні сили однакові за модулем і протилежні за напрямком, тому рівнодіюча усіх внутрішніх сил дорівнює нулю:

.

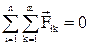В остаточному підсумку останній вираз приймає вигляд:

.

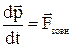Система частинок називається замкнутою, якщо на її не діють зовнішні сили або дія зовнішніх сил компенсується. З урахуванням останнього визначення одержуємо:

, .

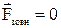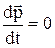
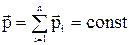Закон збереження імпульсу: Імпульс замкнутої системи частинок не змінюється при будь-якім переміщенні частинок усередині системи.

Замкнуту систему, у якій немає дисипативних сил, називають консервативною.

Закон збереження механічної енергії: У замкнутій системі при відсутності дисипативних сил повна механічна енергія не змінюється:

.

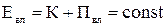Слід відзначити, що при русі замкнутої консервативної системи зберігається саме механічна енергія Е_вл, кінетична і потенційна в загальному випадку змінюються. Однак ці зміни відбуваються завжди так, що збільшення однієї з них у точності дорівнює збитку іншої:

.

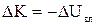Це положення справедливе тільки в інерціальних системах відліку. Якщо замкнута система не консервативна, то механічна енергія такої системи витрачається на роботу проти дисипативних сил, що діють у системі, тобто зменшується:

.

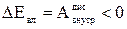Якщо система частинок знаходиться в зовнішньому стаціонарному полі консервативних сил, то зовнішні сили, що діють на частинки системи, можна розділити на сили з боку зовнішнього поля (зовнішні сили поля) і всі інші зовнішні сили, що не відносяться до даного зовнішнього поля (зовнішні сторонні сили). Відповідно робота зовнішніх сил може бути представлена як алгебраїчна сума робіт зовнішніх сил поля і зовнішніх сторонніх сил:

.

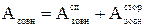Але робота зовнішніх сил поля дорівнює збитку зовнішньої потенціальної енергії:

.

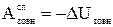Тоді вираз для роботи зовнішніх сил приймає вигляд:

.

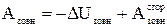Підставивши отримане рівняння у формулу для власної механічної енергії системи тіл, одержуємо:

.

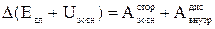Величину, що знаходиться ліворуч у дужках, називають повною механічною енергією Е системи в зовнішньому стаціонарному полі консервативних сил:

.

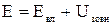На відміну від власної механічної енергії повна механічна енергія містить у собі крім сумарної кінетичної і власної потенціальної енергії ще і потенціальну енергію системи в зовнішньому полі 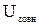. З урахуванням останнього визначення одержуємо:

.

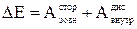З останнього рівняння випливає закон збереження повної механічної енергії системи, що знаходиться в зовнішньому стаціонарному полі консервативних сил: якщо на систему частинок не діють зовнішні сторонні сили і немає внутрішніх дисипативних сил, то повна механічна енергія системи не змінюється:

.

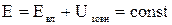Зв'язок між енергіями в К- і Ц-системах відліку. Нехай у К-системі відліку кінетична енергія системи частинок дорівнює К. Швидкість і-ї частинки можна визначити за формулою:

,

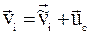де 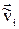– швидкість і-ї частинки в СВ, яка зв'язана з центром мас, 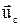– швидкість центра мас відносно К– системи. Тоді кінетична енергія системи може бути представлена в такому вигляді:

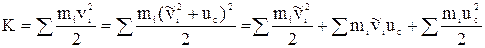
або

.

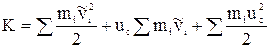Так як в Ц-системі центр мас не рухається, то

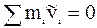
і попередній вираз приймає вигляд:

.

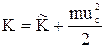Теорема Кёніга: Кінетична енергія системи частинок дорівнює сумі кінетичної енергії частинок у Ц-системі і кінетичній енергії, яка зв'язана з рухом Ц-системи.

Теорія пружних і непружних зіткнень. Непружним називають зіткнення, у результаті якого внутрішня енергія частинок, що розлітаються, змінюється, а отже, змінюється і сумарна кінетична енергія системи. Відповідне збільшення кінетичної енергії системи прийнято позначати Q. Абсолютно непружним називають зіткнення, у результаті якого обидві частинки "злипаються" і далі рухаються як єдине ціле. Нехай дві частинки, маси яких m₁ і m₂ мають до зіткнення швидкост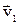і і 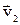. Після зіткнення утворюється частинка з масою 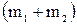, що випливає з умови адитивності маси в механіці. Швидкість 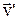частинки, що утворилася, можна знайти з закону збереження імпульсу: 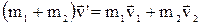. Зміну кінетичної енергії системи знайдемо із закону збереження енергії:

.

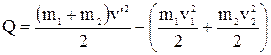Абсолютно пружним називають зіткнення, у результаті якого внутрішня енергія частинок не змінюється, а тому не змінюється і кінетична енергія системи. Нехай частинки масами m₁ і m₂ мають до зіткнення швидкост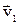і і 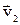. Після абсолютно пружного удару швидкості частинок будуть 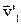і 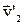відповідно. Закон збереження імпульсу і кінетичної енергії при цьому мають вигляд:

.

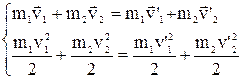Розв’язуючи отриману систему рівнянь, визначають швидкості частинок після зіткнення.

Date: 2015-07-01; view: 670; Нарушение авторских прав