
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Минимизация логических функций
|
|
Под минимизацией понимают приведение алгебраического выражения функции к более простому виду. В предыдущем параграфе мы это сделали на примере функции дизъюнкции двух переменных. Обобщая преобразования, можно сказать, что существуют стандартные приемы.
1. Прибавление одного или несколько однотипных членов из числа имеющихся в данной функции.
2. Умножение отдельных членов на сумму 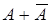 , где A может быть как одной из переменных, так и частью функции или даже самой функцией. При этом по аксиоме
, где A может быть как одной из переменных, так и частью функции или даже самой функцией. При этом по аксиоме 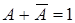 и аксиоме
и аксиоме 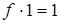 мы не меняем значения функции.
мы не меняем значения функции.
3. Выделение слагаемого типа 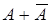 .
.
4. Использование законов склеивания: 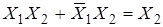 ,
, 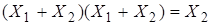 . Здесь пропадает переменная, имеющая свое отрицание.
. Здесь пропадает переменная, имеющая свое отрицание.
5. Применение правила де Моргана.
После всевозможных преобразований получается функция, не поддающаяся дальнейшему упрощению - тупиковая форма. Такая функция называется минимизированной. Она может быть представлена в дизъюнктивной форме (МДНФ) или конъюнктивной (МКНФ).
Алгебраический метод требует навыков в работе и интуиции.
Более просто проводить минимизацию с помощью карты Карно. Требование, что при переходе от терма к терму должна меняться только одна переменная, подсказывает, что теорема склеивания применяется к соседним минтермам (функция) или к соседним макстермам (Не функция). Имеется в виду соседство по строкам и столбцам. Диагональное соседство не учитывается. Если внимательно посмотреть на карту, то мы увидим, что соседними являются и крайние термы таблицы по конкретной строке или столбцу, то есть - карта Карно - развертка цилиндра по горизонтальной и вертикальной оси.
Правила склеивания:
1) сначала склеиваются восьмерки (если они есть);
2) затем склеиваются четверки (если они есть);
3) затем склеиваются двойки;
4) к полученным выражениям добавляются одиночные термы;
5) один и тот же терм может склеиваться сколько угодно раз (теорема тавтологии).
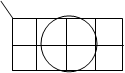
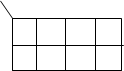
Примеры склеивания четверок:
 |  | ||||
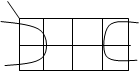 | |||||
 1 0 0 1 0 1 1 0 0 0 0 0
1 0 0 1 0 1 1 0 0 0 0 0
1 0 0 1 0 1 1 0 1 1 1 1
Другие примеры

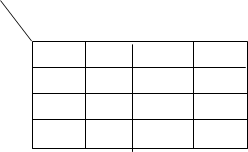
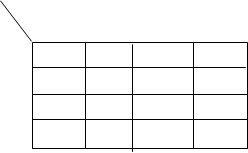
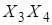 с
с

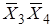
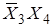
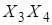
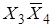



 а 1 0 0 1 а
а 1 0 0 1 а 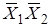 1а 1
1а 1

 0 1 1 0
0 1 1 0 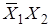 1 d
1 d
 0 1 b 1 0
0 1 b 1 0  1 b 1
1 b 1

 а 1 0 0 1 а
а 1 0 0 1 а 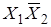 1 1
1 1
с
Два склеиваемых контура a и b, при склеивании четверок пропадают две меняющиеся переменные. Из рисунка с четырьмя контурами:
Контур a: 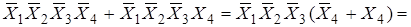
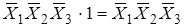 - пропала меняющаяся переменная X 4.
- пропала меняющаяся переменная X 4.
Контур b: меняются переменные X 2 и X 3. Следовательно, получим терм из неменяющихся переменных: 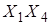 (проверьте).
(проверьте).
Контур c дает: 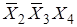
Контур d: 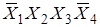 .
.
Итак, минимизированная функция будет
f = 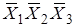 +
+ 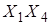 +
+ 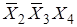 +
+ 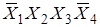 .
.
В случае, когда в карте Карно есть безразличные наборы Ф, вместо Ф ставят 0 или 1, исходя из удобства минимизации. Например:
   
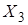 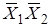 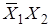  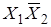
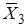 0 1 Ф 0 0 1 Ф 0
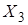 0 1 1 0 0 1 1 0
| Ясно, что выгоднее поставить 1, чтобы получить четверку, которая даст уменьшение количества переменных на 2. |
Date: 2015-07-01; view: 700; Нарушение авторских прав