Двойственность алгебры Буля

Увидеть двойственность можно просто, если проследить за алгоритмом вычисления простейших функций И и ИЛИ.

Рассмотрим функцию И. Здесь, если обе переменные равны 1, то функция X ₁ X ₂=1 истинна. Если же X ₁ и X ₂ равны нулю, то X ₁ X ₂ - ложна, но X ₁ + X ₂ - тоже ложна. Таким образом, для единиц мы имеем функцию И, а для нолей – ИЛИ (рис. 4.7).

Функция ИЛИ. Здесь, если X ₁=1 или X ₂=1 или X ₁ и X ₂ равны 1, то X ₁ + X ₂=1, т.е. функция истинна, но если X ₁=0 и X ₂=0, то справедливо и произведение X ₁ X ₂=0. Таким образом, для единиц мы имеет функцию ИЛИ, а для нолей – И (рис. 4.8).

Можно продемонстрировать двойственность и словами на таком примере:

1) в комнате ТЕПЛО, если батареи ВКЛЮЧЕНЫ И окно закрыто.

2) в комнате НЕ ТЕПЛО, если батареи НЕ ВКЛЮЧЕНЫ ИЛИ окно НЕ ЗАКРЫТО.

Двойственность: отрицаются аргументы и сама функция, а смысл остается одним и тем же. Возвращаясь к функциям И и ИЛИ, можно сказать, что если 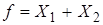, то двойственная к ней 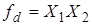получается заменой "+" на "*", и наоборот: , .

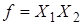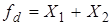Date: 2015-07-01; view: 488; Нарушение авторских прав