Элемент И-НЕ

Элемент И-НЕ реализует логическую функцию

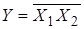
(отрицание конъюнкции).Эту операцию обозначают

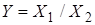
и называют функцией Шеффера или штрихом Шеффера. Условное обозначение элемента И-НЕ дано на рис. 4.12.

Элемент И-НЕ выполняет все основные логические операции:

а) операцию инверсии (рис. 4.13.1). При объединении ходов

.

б) операцию конъюнкции (рис. 4.13.2). Последовательное включение двух элементов, работающих как инверторы, между точкой подключения входного сигнала и соответствующим входом третьего элемента И-НЕ, позволяет реализовать функцию

,

т.е. операцию И;

в) операцию дизъюнкции (рис. 4.13.3). Включение двух элементов, работающих как инверторы, между точкой подключения входного сигнала и соответствующим входом третьего элемента И-НЕ, позволяет реализовать функцию

,

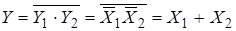т. е. функцию ИЛИ.

В общем случае как элементы ИЛИ-НЕ, так и элементы И-НЕ могут иметь не два, а n входов.

Для перехода в универсальный базис используют правило де Моргана. Покажем на примере "два из трех".

.

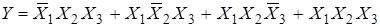1. В базисе И-НЕ.

Используем аксиому инверсии 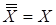и ставим над левой и правой частями двойное отрицание:

.

Раскрываем нижнее отрицание правой части по де Моргану:

.

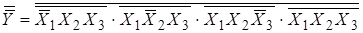2. В базисе ИЛИ-НЕ

.

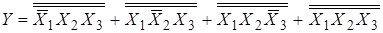Раскрываем нижние отрицания по де Моргану:

.

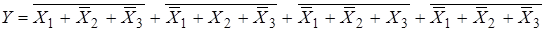Остается привести дизъюнкцию слагаемых к форме ИЛИ-НЕ

.

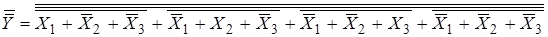Раскрывать общую инверсию здесь не следует.

Используя условные обозначения логических элементов, попытайтесь реализовать функцию Y в базисе И-НЕ или ИЛИ-НЕ. Не забывайте вводить для облегчения работы нумерацию термов и элементов.

Date: 2015-07-01; view: 408; Нарушение авторских прав