
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Карта Карно
|
|
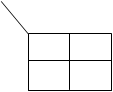
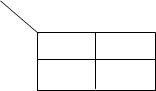
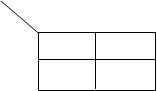
Карта Карно представляет собой таблицу всех возможных минтермов и макстермов функции. Пример построения карты для двух переменных:

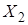
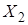



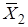
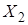

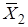
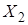
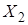
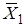

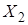
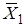
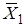
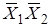
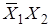
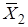
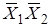
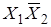 0 00 10
0 00 10


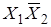

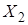
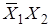
 1 01 11
1 01 11
По строке меняется переменная X 1, а по столбцу - X 2. В клетки заносятся произведения (термы) переменных в соответствии с пересечением строк и столбцов. Строки и столбцы можно менять местами. Вместо X можно ставить конкретные значения 0 или 1.
Карта Карно для трех и четырех переменных:




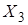
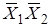
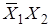

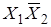
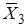
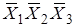
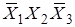
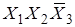
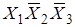
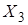
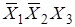
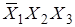
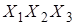
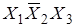
 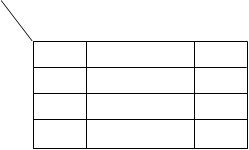 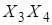
 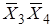 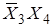 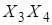 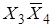
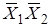 0000 0001 0011 0010 0000 0001 0011 0010
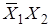 0100 0101 0111 0110 0100 0101 0111 0110
 1100 1101 1111 1110 1100 1101 1111 1110
 1000 1001 1011 1010 1000 1001 1011 1010
| Мы видим, что карта Карно перебирает все возможные наборы переменных. Обязательным условием карты Карно является то, что при переходе от клетки к клетке меняется только одна переменная. Например, изменения по верхней строке  . .
|
С помощью карты Карно можно задать функцию. Для этого сравнивают последовательно наборы таблиц состояний с термами карты. Если при каком-либо наборе значение функции равно 1, то в соответствующую этому набору клетку ставят 1.
   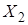 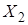
 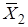 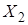  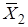 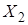
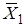 0 0 0 0 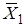 0 1 0 1
 0 1 0 1  1 1 1 1
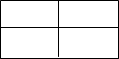
| Если набор дает нулевое значение функции, то ставят 0. Например, карта Карно для функций двух переменных |
Для построения алгебраического выражения функции, заданной картой Карно, следует просуммировать все термы, имеющие значение 1, и с помощью аксиом и теорем алгебры попытаться упростить полученное выражение. Например, для карты Карно функции И это всего лишь один терм  , т. е. f =
, т. е. f =  .
.
Для функции ИЛИ: 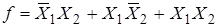 .
.
По аксиоме тавтологии добавим терм  :
:
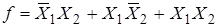 +
+  .
.
По закону ассоциативности (сочетательный):
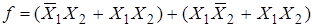 .
.
По закону дистрибутивности (распределительный):
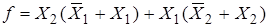 .
.
По аксиоме дополнительности 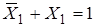 и
и 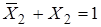 :
:
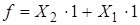 .
.
По аксиоме пересечения: 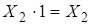 ,
, 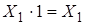 :
: 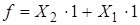 .
.
По закону коммутативности 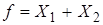 .
.
Из-за двойственности алгебры можно эту же функцию определить через макстермы, тем более что их всего один: 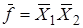 .
.
По де Моргану 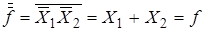 .
.
Иногда для некоторых наборов таблицы состояний значение функции может быть неизвестно. В этом случае значение функции может быть задано произвольно нулем или единицей по вашему усмотрению. Этот терм - безразличный набор, не влияющий на значение функции. Он необязателен. Договоримся обозначать его буквой Ф.
  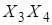
 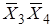 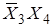 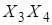 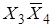
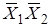 0 1 3 2 0 1 3 2
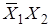 4 5 7 6 4 5 7 6
 12 13 15 14 12 13 15 14
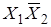 8 9 11 10 8 9 11 10
| Чтоб каждый раз не рисовать карту Карно, ввели нумерацию клеток. Обычно нумерация соответствует значению десятичных чисел в простом двоичном коде. При этом разряды двоичного числа растут справа налево 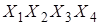 . При этом условии нумерация карты для четырех переменных такова. . При этом условии нумерация карты для четырех переменных такова.
|
Действительно, цифре 3 соответствует двоичное число 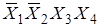 или 0001. Числу 15 -
или 0001. Числу 15 - 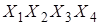 или 1111 и т. д.
или 1111 и т. д.
Функцию в дизъюнктивной форме (через единицы) задают в виде суммы номеров термов, имеющих единичное значение:
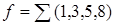 ,
,
то есть в клетках 1, 3, 5, 8 надо поставить 1, а в остальных нули.
Функцию в конъюнктивной форме задают (через нули) в виде произведения номеров термов, имеющих нулевое значение
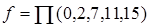 ,
,
то есть в клетках 0, 2, 7, 11, 15 надо проставить нули, а в остальных - единицы.
Безразличные наборы (Ф) приплюсовывают к S или P под названием ТНБ (термы, не доставляющие беспокойства).
 или
или 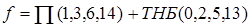 .
.
Date: 2015-07-01; view: 1215; Нарушение авторских прав