Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Логические функции
|
|
Существует несколько способов задания логических функций.
1. Словами. Например, для операции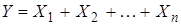 
значение функции истинно, если хотя бы один из ее аргументов принимает единичное значение.
2. Таблицей истинности. Например,
| X 1 | X 2 | X 3 | Y |
Функция Y соответствует так называемому мажоритарному элементу "2 из трех". Словами: "Функция истина, если по крайней мере два из трех аргументов равны 1". В таблице конкретный ряд (строка) значений аргументов, например, 0 1 0, называется набором. От табличной формы записи можно перейти к аналитической. Из таблицы видно, что значения функции истинны только для некоторых наборов значений переменных.
а) X 1 = 0, X 2 = 1, X 3 = 1, т. е. для сочетания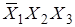 
;
б) X 1 = 1, X 2 = 0, X 3 = 1, т. е. для сочетания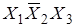 
;
в) X 1 = 1, X 2 = 1, X 3 = 0, т. е. для сочетания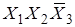 
;
г) X 1 = 1, X 2 = 1, X 3 = 1, т. е. для сочетания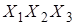 
.
Каждое из произведений переменных, для которых значение функции истинно, называется минтермом, или конституентом единицы, а функцию можно представить в виде суммы минтермов (т. к. каждый минтерм равен 1, то сумма равна 1):
Y = + + + .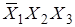
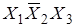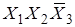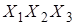Функция представлена в виде дизъюнкции произведений переменных или их отрицаний. Если каждое слагаемое содержит все переменные или их отрицания, то такая форма записи называется совершенной дизъюнктивной нормальной формой (СДНФ).
Совершенно также можно выделить и нулевые значения функции, имеющиеся в таблице: если истинное значение - это Y, то неистинное (нулевое) - это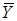 
:
а) X 1 = 0, X 2 = 0, X 3 = 0, т. е. для сочетания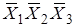 
;
б) X 1 = 0, X 2 = 0, X 3 = 1, т. е. для сочетания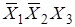 
;
в) X 1 = 0, X 2 = 1, X 3 = 0, т. е. для сочетания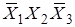 
;
г) X 1 = 1, X 2 = 0, X 3 = 0, т. е. для сочетания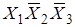 
.
Так как эти сочетания дают 0, то, сложив их, получим тоже 0:
= + + + .
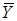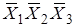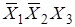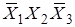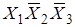Используя принцип двойственности или правило де Моргана, получим
.
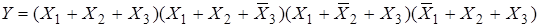Функция в этом случае задана в виде произведения (конъюнкции) сумм переменных или их отрицаний. Так как в суммы входят все переменные или их отрицания, то такая форма записи называется совершенной конъюнктивной нормальной формой (СКНФ).
Сами же суммы, для которых значение функции неистинно, называют макстермами, или конституентами нуля.
Date: 2015-07-01; view: 366; Нарушение авторских прав