
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Двухристальный нейтронный дифрактометр. Блок схема установки
|
|
Продвижение в область меньших углов рассеяния нейтронов позволяет осуществить двухкристальный дифрактометр на совершенных кристаллах. Схематически дифрактометр изображен на рис. 14.5.

| Рис. 14.5. Схема двухкристального дифрактометра на совершенных кристаллах. |
Первый кристалл служит монохроматором, а второй – анализатором пучка нейтронов, прошедших через прибор. Снятие информации осуществляется путем поворота кристалла-анализатора на угол в доли секунд (b) с последующей экспозицией в каждой точке, в это время кристалл-монохроматор должен быть неподвижен. По мере вращения кристалла-анализатора счёт на основном детекторе (интенсивность отражения) сначала возрастает, затем, проходя через максимум, уменьшается практически до фона. В случае одного отражения от кристалла образуется заметный “хвост”, спадающий как b –2. Способ подавления показан на рис. 14.5 – это использование в качестве монохроматора кристалла с пропилом, обеспечивающего многократное отражение пучка от одноимённых плоскостей (hkl). Для некоторых экспериментов также используется второй детектор, регистрирующий нейтроны, прошедшие через кристалл-анализатор.
В отсутствие образца интенсивность монохроматических нейтронов, отражённых от кристалла-анализатора, описывается формулой:
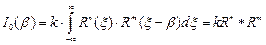 , ,
| (14.3) |
где k – постоянная величина, зависящая от характеристик нейтронного спектра и расходимости первичного пучка, 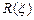 – коэффициент брэгговского отражения от “идеального” кристалла;
– коэффициент брэгговского отражения от “идеального” кристалла; 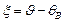 ;
; 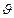 - угол падения луча, qB – угол Брэгга,
- угол падения луча, qB – угол Брэгга, 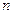 и
и 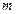 – число отражений нейтрона в монохроматоре и анализаторе соответственно. Очевидно схеме на рис. 14.5 отвечают
– число отражений нейтрона в монохроматоре и анализаторе соответственно. Очевидно схеме на рис. 14.5 отвечают 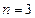 ,
, 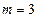 . Поясним происхождение формулы (14.3). Нейтрон, пройдя через систему коллиматоров, падает на монохроматор под углом
. Поясним происхождение формулы (14.3). Нейтрон, пройдя через систему коллиматоров, падает на монохроматор под углом 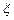 и отражается под тем же углом. Вероятность однократного отражения равна
и отражается под тем же углом. Вероятность однократного отражения равна 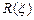 , соответственно n-кратного –
, соответственно n-кратного – 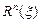 . После этого нейтрон падает на анализатор под углом
. После этого нейтрон падает на анализатор под углом 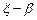 , отражается от него с вероятностью
, отражается от него с вероятностью  и попадает в детектор. Угол падения
и попадает в детектор. Угол падения 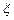 лежит в пределах от
лежит в пределах от  до
до 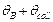 , где
, где  – разброс углов коллимации. Так как данный разброс много больше ширины линии отражения
– разброс углов коллимации. Так как данный разброс много больше ширины линии отражения 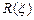 , то пределы интегрирования в (14.3) можно взять бесконечными. Кривая
, то пределы интегрирования в (14.3) можно взять бесконечными. Кривая 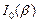 носит название инструментальной линии двухкристального дифрактометра.
носит название инструментальной линии двухкристального дифрактометра.
Коэффициент отражения от передней плоскости толстого совершенного кристалла определяется формулой Дарвина
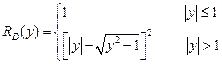 , ,
| (14.4) |
где 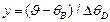 – нормированная разность угла падения и угла Брэгга. Параметр Дарвина
– нормированная разность угла падения и угла Брэгга. Параметр Дарвина 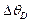 определяет полуширину кривой брэгговского отражения.
определяет полуширину кривой брэгговского отражения.
Получим выражение для экспериментально наблюдаемого распределения интенсивности малоуглового рассеяния нейтронов (МУРН). Пусть нейтрон падает на монохроматор под углом 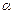 , тогда он отражается от него с вероятностью
, тогда он отражается от него с вероятностью 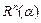 . Затем он рассеивается на образце на угол
. Затем он рассеивается на образце на угол 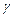 в горизонтальной плоскости с вероятностью
в горизонтальной плоскости с вероятностью  . Далее, если анализатор повернут на угол
. Далее, если анализатор повернут на угол 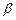 относительно монохроматора, то нейтрон падает на него под углом
относительно монохроматора, то нейтрон падает на него под углом 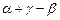 и отражается с вероятностью
и отражается с вероятностью 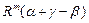 . Вероятность попадания нейтрона в детектор равна произведению указанных выше вероятностей, так как все отражения нейтрона независимы. Поскольку углы
. Вероятность попадания нейтрона в детектор равна произведению указанных выше вероятностей, так как все отражения нейтрона независимы. Поскольку углы 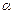 и
и 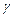 произвольны, по ним надо проинтегрировать. В итоге измеряемое угловое распределение интенсивности МУРН описывается следующим образом:
произвольны, по ним надо проинтегрировать. В итоге измеряемое угловое распределение интенсивности МУРН описывается следующим образом:
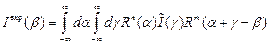 , ,
| (14.7) |
где, как и в (14.3) пределы интегрирования взяты бесконечными так как линии отражения от совершенных кристаллов много уже разброса углов в падающем пучке нейтронов. Легко видеть, что интеграл по 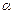 дает инструментальную линию, следовательно
дает инструментальную линию, следовательно
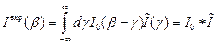 , ,
| (14.8) |
т.е. измеряемая интенсивность определяется сверткой инструментальной линии с линией рассеяния образца. Если 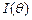 – вероятность рассеяния на угол
– вероятность рассеяния на угол 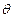 при прохождении через образец, то вероятность рассеяния на угол
при прохождении через образец, то вероятность рассеяния на угол 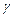 в горизонтальной плоскости получается интегрированием по углу рассеяния в вертикальной плоскости
в горизонтальной плоскости получается интегрированием по углу рассеяния в вертикальной плоскости
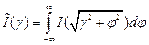 . .
|
Date: 2015-07-01; view: 603; Нарушение авторских прав