Рассеяние в борновском приближении. Псевдопотенциал Ферми

Запишем стационарное уравнение Шредингера (1.14) в виде

,

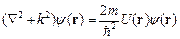(2.1)

где 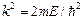. Из курса дифференциальных уравнений известно, что общее решение неоднородного дифференциального уравнения представляет собой сумму общего решения однородного дифференциального уравнения и частного решения неоднородного дифференциального уравнения. По аналогии с данной теоремой запишем решение (2.1) в виде

,

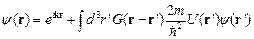(2.2)

где первое слагаемое − общее решение уравнения 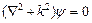, а функция Грина удовлетворяет уравнению

.

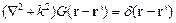(2.3)

Удостоверимся, что функция 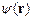из (2.2) является решением (2.1).

.

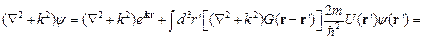
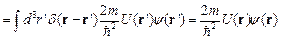Интегральное уравнение (2.2) называется уравнением Липпмана-Швингера, оно эквивалентно уравнению Шредингера (2.1). Однако при рассмотрении рассеяния интегральное представление имеет ряд преимуществ перед дифференциальным. В частности, уравнение (2.2) имеет вид: падающая плоская волна + рассеянная волна. Следовательно, из него непосредственно возникает связь между амплитудой рассеяния и потенциалом взаимодействия.

Решим уравнение (2.3) и найдем функцию Грина. Из (2.3) формально получаем

.

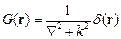Используя интегральное представление для 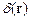, имеем:

.

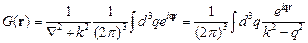(2.4)

Для вычисления интеграла перейдем к сферическим координатам (). Возьмем интеграл по направлению вектора .

.

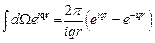(2.5)

Подставляя данное выражение в (2.4), получаем

.

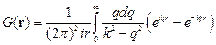(2.6)

Второе слагаемое в (2.6) можно преобразовать, использовав равенство

.

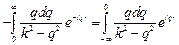Теперь во втором слагаемом подынтегральное выражение такое же, как в первом. Объединяя первое и второе слагаемые, имеем

.

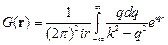(2.7)

Данный интеграл может быть вычислен с помощью теоремы о вычетах. Однако сначала надо выбрать правило обхода полюсов подынтегрального выражения, которые расположены на вещественной оси. Для этого предположим, что энергия имеет малую мнимую добавку, т.е. заменим 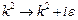, 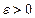и после вычисления вычетов возьмем предел 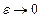. Так как 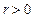, то подынтегральное выражение экспоненциально мало в верхней полуплоскости 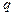. Поэтому можно замкнуть контур интегрирования в верхнюю полуплоскость как показано на рис. 2.1. Согласно теореме о вычетах интеграл (2.7) равен сумме вычетов внутри замкнутого контура, умноженной на 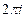. В данном случае есть один полюс в точке .

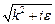Рис. 2.1. Контур интегрирования и полюса (к вычислению интеграла (2.7)).

В итоге в пределе 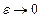получаем

.

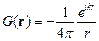Окончательно получаем решение уравнения (2.3)

.

(2.8)

При детектировании рассеянных нейтронов результат определяется значением функции 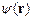на макроскопических расстояниях, много больших размера образца, т.е. . Возьмем приближенное значение пропагатора (2.8) с учетом данного условия, а именно: в знаменателе просто положим 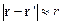, а в числителе учтем первый порядок разложения по малому параметру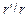

.

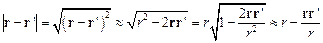Подставляя приближенное значение пропагатора в (2.2), получаем

.

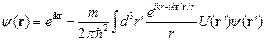(2.9)

Таким образом, волновая функция представляет собой сумму падающей плоской волны и рассеянной сферической

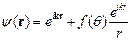	,	(2.10)
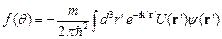	,	(2.11)

где 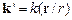− волновой вектор волны, рассеянной в направлении , 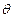− угол между 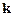и 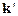, т.е. угол рассеяния.

Мы перешли от уравнения Шредингера к соотношениям (2.10), (2.11) с использованием только условия . Однако, если рассеивающий потенциал мал, то из (2.11) сразу получаем выражение для амплитуды рассеяния. В самом деле, если мал, то рассеянная волна много меньше падающей. Соответственно в (2.11) можно положить 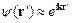. При этом мы считаем, что рассеивается на ядрах только падающая плоская волна, и пренебрегаем тем, что рассеянная волна (нейтрон) может рассеяться вторично. В итоге получаем выражение для амплитуды рассеяния в борновском приближении

,

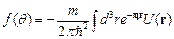(2.12)

где мы ввели вектор рассеяния с абсолютной величиной

.

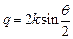Видно, что в борновском приближении формула для амплитуды рассеяния довольно проста: амплитуда пропорциональна Фурье-образу потенциала рассеяния.

Борновское приближение часто используется при описании рассеяния нейтронов в конденсированных средах. Однако при рассеянии медленных нейтронов на ядрах заме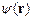на на недопустима. Ядерное взаимодействие является сильным и значительно искажает волновую функцию в пределах своего радиуса действия. С другой стороны, вычислить почти для всех ядер не удается, и найти амплитуду ядерного рассеяния из первых принципов не представляется возможным. Но если использовать амплитуду ядерного рассеяния 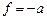как уже известную величину, то в дальнейшем можно ввести фиктивный потенциал (псевдопотенциал Ферми). Обычно его записывают в виде

.

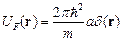(2.16)

Потенциал 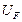не является истинным взаимодействием между ядром и нейтроном. Полагая, однако, что он является таким взаимодействием, а также принимая, что это взаимодействие слабое, получаем в борновском приближении (2.12)

,

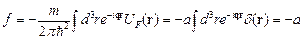(2.17)

что совпадает с определением длины рассеяния. Другими словами, неверный потенциал 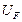после подстановки в выражение для неверного (борновского) приближения дает правильный результат. Это делает потенциал Ферми (2.16) очень удобным при описании реального рассеяния тепловых нейтронов ядрами, закрепленными и движущимися в конденсированных средах с тепловыми скоростями.

Date: 2015-07-01; view: 841; Нарушение авторских прав