Брэгговское рассеяние на ядрах без спина. Изотопическая некогерентность

Пусть имеется группа ядер, находящихся в точках с координатами 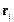. Из соотношения (3.3) следует, что рассеяние на большом числе ядер описывается волновой функцией

,

(5.1)

где 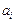– длина рассеяния i- го ядра. Координаты 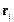лежат внутри образца, размер которого всегда много меньше расстояния до детектора. Так как наблюдаемые величины зависят от волновой функции 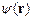на месте детектора, то в (5.1) надо положить 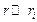. При этом

,

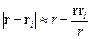(5.2)

и с учетом того, что 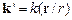, (5.1) принимает вид

,

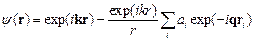(5.3)

где 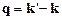– изменение импульса нейтрона при рассеянии. Коэффициент при сферической волне равен амплитуде рассеяния. Значит, для длины рассеяния на ансамбле ядер имеем

.

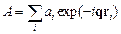(5.4)

Между рассеяниями единичным ядром и ансамблем ядер существует большое различие: если первое изотропно, то второе очевидно не изотропно. Заметим, что из данного результата следует, что взаимодействие нейтрона с ансамблем ядер характеризуется псевдопотенциалом Ферми

.

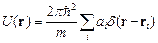(5.5)

Действительно, подставляя эту энергию в формулу Борна (2.12), получаем для длины рассеяния на выражение (5.4). Дифференциальное сечение рассеяния, следующее из (5.4), имеет вид

.

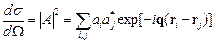(5.6)

Предположим сначала для простоты, что мишень состоит из ядер одного сорта, спин которых равен нулю. Тогда все коэффициенты 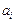имеют одну и ту же величину а, а выражение (5.6) можно переписать в виде

.

(5.7)

Предположим далее, что мишень представляет собою кристалл с одним атомом в элементарной ячейке. Тогда двойная сумма в (5.7) сводится к 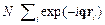, где N – число рассеивающих ядер, а сумма берется по всем ячейкам. Хорошо известно, что эта сумма обращается в нуль, если вектор 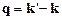не является вектором обратной решетки 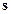. Можно показать, что

,

(5.8)

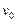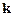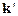где — объем элементарной ячейки. Мы видим, что рассеяние сильно анизотропно и имеет место лишь для определенных ориентации волновых векторов падающих и рассеянных нейтронов и при 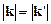, таких, что 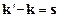. Различные пики рассеяния в направлении 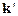, возникающие при соответствующей ориентации вектора 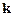по отношению к кристаллу, называют брэгговскими пиками. Другого рассеяния, помимо брэгговского, не существует. Можно сказать, что рассеяние полностью когерентно. Условия 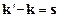, 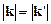требуют, чтобы векторы 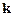и 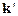составляли с плоскостью решетки, перпендикулярной вектору 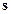, один и тот же угол 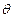и выполнялось равенство или 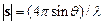. Отсюда следует, что, если 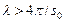, где — наименьший вектор обратной решетки, брэгговское рассеяние не имеет места. Длина волны 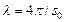называется длиной волны обрезания.

По определению вектора обратной решетки 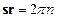, где 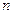– целое число. Соответственно вся кристаллическая решетка разбивается на систему параллельных плоскостей, ортогональных вектору 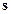. Расстояние между 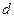соседними плоскостями равно 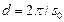. Наличие -функций в (5.8) приводит к условию 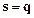, из которого, выбирая векторы обратной решетки в виде 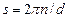, получаем, что . Выражая волновой вектор через длину волны из (5.8) получаем известное условие Брэгга

.

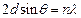(5.9)