Многократное малоугловое рассеяние нейтронов. Формула Мольер

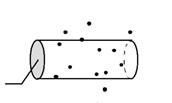
Одной из характеристик движения нейтрона в среде является величина, называемая длиной свободного пробега нейтрона 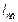. Это среднее расстояние, которое нейтрон проходит в материале без рассеяния, или, другими словами, на этой длине рассеивается в среднем один раз. Найдем связь длины рассеяния с параметрами образца. Пусть образец имеет вид, как показано на рис.7.3а, т.е. это толстый (толщины L) образец со случайным расположением в нем неоднородностей. Нейтрон, влетая в вещество, взаимодействует с неоднородностями, размеры которых существенно превышают характерные размеры нейтрона. Поскольку нам важны сами факты рассеяния, представим себе картину движения нейтрона в среде иначе (см. рис.7.3б). Пусть теперь нейтрон имеет размер, равный среднему размеру неоднородностей, а сами рассеивающие центры имеют точечные размеры. Очевидно, что вероятность рассеяния от этого не изменится. Теперь нейтрон, двигаясь в среде, заметает некоторый объем и число актов рассеяния равно числу точек (расеивателей) в этом объеме. Таким образом одного нейтрона получаем цилиндр взаимодействия некоторой длины l и площадью основания, равной полному сечению рассеяния .

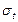а б

Рис. 7.3. К выводу формулы для длины рассеяния.

Пусть N – количество рассеивателей, которые попали в этот цилиндр. Тогда

,

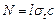(7.9)

где с – концентрация неоднородностей. Полагая в формуле (7.9) получаем, что

.

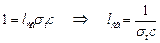(7.10)

Если толщина образца 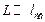, то рассеяние является однократным. При этом можно пренебречь тем, что нейтрон, рассеянный на одной неоднородности, может еще раз рассеяться на другой неоднородности. В обратном случае 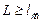рассеяние называется многократным. Для описания такого рассеяния обычно используется теория Мольер, предполагающая, что неоднородности в образце расположены абсолютно случайно, и, следовательно, рассеянные волны от различных неоднородностей складываются некогерентно.

Вместо вектора рассеяния удобно рассматривать безразмерный вектор 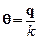. Так как модуль этого вектора равен углу рассеяния 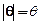, мы будем также называть его углом рассеяния.

Рассмотрим сначала однократное рассеяние. Вероятность однократного рассеяния нейтрона на угол 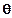равна

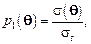где 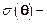дифференциальное сечение рассеяния нейтрона на угол .

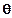Вероятность получить полный угол рассеяния 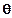при взаимодействии с двумя рассеивающими центрами имеет вид:

.

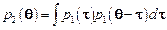(7.11)

Действительно, если нейтрон первый раз рассеялся на угол 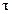, то во второй раз ему необходимо рассеяться на угол 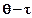, чтобы суммарный угол рассеяния был равен 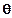. Считая данные события независимыми, перемножаем их вероятности. Так как угол 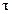может быть любым, то в (7.11) интегрируем по 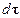. Поскольку подынтегральное выражение отлично от нуля только при малых 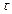, то пределы интегрирования можно взять бесконечными. Аналогично получаем вероятность n-кратного рассеяния на угол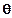

.

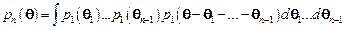(7.12)

Пусть фурье-образ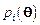

.

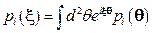Переход в Фурье-пространство значительно упрощает задачу, поскольку свертка функций в выражении (7.12) превращается в их произведение

.

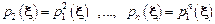(7.13)

В образце нейтрон может рассеяться произвольное количество раз. Интенсивность рассеяния на угол 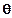на образце толщиной L будет выражаться суммой по всем кратностям рассеяния

,

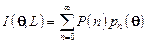(7.13)

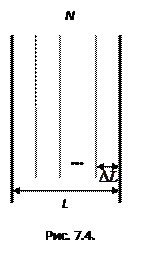где 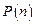– вероятность того, что нейтрон рассеется n раз. Здесь значению 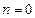отвечают нейтроны, прошедшие образец, не испытав рассеяния. Очевидны следующие соотношения: 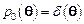, 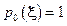. Фурье представление интенсивности рассеяния

.

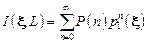(7.14)

Найдем вероятности P (n). Для этого разобьем образец на слоев (см. рис. 7.4) толщиной 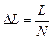. Вероятность рассеяться в одном тонком слое равна

.

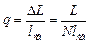(7.15)

Вероятность, что нейтрон в 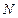слоях рассеется 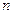раз, определяется биномиальным распределением

.

Для получения окончательного выражения надо устремить число слоев к бесконечности. Так как при 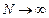произведение 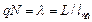остается постоянным, то биномиальное распределение переходит в распределение Пуассона

.

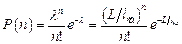(7.16)

Подставляя (7.16) в (7.14), получаем

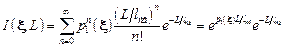
Учитывая, что 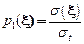находим фурье-образ интенсивности рассеяния

.

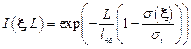(7.17)

Совершая обратное преобразование Фурье, получаем:

.

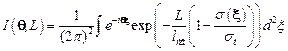(7.18)

Эта формула называется формулой Мольер, она широко используется при изучении материалов методом многократного малоуглового рассеяния нейтронов.