Оптическая свойство эллипса

Утверждение. Касательная к эллипсу образует одинаковые углы с локальными радиусами.

Доказательство. Пусть - касательная к эллипсу в точке с уравнением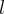

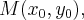
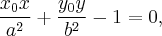
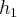- расстояние до касательной от левого 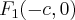фокуса и 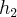- расстояние от правого 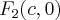фокуса. Тогда

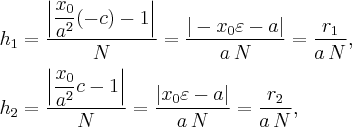
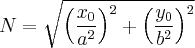
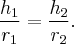
где - модуль вектора нормали касательной. Итак,

Последнее равенство означает равенство синусов углов, образованных локальными радиусами с касательной. Но так как оба угла острые, то из равенства синусов следует равенство самых углов.

Если представить эллипс как зеркальную кривую, то по законам оптики луч света, выпущенный с одной фокуса, после отражения от эллипса пройдет через второй фокус.

Источник: Файл:Ellipse with focus.svg - https://ru.wikipedia.org

Источник: Файл:ElipseAnimada.gif - https://ru.wikipedia.org

шҐ˜ю~ э

Источник: Файл:Parametric ellipse.gif - https://ru.wikipedia.org

Гипербола.

ГМТ, координаты которых относительно некоторой прямоугольной декартовой системы координат удовлетворяют уравнению

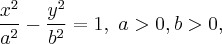
называется гиперболой. Данное уравнение называется каноническим уравнением гиперболы, а соответствующая система координат называется канонической. Есл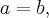и то гипербола называется равносторонний.

Следующие два утверждения дают представление о форме гиперболы.

Первое. Любая гипербола выходит из равносторонней путем сжатия (растяжения) плоскости вдоль оси 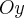с коэффициентом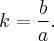

Действительно, пусть точка 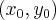принадлежит равностороннего гиперболе, то есть 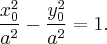Легко проверить, что в таком случае точка с координатами 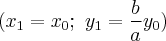принадлежит гиперболам

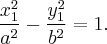
Второе. равностороннего гипербола 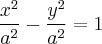получается поворотом на угол 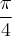графика обратной пропорциональной зависимости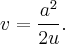

Пусть 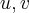декартовы координаты, и 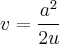график обратной пропорциональной зависимости. Осуществим вращения плоскости на угол 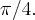Аналитическое задание такого преобразования

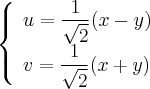
Итак, в новых координатах получаем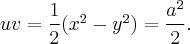

Геометрическими характеристиками гиперболы являются:

· две оси симметри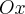и и 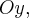один центр симметрии - точка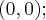

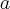
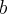
· параметр - действительно полуось, параметр - мнимая полуось;

· величина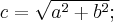

· точки 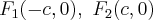называются левым и правым фокусами (очаговыми точками) } соответственно;

· величина - фокусное расстояние, то есть расстояние между фокусами;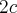

· величина 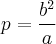– фокальный параметр;

· величина – эксцентриситет;

· точки - вершины гиперболы (пересечение гиперболы с осью симметрии);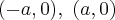

· две прямые - директрисы гиперболы;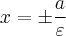

· две прямые - асимптоты гиперболы.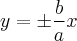

Date: 2015-07-01; view: 1830; Нарушение авторских прав