Относился к притче

Утверждение. Если точка 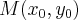принадлежит параболе, то уравнение касательной к параболе в этой точке имеет вид:

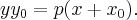
Доказательство. Действительно, рассмотрим точки параболы в полуплоскости 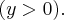Тогда 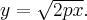Поскольку уравнение касательной для явно заданной кривой имеет вид 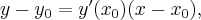а 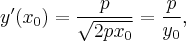то имеем

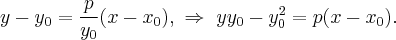
Поскольку 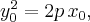получаем 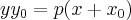- уравнение касательной.

Пример. Написать уравнение касательной к параболе 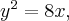параллельной прямой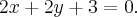

Решать эту задачу можно двумя способами.

1 способ. Записываем уравнение касательной к параболе в неизвестной точке 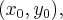принадлежащей параболе:

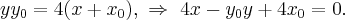
Эта касательная должна быть параллельна прямой 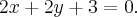Условие параллельности двух прямых:

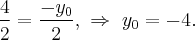
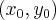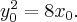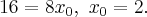Поскольку точка принадлежит параболе, то Итак, Уравнение искомой касательно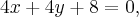й или

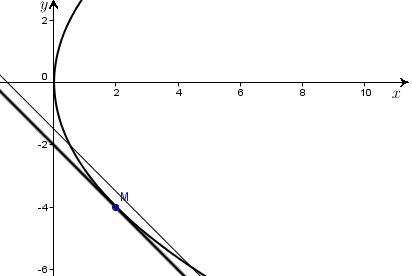
2 способ. Записываем уравнение прямой, параллельной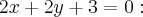

Ищем точки пересечения прямой и параболы

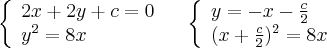
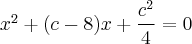
Касательная имеет с кривой единую двойной точку пересечения, то есть дискриминант должен равняться нулю. Итак 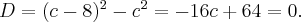Отсюда 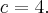Точку соприкосновения ищем при

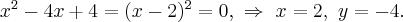
Итак уравнение касательной или

Date: 2015-07-01; view: 751; Нарушение авторских прав