
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формульный инструметарий
|
|
| Общий расчет производится по традиционной технологии дисконтирования и сопоставления денежных поступлений и оттоков капитала предприятия по данному объекту: |
| Показатель, объяснение | Формулы, методики для расчетов | Обозначение |
| 1. Будущая стоимость денежной единицы (сложный процент) | (1) FV = РV{1 + r)n | FV - будущая стоимость; РV - первоначальный взнос (текущая стоимость); r - процентная ставка (ставка дисконта); n - число периодов начисления процентов; (1 + r) n - фактор будущей стоимости; (фактор накопления); |
| При более коротком периоде начисления процента ставку следует откорректировать, например, если предполагается начисление процентов ежемесячно то базовая формула -1.1, а если поквартально, то формула принимает вид 1.2 | (1.1) FV=PV(1+r/12)n*12 (1.2) FV=PV(1+r/4)n*4 | FV - будущая стоимость; РV - первоначальный взнос (текущая стоимость); r - процентная ставка (ставка дисконта); n - число периодов начисления процентов; |
| 2. Текущая стоимость единицы (дисконтирова-ния) | (2) PV=FV/(1+r)n | FV - будущая стоимость; РV - первоначальный взнос (текущая стоимость); r - процентная ставка (ставка дисконта); n - число периодов начисления процентов; 1 / (1 + r) n - дисконтный множитель (фактор текущей стоимости); |
| 3. Обычный аннуитет (определяется как сумма равновеликих платежей, осуществляемых в конце периода) | (3)PVA=A*(1-(1+r)-n ) /r | PVA - текущая стоимость аннуитета; А - платеж п-го периода; 1 - (1 + r)-n / r - фактор текущей стоимости аннуитета, дисконтный множитель аннуитета; |
| 4. Авансовый аннуитет (имеет место в условиях временного совпадения первого платежа с депонированием основной суммы вклада). | (4)PVA=A*(((1-(1+r)-(n-1))/r) +1) | PVA - текущая стоимость аннуитета; А - платеж п-го периода; |
| 5. Периодический взнос на погашение ссуды (взнос на амортизацию единицы). | (5) А=PVA:((1-(1+r)-(n-1))/r) | 1: ((1 - (1 + r) - (n-1)) / r) - фактор взноса на амортизацию, фактор взноса в погашение ссуды; PVA - текущая стоимость аннуитета; А - платеж n-го периода; |
| 6. Будущая стоимость обычного аннуитета. | (6)FVA=A*(((1+r)n-1)/r) | FVA - будущая стоимость аннуитета; ((1 + r) n-1) / r - фактор будущей стоимости аннуитета; A - платеж n-го периода; |
| 7 Будущая стоимость авансового аннуитета. | (7) FVA= A*(((1+r)n-1)/r)*(1+r) | FVA - будущая стоимость аннуитета; ((1 + r) n-1) / r - фактор будущей стоимости аннуитета; A - платеж n-го периода; |
| 8. Периодический взнос в фонд накопления | (8) А =FVA*r/(1+r)n-1 | r / (1 + r) n-1 - фактор периодического взноса в фонд накопления, фактор взноса в фонд возмещения; FVA - будущая стоимость аннуитета; A - платеж n-го периода; |
Методы расчета ставки дисконта
| 9.1.Метод кумулятивного построения |
(9.1) r=rбаз+ 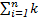
| rбаз-базовая безрисковая ставка дисконта; ki - компенсация за i-ый риск; п - количество учтенных рисков; | |
| 9.2. Метод сопоставимой продажи | (9.2) r = 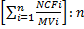
| 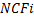 - чистый операционный поток капитала за и-тем объектом; - чистый операционный поток капитала за и-тем объектом;
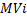 , - рыночная стоимость i-того объекта-аналога;
п - количество рыночных аналогов, доступных на рынке; , - рыночная стоимость i-того объекта-аналога;
п - количество рыночных аналогов, доступных на рынке;
| |
| 9.3. Метод капитальных активов | (9.3) r =rбаз+ 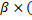 pрин – rбаз) pрин – rбаз)
| rбаз - базовая безрисковая ставка дисконта; β - коэффициент системного риска; ррин - средняя доходность рынка; | |
| 9.4.1. Метод сопряженных инвестиций: для собственного и заемного капитала; | (9.4.1) r =q+рк+(1-q)  рa рa
| q - доля заемных источников финансирования в общей сумме капитала предприятия; рк - средняя доходность заемного капитала; ра - нормальная доходность собственного капитала; | |
| 9.4.2. Метод сопряженных инвестиций: для составных элементов объекта | (9.4.2) r = qзем  rзем+qнер rзем+qнер  rнер+...+qn+rn rнер+...+qn+rn
| qзем - доля стоимости земли в общей стоимости объекта rзем - ставка дисконта для земли; qнер - доля стоимости недвижимости в общей стоимости объекта; rнер - ставка дисконта для недвижимости; qn - доля стоимости п-го элемента в общей стоимости объекта; rn - ставка дисконта для п-го элемента; |
| 9.5 Метод средневзвешенной стоимости капитала | (9.5) r=qп  vп+qв vп+qв  vв+...
+qN vв+...
+qN  vN vN
| qп - доля кредита в общем объеме финансирования объекта; vп - кредитная ставка; qв - доля собственного капитала в общем объеме финансирования объекта; vв - стоимость использования собственного капитала; qN - доля п-го источника финансовых ресурсов в общем объеме финансирования объекта; vN - стоимость использования п-го источника финансирования; |
| 9.6 Метод внутренней нормы доходности | (9.6) 0= 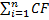 + i + i  Fmi( Fmi( 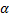 ) –
- ) –
- 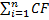 - i - i  Fmi( Fmi( 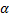 ) )
| 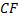 + - притоки капитала предприятия за i-тый год (период); + - притоки капитала предприятия за i-тый год (период);
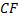 - - оттоки капитала предприятия за i-тый год (период);
п - количество прогнозных периодов оценки;
Fmi( - - оттоки капитала предприятия за i-тый год (период);
п - количество прогнозных периодов оценки;
Fmi(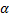 ) - дисконтный множитель, определенный как соответствующая функция денежной единицы для i-го периода по предварительно устанавливается-ной ставке а по отношению к базовому периоду. Отсюда выводится значение учетной ставки, хотя это и связано с трудностями математического характера; ) - дисконтный множитель, определенный как соответствующая функция денежной единицы для i-го периода по предварительно устанавливается-ной ставке а по отношению к базовому периоду. Отсюда выводится значение учетной ставки, хотя это и связано с трудностями математического характера;
|
| 9.7. Метод ставки LIBOR | (9.7) r = LIBOR + 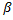 к (1...2%) к (1...2%)
| LIBOR - стоимость продажи денег на европейских валютных рынках;
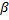 к – уровень риска в стране; к – уровень риска в стране;
|
| 10. Чистый приведенный поток капитала | (10) NCF= 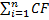 + i + i  Fmi–
- Fmi–
- 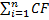 - i - i  Fmi Fmi
| NCF - чистый приведенный поток капитала;
СF+ - притоки капитала предприятия за i-тый год (период);
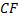 - - оттоки капитала предприятия за i-тый год (период);
п - количество прогнозных периодов оценки;
Fmi - дисконтный множитель, определенный как соответствующая функция денежной единицы для i-го периода по предварительно устанавливается-ной ставке а по отношению к базовому периоду. Отсюда выводится значение учетной ставки, хотя это и связано с трудностями математического характера; - - оттоки капитала предприятия за i-тый год (период);
п - количество прогнозных периодов оценки;
Fmi - дисконтный множитель, определенный как соответствующая функция денежной единицы для i-го периода по предварительно устанавливается-ной ставке а по отношению к базовому периоду. Отсюда выводится значение учетной ставки, хотя это и связано с трудностями математического характера;
|
| 11. Ставка капитализации | (11) kкап=к-t | kкап - ставка капитализации; r - ставка дисконта; t - ожидаемые среднегодовые темпы; роста прибыли или денежного потока |
Задачи
Пример 1. Заем 250 ООО грн. амортизируется в течение 5 лет путем годовых выплат в конце года так, что каждая последующая выплата долга больше предыдущей на 5%. Годовая ставка процента 12%. Составьте план амортизации
Решение
Учитывая математический инструментарий, применяемый в экономике имеем возможность использовать формулу геометрической прогрессии, аналог сложных процентов:
U1 = S (q-1) / (qn - 1) = 250000 * (1,05-1) / (1,055 - 1) = 45243,7 грн.
3 формулы геометрической прогрессии:
U1= 45 243,7 х 1,05 = 47 505,88;
U2 = 47 505,88 х 1,05 = 49 881,18...
График погашения амортизации долга в этом случае имеет вид табл. 5.10.
| № взноса | Общий взноса (ст. 5 + ст. 4) | назначение взноса | Баланс | |
| прибыль заимодавца | Доля вклада на погашение займа | |||
| 250 000 | ||||
| 75 243,7 | 30 000 | 45 243,7 | 204 756,3 | |
| 72 076,64 | 24 570,76 | 47 504,88 | 157 250,42 | |
| 68 751,23 | 18 870,05 | 49 881,18 | 107 369,24 | |
| 65 259,55 | 12 884,31 | 52 375,24 | 54 994,0 | |
| 61 593,28 | 6 599,28 | 54 994,0 | ||
| Всего | 342 924,4 | 92 924,4 | 250 000 |
Date: 2015-07-17; view: 444; Нарушение авторских прав