
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Требования к уровню подготовки учащихся 6 page
|
|
Для решения задачи воспользуемся алгоритмом получения СДНФ по таблице истинности
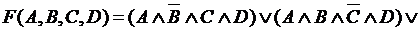
 .
.
в) Получили логическую функцию F(A,B,C,D), функцию от четырёх переменных, минимизируем её Минимизация булевой функции – это преобразование функции к такому виду, когда она содержит наименьшее возможное число логических переменных и наименьшее возможное число операций над ними. Применим два способа минимизации исследуемой функции.
1-й способ. Для минимизации функции воспользуемся основными законами логики. По закону идемпотентности дизъюнкции можно записать
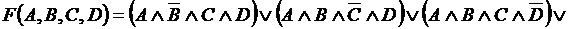
 .
.
Попарно сгруппируем выражения в скобках и применим закон дистрибутивности конъюнкции относительно дизъюнкции
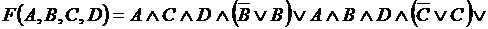
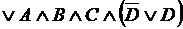 .
.
По закону исключённого третьего имеем
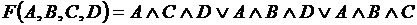 .
.
Далее, применив закон дистрибутивности конъюнкции относительно дизъюнкции, получим структурную формулу [5] для функции F – информационную модель:
 .
.
2-й способ. Воспользуемся картами Карно (диаграммами Вейча) для четырёх переменных[6] (рис. 37).
| C D A B |  01 01
| |||
Рис. 37
C использованием карт Карно получим структурную формулу для функции F такого вида:
 .
.
г)
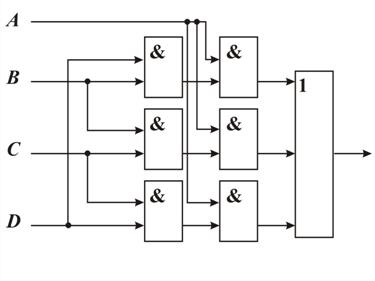
|
| Рис. 38 |
По полученному выражению, задающему логическую функцию F, составим функциональную схему[7] необходимого устройства, информационную модель процесса голосования (рис. 38).
д) Составим по функциональной схеме компьютерную модель процесса голосования, например с использованием программы «Конструктор логических схем» (для проведения компьютерного эксперимента).
Схема перехода от практической задачи к компьютерной модели




 Реальный объект Системный анализ Табличная информационная модель Структурная формула (информационная модель) Функциональная схема (информационная модель) Компьютерная модель (программа или электронная схема, сконструированная на специальном программном обеспечении, реализующая процесс голосования с помощью выбранного исполнителя).
Реальный объект Системный анализ Табличная информационная модель Структурная формула (информационная модель) Функциональная схема (информационная модель) Компьютерная модель (программа или электронная схема, сконструированная на специальном программном обеспечении, реализующая процесс голосования с помощью выбранного исполнителя).
Задача о расписании
Может ли компьютер оказать помощь человеку в составлении расписания, например, расписания движения поездов, автобусов, расписания всевозможных дежурств, уроков? Это очень трудоёмкий процесс, при составлении расписания необходимо учитывать многие факторы. Проведём эксперимент, попробуем составить расписание уроков с использованием компьютера на один день в восьмом классе общеобразовательной школы.
Задача 2. Составьте расписание уроков на один день занятий, учитывая следующие предварительные пожелания учителей
· В планируемый день занятий у учащихся должно быть 4 урока.
· Учитель информатики может провести либо 1-й, либо 2-й, либо 3-й уроки.
· Учитель литературы может провести либо 2-й, либо 3-й уроки.
· Учитель математики может провести либо 1-й, либо 2-й уроки.
· Учитель физкультуры согласен проводить только последний урок.
Решение. Решим задачу алгебраическим методом. Алгебраический метод решения логических задач является универсальным. Можно рекомендовать такой алгоритм решения логических задач алгебраическим методом.
· Проанализируй условие задачи.
· Введи систему обозначений для логических высказываний.
· Сконструируй логическую функцию, описывающую логические связи между всеми заданными высказываниями задачи – составь информационную модель.
· Упрости выражение, задающее сконструированную функцию.
· Определи значения истинности этой логической функции, для этого составь компьютерную модель, рассчитанную на выбранного исполнителя.
· Из полученных значений истинности функции определи значения истинности введенных логических переменных. По значению переменных сделай заключение о решении задачи.
A. Реализуем первый и второй этапы решения логических задач. Введём следующие обозначения. I1 (I2, I3) – учитель информатики проводит свой урок первым (вторым, третьим) уроком. L2 (L3) – учитель литературы проводит свой урок вторым (третьим) уроком. M1 (M2) – учитель математики проводит свой урок первым (вторым) уроком. F4 – учитель физкультуры проводит свой урок четвёртым уроком. Выбрали восемь логических переменных, с их помощью формализуем решение задачи.
B. Составим информационную модель в виде логической функции, описывающей взаимосвязь между исходными простыми высказываниями. Значение формируемого выражения присвоим переменной DAY. Найдём совокупность значений (I1, I2, …, F4), которые обратят уравнение Day = true в верное равенство. В день у учеников должно быть 4 разных урока. Условие того, что урок информатики проведён, запишется в виде некоторого логического выражения, его значение присвоим переменной INF. Для других предметов будем соответственно использовать переменные LT, MT, FZ. О правильности расписания будут говорить истинные значения этих переменных. Кроме того, в правильно составленном расписании не должно быть наложений. Например, не могут быть одновременно первым уроком информатика и математика. Обозначим высказывание об отсутствии наложений в расписании на первом уроке – Less1, соответственно высказывание об отсутствии наложений в расписании на втором уроке – Less2, на третьем – Less3. Для четвёртого урока такое условие можно не записывать, так как на это время никто не претендует, кроме учителя физкультуры.
DAY=INF и LT и MT и Less1 и Less2 и Less3.
Выведем зависимость каждого отдельного условия от исходных данных. Начнём с урока информатики. Записать пожелания учителя информатики можно логическим выражением INF= I1 or I2 or I3. Высказывание INF должно принимать истинное значение для того, чтобы учитель информатики был доволен расписанием. Аналогично рассуждая, запишем высказывания для других предметов. Пожелания учителя литературы запишем высказыванием LT = L2 or L3. Пожелания учителя математики запишем высказыванием MT=M1 or M2.
Определим высказывания Less1, Less2, Less3, Less4. Less1 = (I1 and not M1) or (not I1 and M1), Less2 = (I2 and not M2 and not L2) or (not I2 and M2 and not L2) or (not I2 and not M2 and L2), Less3 = (I3 and not L3) or (not I3 and L3). Полученные значения логических переменных поставим в функцию Day, логическую функцию от семи переменных. DAY=INF and LT and MT and Less1 and Less2 and Less3. В силу того что на четвертый урок нет претендентов, кроме учителя физкультуры, то четвертый урок можно исключить из рассмотрения.
C. Определим, для какой совокупности значений семи логических переменных I1, I2, I3, L2, L3, M1,M2 функция Day принимает значение true. То есть составим таблицу истинности для полученной функции и выберем из неё строки, где значение Day истинно. Для решения поставленной задачи воспользуемся компьютером. Составим компьютерную модель процесса составления таблицы истинности функции Day и выбора совокупности значений логических переменных, при которых значение функции истинно.
Компьютерная модель решаемой задачи
procedure TForm1.Button1Click(Sender: TObject);
var I1, I2, I3, L2, L3, M1, M2, Day, Less1, Less2, Less3, INF, LT, MT: Boolean; i:byte;
begin
with stringgrid1 do
begin
cells[1,0]:='Инф.1';cells[2,0]:='Инф.2';cells[3,0]:='Инф.3';
cells[4,0]:='Литер.2';cells[5,0]:='Литер.3'; cells[6,0]:='Матем.1';
cells[7,0]:='Матем.2';
end;
i:=1;
for I1:=False to True do for I2:=False to True do for I3:=False to True do
for L2:=False to True do for L3:=False to True do for M1:=False to True do
for M2:=False to True do
begin
INF:= I1 or I2 or I3; LT:= L2 or L3; MT:=M1 or M2;
Less1:=(I1 and not M1) or (not I1 and M1);
Less2:=(I2 and not M2 and not L2) or (not I2 and M2 and not L2);
Less2:=Less2 or (not I2 and not M2 and L2);
Less3:=(I3 and not L3) or (not I3 and L3);
DAY:=INF and LT and MT and Less1 and Less2 and Less3;
if DAY then
begin
//добавить новую строку в таблице для вывода результата
StringGrid1.RowCount:=StringGrid1.RowCount+1;
with Stringgrid1 do
begin
cells[1,i]:=BooltoStr(I1,true);cells[2,i]:=BooltoStr(I2,true);
cells[3,i]:=BooltoStr(I3,true);cells[4,i]:=BooltoStr(L2,true);
cells[5,i]:=BooltoStr(L3,true);cells[6,i]:=BooltoStr(M1,true);
cells[7,i]:=BooltoStr(M2,true);
end; i:=i+1; end; end; end;
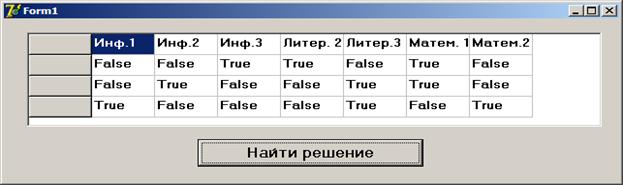
D. По значению переменных сделаем заключение о решении задачи. Получили три решения.
| 1-й урок – математика 2-й урок – литература 3-й урок – информатика 4-й урок – физкультура | 1-й урок – математика 2-й урок – информатика 3-й урок – литература 4-й урок – физкультура | 1-й урок – информатика 2-й урок – математика 3-й урок – литература 4-й урок – физкультура |
Схема перехода от практической задачи к компьютерной
модели


 Реальный объект Системный анализ Логическая функция (информационная модель) Компьютерная модель (программа для выбранного исполнителя).
Реальный объект Системный анализ Логическая функция (информационная модель) Компьютерная модель (программа для выбранного исполнителя).
Поэтапное решение этих задач приводит к необходимости либо уточнять некоторые понятия математической логики, либо вводить эти понятия.
2. Элементы математической логики
Представление логической структуры учебного материала по данной теме
Всякий учебный материал имеет свою логическую структуру. Осознание этой структуры – одно из эффективных средств внесения элементов творчества в учебную деятельность учащихся. Творить – значит создавать новое. Это новое может быть не только неизвестным ученику фактом, а новым приемом мыслительной деятельности, открытием связей между явлениями, нахождение логической структуры учебного материала. В представленной логико-структурной схеме (рис. 39) учебного материала данной темы указаны компоненты и их взаимосвязь, выстроена иерархия понятий, установлена последовательность их введения.
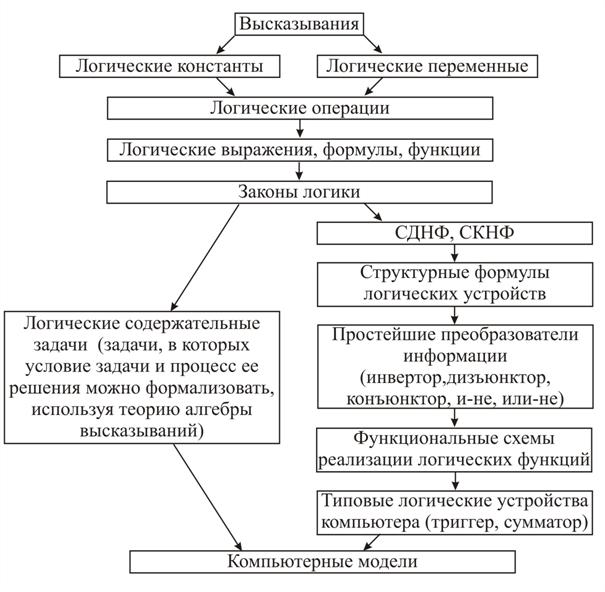
|
| Рис. 39 |
2.1. Логические операции
Высказывание – повествовательное предложение, относительно которого можно сказать, истинно оно или ложно. Логические константы – это константы, которые принимают два значения, называемые "истиной" и "ложью". Принято истинное значение обозначать TRUE или 1, а ложное – FALSE или 0. Высказывания обозначаются заглавными латинскими буквами (A, B, …). Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значением истинности исходных высказываний (табл. 3).
Инверсия – образуется из высказывания с помощью добавления частицы «не» к сказуемому или использования оборота речи «неверно, что…». Обозначается: 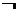 ,
,  , not. Инверсия высказывания истинна, когда высказывание ложно, и ложна, когда высказывание истинно.
, not. Инверсия высказывания истинна, когда высказывание ложно, и ложна, когда высказывание истинно.
| Инверсия | |
| А | 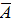
|
Конъюнкция – логическое произведение – образуется соединением двух высказываний в одно с помощью знаков операции &, 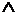 , •, и, and. Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно высказывание ложно.
, •, и, and. Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно высказывание ложно.
Дизъюнкция – логическое сложение – образуется соединением двух высказываний в одно с помощью знаков операции  , +, или, or. Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно высказывание истинно.
, +, или, or. Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно высказывание истинно.
Исключающее ИЛИ – образуется соединением двух высказываний в одно с помощью знаков операции ", Å, xor. Исключающее ИЛИ двух высказываний истинно тогда и только тогда, когда одно высказывание ложно и одно высказывание истинно, и ложно в противном случае.
Импликация – образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…». Обозначается:  ,
, 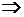 . Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное высказывание.
. Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное высказывание.
Таблица 3
Таблица истинности логических операций
| А | В | А&В | 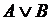
| 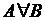
| 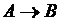
| 
|
Эквивалентность – образуется соединением двух высказываний в одно с помощью оборота речи «… тогда и только тогда, когда …». Обозначается: 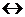 ,
, 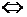 , =. Эквивалентность двух высказываний истинна тогда и только тогда, когда оба высказывания истинны или оба высказывания ложны.
, =. Эквивалентность двух высказываний истинна тогда и только тогда, когда оба высказывания истинны или оба высказывания ложны.
Используя основные логические операции, можно построить более сложные высказывания – логические выражения, например,
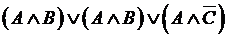 ,
, 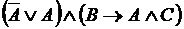 .
.
Логические выражения строятся из простых высказываний А, В, C,..., знаков логических операций и скобок. При отсутствии скобок первой всегда выполняется операция отрицания, затем конъюнкция, дизъюнкция и далее импликация и эквиваленция в порядке следования.
Логическая функция – это функция, определенная на множестве истинностных значений и принимающая значение из того же множества. Например,
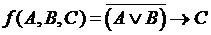 .
.
2.2. Построение таблицы истинности
Алгоритм построения таблицы истинности
· Определи количество строк в таблице по формуле 2 k, где k количество логических переменных в выражении.
· Определи количество столбцов в таблице – количество логических переменных плюс количество логических операций.
· Построй таблицу истинности. Обозначь столбцы, заполни столбцы значений исходных логических переменных всевозможными различными наборами значений из 2 элементов (0,1) по k, где k – количество данных логических переменных (размещения с повторением из 2 элементов (0 или 1) по k).
· Заполни таблицу до конца, выполняя логические операции в заданной в выражении последовательности (табл. 4).
Составление таблиц истинности логических функций
с использованием систем программирования
Обозначение истинности выражений в языках программирования дано в табл. 4.
Таблица 4
| Значение истинности | Запись значений | |||
| Turbo Pascal | Turbo Delphi | Visual Basic | QBasic | |
| Ложь | false | false | false | |
| Истина | true | true | true | -1 |
Программы построения таблиц истинности логических операций: A and B, A or B, not A, A xor B.
Turbo Pascal
program table1;
var A,B: boolean;
begin
writeln ('A ':7, 'B ':7, ' A and B ':7, 'not A ':7, 'A or B ':7,'A xor B ':7);
for A:=false to true do
for B:=false to true do
begin
writeln (A:7, B:7,(A and B):7, not A:7,(A or B):7, (A xor B):7);
end; end.
QBasic
REM table
CLS
PRINT USING"\ \"; " A";" B";" A and B";" not A";"A OR B";" A XOR B"
FOR A = 0 TO -1 STEP -1
FOR B = 0 TO -1 STEP -1
PRINT USING "########"; A; B; A and B; not A; A or B; A xor B
NEXT B, A
END
| Turbo Delphi procedure TForm1.Button1Click (Sender: TObject); const n=6; var a,b:boolean; i,j:1..n; begin with stringgrid1 do begin Cells[1,0]:='A'; Cells[2,0]:='B'; Cells[3,0]:='A and B'; Cells[4,0]:='not A'; Cells[5,0]:='A or B'; Cells[6,0]:='A xor B'; end; i:= 1; For a:= false To true do For b:= false To true do begin with StringGrid1 do begin j:= 1; Cells[j, i]:= BoolToStr(a,true); j:= 2; Cells[j, i]:= BoolToStr(b,true); j:= 3; Cells[j, i]:= BoolToStr(a And b, true); j:= 4; Cells[j, i]:= BoolToStr(Not a,true); j:= 5; Cells[j, i]:= BoolToStr(a Or b, true); j:= 6; Cells[j, i]:= BoolToStr(a Xor b, true); i:= i + 1; end; end; end; | Visual Basic.Net Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click Dim a, b As Boolean Dim i, j, k, l As Integer With (DataGridView1) .Rows.Add(3) .Columns(0).HeaderText = "A" .Columns(1).HeaderText = "B" .Columns(2).HeaderText = "A and B" .Columns(3).HeaderText = "not A" .Columns(4).HeaderText = "A or B" .Columns(5).HeaderText = "A xor B" End With i = 0 For k = 0 To -1 Step -1 If k = -1 Then a = True Else a = False For l = 0 To -1 Step -1 If l = -1 Then b = True Else b = False With DataGridView1 j = 0:.Item(j, i).Value = a j = 1:.Item(j, i).Value = b j = 2:.Item(j, i).Value = a And b j = 3:.Item(j, i).Value = Not a j = 4:.Item(j, i).Value = a Or b j = 5:.Item(j, i).Value = a Xor b i = i + 1 End With Next Next End Sub |
Результат формирования таблиц
| Delphi | Visual Basic.NET |
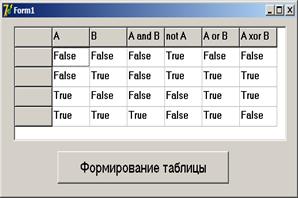
| 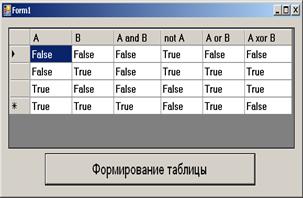
|
2.3. Упрощение логических выражений
Алгоритмы получения СДНФ И СКНФ по таблице истинности
| СДНФ | СКНФ |
| 1. Отметьте звёздочкой строки таблицы, в которых стоят единицы в столбце значений логической функции. 2. Для каждой выделенной строки выпишите конъюнкцию всех переменных: если значение переменной в данной строке равно 1, то в конъюнкцию включите саму эту переменную, а если 0, то её отрицание. 3. Все конъюнкции свяжите в дизъюнкцию. Получите СДНФ исследуемой функции. | 1. Отметьте звёздочкой строки таблицы, в которых стоят нули в столбце значений логической функции. 2. Для каждой выделенной строки выпишите дизъюнкцию всех переменных: если значение переменной в данной строке равно 0, то в дизъюнкцию включите саму эту переменную, а если 1, то её отрицание. 3. Все дизъюнкции свяжите в конъюнкцию. Получите СКНФ исследуемой функции |
Основные законы логики
Законы коммутативности
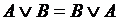 , , 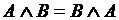 Законы дистрибутивности
Законы дистрибутивности
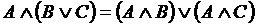 , ,
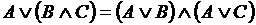 Важные формулы ( I – истина, L – ложь).
Важные формулы ( I – истина, L – ложь).
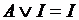 , , 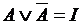 , , 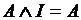 , ,
 , , 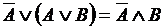 , ,
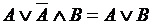 , ,  . .
| Законы ассоциативности
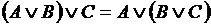 , ,
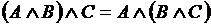 .
Законы идемпотентности .
Законы идемпотентности
 , , 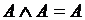 .
Законы поглощения .
Законы поглощения
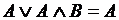 , , 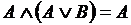 .
Законы де Моргана .
Законы де Моргана
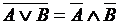 , , 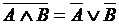 . .
|
Инфолюция
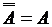 , , 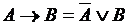 , ,
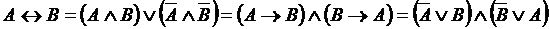
|
3. Базовые логические элементы функциональных схем, реализующие логические операции
Для составления функциональных схем используют базовые логические элементы, простейшие преобразователи информации[8], являющиеся графическими представлением часто используемых логических операций, табл. 5. Преобразователи могут иметь один или несколько входов и только один выход. По входам преобразователь получает информацию, на выходах демонстрирует результат преобразования. На входах и выходах появляются сигналы только булевского типа. Сигнал, выработанный одним логическим элементом, можно подавать на вход другого элемента, что даёт возможность образовывать цепочки из отдельных логических элементов. Каждая цепочка из логических элементов, где выходы одних логических элементов являются входами других, реализует определённую логическую функцию. Графическое представление логической функции называется функциональной схемой функции.
Таблица 5
| Инвертор | Конъюнктор | Дизъюнктор |

| 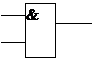
| 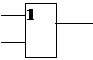
|
| Элемент XOR | Элемент Вебба, И – НЕ | Элемент Шеффера, ИЛИ – НЕ |
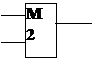
| 
| 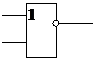
|
4. Информационные и компьютерные модели решения логических содержательных задач
Решение логических содержательных задач – это практикум в составлении информационных и компьютерных моделей, это практикум в формировании умений и навыков формализации условия задачи и процесса её решения. Существуют различные способы решения логических содержательных задач, различные способы составления информационных моделей: алгебраический, табличный, графический и др. Каждый из этих методов обладает своими достоинствами. Так, например, при применении алгебраического метода наиболее трудным считается перевод текста задачи на язык формул, но далее, если вы знаете методы упрощения логических выражений или умеете составлять таблицы истинности на компьютере, решение задачи сводится к формальным преобразованиям и приводит сразу к ответу, который остается лишь расшифровать, исходя из принятых вами обозначений.
Табличный метод очень нагляден, но предназначен для решения только определенного класса задач, он требует анализа находящейся в таблице информации, умения сравнивать и сопоставлять.
Граф позволяет наглядно представить связи между объектами, о которых идет речь в задаче, и определить, какие из них не противоречат условиям задачи.
Метод диаграмм Эйлера — Венна позволяет графически решать математические задачи на основе применения теории множеств.
Как правило, задачу можно решить несколькими способами (методами). Чтобы выбрать наиболее простой и эффективный способ для каждой конкретной задачи, необходимо знать все эти способы.
4.1. Алгебраический метод решения логических задач
Задача. Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая удивительную находку, каждый высказал по два предположения:
Алеша сказал: «Это сосуд греческий и изготовлен в V веке». Боря сказал: «Это сосуд финикийский и изготовлен в III веке». Гриша сказал: «Это сосуд не греческий и изготовлен в IV веке». Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
Указание. Используйте поэтапное решение задачи с составлением информационных и компьютерных моделей, предложенное на с. 104.
Решение
A. Реализуем первый и второй этапы решения задачи. В условии даны высказывания школьников и учителя. Введём следующие обозначения: G – «Это сосуд греческий»; F – «Это сосуд финикийский»; 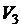 – «Сосуд изготовлен в III в.»;
– «Сосуд изготовлен в III в.»; 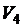 – «Сосуд изготовлен в IVв.»;
– «Сосуд изготовлен в IVв.»; 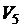 – «Сосуд изготовлен в V в.»
– «Сосуд изготовлен в V в.»
B. Условие задачи запишем в выбранных обозначениях, формализуем условие задачи. Из высказывания учителя следует, что Алеша прав только в чем-то одном: или 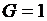 , или
, или 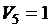 . Таким образом, тождественно истинным будет высказывание –
. Таким образом, тождественно истинным будет высказывание – 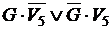 . Аналогично из слов Бори и учителя следует, что
. Аналогично из слов Бори и учителя следует, что 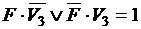 , а из слов Гриши и учителя –
, а из слов Гриши и учителя – 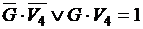 . Кроме того, ясно, что сосуд может быть изготовлен только в одном из веков и только в одной из стран. Эти условия можно записать так:
. Кроме того, ясно, что сосуд может быть изготовлен только в одном из веков и только в одной из стран. Эти условия можно записать так:
Date: 2015-07-17; view: 621; Нарушение авторских прав