
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Требования к уровню подготовки учащихся 5 page
|
|
3.2. Матрица инцидентности
Рассмотрим представление графа с помощью матрицы I, отражающей инцидентность вершин и ребер (дуг). Опишем матрицы с использованием двумерного массива.
I: array [1..n, 1..m] of 0..1; (для неориентированного графа);
I: array [1..n, 1..m] of –1..1; (для ориентированного графа).
Неориентированный граф:
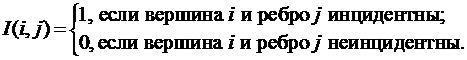
Если в графе нет петель, то в каждом столбце матрицы инцидентности будет ровно 2 единицы. Наличие столбца с 1 единицей означает, что в графе имеется петля
Ориентированный граф:

Для ориентированного графа петлю, то есть дугу вида 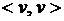 удобно представить в строке v значением, например 2.
удобно представить в строке v значением, например 2.
Примеры представления графов матрицей инцидентности
Матрица инцидентности для неориентированного графа (см. рис. 28)
| a | b | c | d | e | f | g | h | |
Матрица инцидентности для ориентированного графа (см. рис. 31)
| a | b | c | d | e | f | g | h | |
| -1 | -1 | |||||||
| -1 | ||||||||
| -1 | -1 | -1 | ||||||
| -1 | ||||||||
| -1 | ||||||||
С алгоритмической точки зрения матрица инцидентности является плохим представлением графа. Оно требует размер памяти, пропорциональный nm, и имеет не удобный доступ к информации. Ответы на вопросы, существует ли дуга < U,V >, к каким вершинам ведут рёбра из U, требуют в худшем случае m шагов.
3.3. Список рёбер графа
Более экономным в отношении памяти, когда m гораздо меньше 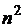 , является метод представления графа перечислением рёбер графа в виде пар соответствующих вершин. В языках программирования такому представлению графа соответствует представление графа в виде массива
, является метод представления графа перечислением рёбер графа в виде пар соответствующих вершин. В языках программирования такому представлению графа соответствует представление графа в виде массива 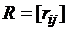 размера
размера 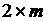 .
.
R: array [1..2, 1..m] of 1..n;
R [1, i] – первая вершина (начало) ребра (дуги) a;
R [2, i] – вторая вершина (конец) ребра (дуги) a. .
Примеры представления графов списком рёбер
Представление неориентированного графа списком рёбер (см. рис. 28)
| a | h | g | b | c | e | f | d | |
Представление ориентированного графа списком рёбер (см. рис. 31)
| a | g | b | h | e | f | c | d | |
Очевидно, что объём памяти для хранения массива пропорционален 2 m. Неудобством при представлении графа в виде списка рёбер является большое число шагов – порядка m в худшем случае, необходимых для получения множества вершин, к которым ведут рёбра из рассматриваемой вершины. Для решения такой задачи нужно упорядочить множество пар лексикографически и применить двоичный поиск.
Задача 10. Разработайте и реализуйте программы ввода описаний графа, заданного диаграммой, в память компьютера, используя все рассмотренные способы[4]. Для контроля корректности ввода предусмотрите в программе вывод каждого описания на экран.
Задача 11. Разработайте и реализуйте программу моделирования процессов перехода между каждыми двумя способами представления графа, рассмотренными выше, оцените вычислительную сложность каждой процедуры.
4. Поиск пути в графе
Задача 12. Поиск пути в лабиринте. Лабиринт представлен как система комнат, некоторые из которых связаны между собой коридорами. Найдите маршрут выхода из лабиринта, представленного на рис. 34, путь от начальной комнаты (1) до конечной комнаты (11). Разработайте информационную и компьютерную модели рассматриваемого процесса отыскания маршрута выхода из лабиринта.
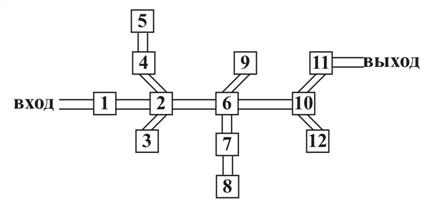
|
| Рис. 34 |
Указания к решению. Определим средства, которые имеются в распоряжении путешественника в лабиринте. Будем предполагать, что он знает номер той комнаты, в которую вошел, номер комнаты, в которую ведет обозреваемый им коридор. Путешественник знает те комнаты, в которых уже побывал, а в случае необходимости может проделать часть пройденного пути в обратном порядке. При поиске интересующего пути необходимо руководствоваться следующими правилами:
а) при движении вперед из той комнаты, в которой находишься, всегда идти в комнату, в которой ещё не побывал (если таких комнат несколько, то выбрать комнату с наименьшим номером);
б) если из данной комнаты нельзя пройти в комнату, в которой еще не бывал, то нужно вернуться в предыдущую комнату.
Задача 13. Маршрут экскурсовода в зоопарке. На рис. 35 представлена схема зоопарка. Вершины схемы – вольеры для зверей, рёбра – дорожки между вольерами. Разработайте компьютерную модель процесса отыскания маршрута, по которому экскурсовод мог бы провести посетителей, показав им всех зверей и не проходя более одного раза ни одного участка пути.
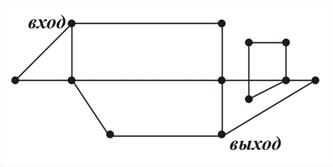
|
| Рис. 35 |
Для того чтобы найти решение поставленных задач, надо уметь находить пути в графе от одной вершины к другой, то есть научиться обходить граф. Существует много алгоритмов на графах, в основе которых лежит систематический перебор вершин графа такой, что каждая вершина графа просматривается точно один раз, такие алгоритмы называются поиском пути в графе, или обходом графа. Рассмотрим два метода поиска пути в графе – метод поиска в глубину (англ. depth first search) и метод поиска в ширину (англ. breadth first search). Эти методы входят в основные методики проектирования алгоритмов на графах.
4.1. Метод поиска пути в глубину (для неориентированного графа)
Просмотр вершин графа начинается с некоторой вершины V. Выбирается вершина U, смежная с V, не просмотренная ранее; процесс повторяется с вершиной U. Если на очередном шаге мы работаем с вершиной G, и нет вершин, смежных с G, не просмотренных ранее, то возвращаемся из G к вершине Q, из которой попали в G. Далее выбираем вершину, смежную с Q, не просмотренную ранее, и т. д. Если по возвращении мы попали в вершину V, и нет вершин, смежных с ней, и не просмотренных ранее, то просмотр закончен. Другими словами, поиск в глубину из вершины V основывается на поиске в глубину из всех вершин, смежных с V.
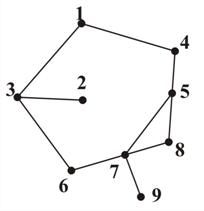
|
| Рис. 36 |
Пример последовательности анализируемых вершин при просмотре графа в глубину (рис. 36), начиная от вершины 1: 1, 3, 2, 6, 7, 5, 4, 8, 9.
Программы обхода графа в глубину
Описание данных
| A – матрица смежности, A:array[1..n,1..n] of 0..1; Apex– массив, где хранятся просмотренные вершины, Apex:array[1..n] of 1..n; Nnew – массив, хранящий сведения о каждой вершине (просмотрена она или нет) | Nnew:array[1..n] of boolean; St – стек вершин, запомненных для просмотра (представленный в программе как массив) Uk – указатель на позицию элемента массива (вершину стека) для записи и извлечения элемента. |
Исходные данные – матрица смежности графа (см. рис. 36).
Результат – последовательность вершин при обходе графа в глубину.
| { нерекурсивная программа обхода графа в глубину } program graf_depth; uses crt; const n=9; type mas=array[1..n] of 1..n; mas1=array[1..n,1..n] of 0..1; const a:mas1=((0,0,1,1,0,0,0,0,0), (0,0,1,0,0,0,0,0,0), (1,1,0,0,0,1,0,0,0), (1,0,0,0,1,0,0,0,0),(0,0,0,1,0,0,1,1,0), (0,0,1,0,0,0,1,0,0),(0,0,0,0,1,1,0,1,1), (0,0,0,0,1,0,1,0,0),(0,0,0,0,0,0,1,0,0)); var apex:mas;st:mas; v:byte; i,m:integer; nnew:array[1..n] of boolean; procedure ver(v:byte); var uk,t,j:byte; p:boolean; begin uk:=1; apex[m]:=v; nnew[v]:=false; st[uk]:=v; while uk<>0 do begin t:=st[uk]; p:=false; j:=1; repeat if (a[t,j]<>0) and (nnew[j]) then p:=true else inc(j); until (p) or (j>n); | if p then begin uk:=uk+1; st[uk]:=j; nnew[j]:=false; m:=m+1; apex[m]:=j; end else uk:=uk-1; end; end; begin clrscr; for i:=1 to n do nnew[i]:=true; v:=1;m:=1; ver(v); for i:=2 to n do if nnew[i] then ver(i); for i:=1 to n do write(apex[i]:4); end. |
| { рекурсивная программа поиска в глубину } program graf_depth1; uses crt; const n=9; type mass=array[1..n,1..n]of integer; mass1=array[1..n] of boolean; const a:mass=((0,0,1,1,0,0,0,0,0), (0,0,1,0,0,0,0,0,0), (1,1,0,0,0,1,0,0,0), (1,0,0,0,1,0,0,0,0),(0,0,0,1,0,0,1,1,0), (0,0,1,0,0,0,1,0,0),(0,0,0,0,1,1,0,1,1), (0,0,0,0,1,0,1,0,0),(0,0,0,0,0,0,1,0,0)); var i,v,m:integer; sw:mass1; apex:array[1..n] of integer; procedure ser(v:integer); var i,j:integer; | begin m:=m+1; sw[v]:=true; write(v); apex[m]:=v; for j:=1 to n do if (a[v,j]<>0) and (not sw[j]) then ser(j); end; begin for i:=1 to n do sw[i]:=false; clrscr; write('введите первую вершину для просмотра'); readln(v); ser(v); m:=0; for i:=1 to n do if not sw[i] then ser(i); end. |
4.2. Поиск пути в ширину в неориентированном графе
Просмотр вершин графа начинается с некоторой вершины V – первой текущей вершины. Далее рассматриваются все вершины, смежные с выбранной текущей и не просмотренные ранее. Выбирается следующая текущая вершина, принцип выбора которой такой: выбирается та вершина, которая была ранее всех просмотрена, но не выбиралась текущей. Процесс просмотра вершин заканчивается, когда все просмотренные вершины будут использованы как текущие.
Пример последовательности анализируемых вершин при просмотре графа (см. рис. 36) в ширину, начиная от вершины 1: 1, 3, 4, 2, 6, 5, 7, 8, 9.
Программа обхода графа в ширину
Описание данных
| A – матрица смежности, A:array[1..n,1..n] of 0..1; Apex– массив, где хранятся просмотренные вершины, Apex:array[1..n] of 1..n; | Uk1– указатель на позицию постановки элемента (вершины) в очередь. Пример. Uk1:=5; Turn[Uk1]:=’A’; В очередь Turn на пятую позицию поставлена вершина A. |
| Nnew – массив, хранящий сведения о каждой вершине (просмотрена она или нет), Nnew:array[1..n] of boolean; Turn – очередь вершин, поставленных на просмотр (представленная в программе как массив). | Uk2 – указатель на позицию извлечения элемента массива (вершины) из очереди. Пример. Uk2:=3; z:=Turn[Uk2]; Из очереди Turn с третьей позиции извлекается вершина для анализа |
Исходные данные – матрица смежности графа (см. рис. 36). Результат – последовательность вершин при обходе графа в ширину.
| program graf; const n=9; type mas=array[1..n] of 1..n; mas1=array[1..n,1..n] of 0..1; const a:mas1=((0,0,1,1,0,0,0,0,0), (0,0,1,0,0,0,0,0,0), (1,1,0,0,0,1,0,0,0), (1,0,0,0,1,0,0,0,0),(0,0,0,1,0,0,1,1,0), (0,0,1,0,0,0,1,0,0),(0,0,0,0,1,1,0,1,1), (0,0,0,0,1,0,1,0,0),(0,0,0,0,0,0,1,0,0)); var apex, st:mas; v, i, m, k, j: byte; nnew:array[1..n] of boolean; procedure breadth(v:byte;m1:1..n); var uk1, i,t:1..n;turn:array[1..n] of 1..n; uk2:0..n; begin uk1:=1;uk2:=0;turn[uk1]:=v; apex[m1]:=v; nnew[v]:=false; while uk2<>uk1 do begin uk2:=uk2+1; t:=turn[uk2]; | for i:=1 to n do if (a[t,i]<>0) and (nnew[i]) then begin uk1:=uk1+1; turn[uk1]:=i; nnew[i]:=false; m1:=m1+1; apex[m1]:=i;{pred[i]:=t;} end; end; end; begin write('Введите начальную точку '); readln(v); for i:=1 to n do nnew[i]:=true; m:=1; breadth(v,m); for i:=2 to n do if nnew[i] then breadth(i,m); for i:=1 to n do write(apex[i]:4); end. |
Замечания
1. Покажем, что алгоритмы просматривают каждую вершину в точности 1 раз. Каждая вершина просматривается не более одного раза, так как просматривается только вершина V, для которой Nnew[V]=true. Алгоритм начинает поиск поочередно от каждой еще не просмотренной вершины. Следовательно, просматриваются все вершины графа, даже не обязательно связного.
2. Конечность алгоритмов поиска в глубину и в ширину. Всего в St может попасть не более n вершин при поиске в глубину. На каждом шаге процедуры одна вершина t удаляется из стека, если для нее нет смежной. Следовательно, алгоритм завершит работу, когда стек станет пустым. Аналогичные рассуждения для поиска в ширину. Сложность алгоритмов поиска пути графа в глубину и в ширину равна O(n+m).
3. Оба вида поиска в графе могут быть использованы для нахождения пути между фиксированными вершинами U и V. Достаточно начать поиск пути в графе с вершины V и вести его до момента посещения вершины U. Преимуществом поиска в глубину является тот факт, что в момент посещения вершины U стек содержит последовательность вершин, определяющих путь от V к U. Это очевидно, так как каждая вершина, помещаемая в стек, является смежной с вершиной, находящейся в вершине стека.
Используя метод поиска в ширину, можно получить кратчайший путь, так как в очередь помещены сначала вершины, находящиеся на расстоянии 0 от V, то есть сама вершина V. Затем вершина, находящаяся на расстоянии 1 от вершины V, и т. д. Зная предыдущую вершину U, а также предыдущие вершины для каждой вершины графа G, мы можем найти путь от V к U. Для этого обход в ширину необходимо начать с вершины V, а в программу достаточно вставить оператор pred[i]:= t; (в программе этот оператор выделен в фигурные скобки), и в конце программы добавить нижерасположенный фрагмент, описав недостающие переменные: k – типa byte, массивы pred[1:n] и z[1:n] – типа mass, u – типа byte, где u – конечная вершина искомого кратчайшего пути.
| writeln; write('введите конечную вершину пути '); readln(u); i:=u; k:=1;z[k]:=u; while i<>v do | begin i:=pred[i]; k:=k+1; z[k]:=i; end; for i:=k downto 1 do write(z[i]:4); |
Задача 14. Разработайте и реализуйте программы, моделирующие процессы поиска пути в ориентированном графе, поиска в глубину и поиска в ширину. Граф задается матрицей смежности или построением диаграммы в графическом окне выбранной системы программирования.
Задача 15. Составьте компьютерную модель процесса поиска пути в неориентированном графе, поиск в ширину, если достигнутая вершина помещается не в очередь, а в стек. Оцените вычислительную сложность программы.
Матрица достижимости
Если существует путь от вершины V к U, то говорят, что U достижима из V. Определим матрицу достижимости – это матрица D размера 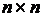 .
.
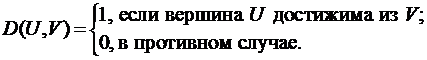
Программа формирования матрицы достижимости
Пусть граф G задан матрицей смежности, матрица D – матрица достижимости.
| Uses crt; Const n=9; Type mass=array[1..n,1..n] of 0..1; Const a:mass=((0,0,1,1,0,0,0,0,0), (0,0,1,0,0,0,0,0,0), (1,1,0,0,0,1,0,0,0), (1,0,0,0,1,0,0,0,0),(0,0,0,1,0,0,1,1,0), (0,0,1,0,0,0,1,0,0),(0,0,0,0,1,1,0,1,1), (0,0,0,0,1,0,1,0,0),(0,0,0,0,0,0,1,0,0)); Var D:mass; i,j:integer; Procedure reach; Var i,j,k:byte; S,T:set of 1..n; Begin for i:=1 to n do begin T:=[i]; repeat S:=T; | for k:=1 to n do if k in S then for j:=1 to n do if A[k,j]<>0 then T:=T+[j]; until S=T; for j:=1 to n do if j in S then D[i,j]:=1; end; end; Begin Clrscr; reach; for i:=1 to n do begin for j:=1 to n do write(D[I,j]:4); writeln; end; End. |
Вопрос. Каким свойством обладает матрица достижимости связного неориентированного графа?
Замечание. Если вершины графа перенумеровать соответствующим образом, то связные компоненты графа G соответствуют состоящим из единиц квадратным подматрицам матрицы достижимости.
5. Вопросы и задания к семинарским занятиям
Тема «Графы и компьютерное моделирование»
Перефразируйте задания 1 – 6 главы 1, сформулировав предлагаемые задания и вопросы для рассматриваемой темы «Графы и компьютерное моделирование». Выполните задания 1 – 6, ответьте на вопросы, поставленные в этих заданиях. Доложите результаты своей работы в студенческой аудитории в форме презентации.
7. Подберите мотивационные задачи для введения понятия «граф» и демонстрации удобства языка теории графов для описания информационных и компьютерных моделей практических задач. Разработайте методику использования выбранных мотивационных задач на уроках по данной теме. Апробируйте свои разработки в студенческой аудитории.
8. Отберите содержание учебного материала, разработайте методику изложения выбранного материала по предложенным ниже темам на выбранной ступени непрерывного курса изучения информатики. Разработайте соответствующие фрагменты уроков. Апробируйте в студенческой аудитории один из фрагментов урока.
· Введение основных понятий теории графов (граф, вершина графа, ребро графа, дуга графа, ориентированный и неориентированный граф, смежные вершины и т. д.).
· Машинное представление графов (матрица инцидентности, матрица смежности, перечень ребер, списки связей или списки инцидентностей).
· Связность графа, путь в графе, цикл, элементарный цикл, поиск пути в графе в глубину, поиск пути в графе в ширину, сравнение обхода вершин графа разными способами.
· Эйлеров путь, эйлеров цикл, алгоритм нахождения эйлерова цикла.
· Алгоритм определения уникурсальной линии.
6. Лабораторно-практическая работа
Тема «Графы и компьютерное моделирование»
Задание 1. Отберите содержание темы для решения предложенных в данной главе задач 4, 8-14, разработайте методики обучения школьников поиску решения предложенных задач, оформите решения задач. Мотивируйте свой выбор методик поиска решения конкретных задач. Апробируйте разработанные методики поиска решения задач в студенческой аудитории.
Для выполнения заданий 2 и 3 разработайте и реализуйте с использованием выбранного исполнителя учебный проект в виде компьютерной модели, рассмотрев все этапы составления компьютерных моделей. Подготовьте проекты к защите.
Задание 2. В некоторой стране 110 городов, между некоторыми из них летают самолеты. Авиатрассы расположены так, что из любого города можно перелететь в другой (возможно с пересадками), известна цена перелёта из города V в город U. Разработайте компьютерную модель процесса нахождения:
· всех маршрутов из города V в город U, делая не более одной пересадки, и цены каждого из этих маршрутов;
· всех маршрутов из города V в город U с одной пересадкой в порядке возрастания цены маршрута;
· всех маршрутов из города V в город U ровно с двумя пересадками;
· всех маршрутов из города V в город U с двумя пересадками, в порядке убывания цены маршрута;
· всех маршрутов из города V в город U, делая не более трёх пересадок.
Задание 3. Разработайте учебный проект в виде компьютерной модели, позволяющей получить остовные связные деревья минимального веса для графов с пятью вершинами. Граф в виде схемы задайте в графическом поле, а матрицу смежности, соответствующую заданной схеме, выведите в элемент управления, представляющий собой таблицу [16].
7. Самостоятельная работа
Тема «Графы и компьютерное моделирование»
Для выполнения заданий 1, 2 разработайте и реализуйте с использованием выбранного исполнителя учебные проекты в виде компьютерных моделей, рассмотрев все этапы составления компьютерных моделей. Проекты подготовьте к защите.
Задание 1. Проект «Владимирское метро». Спроектируйте информационную и компьютерную модели линий и станций Владимирского метро, учитывающую время в пути между соседними станциями и примерное время, которое тратится на пересадки.
Задание 2. Разработайте и реализуйте на выбранном языке программирования компьютерную модель справочного электронного табло для пассажиров одной фиксированной станции проекта «Владимирское метро». Продумайте оформление табло, возможность получения ответов на актуальные вопросы пассажиров.
Выполните задания 3, 4, 5. Проделанную и оформленную работу подготовьте для защиты.
Задание 3. Составьте поурочный план изучения данной темы по предмету «Информатика и ИКТ» на одной из ступеней непрерывного курса изучения информатики.
Задание 4. Разработайте тематику, содержание, методы и приёмы проведения лабораторных работ по теме «Графы и компьютерное моделирование» на каждой ступени непрерывного курса изучения информатики.
Задание 5. Разработайте сценарии программ (демонстрационных, обучающих, тренажеров, контролирующих) по данной теме и реализуйте их на одном из языков программирования.
Глава 3. Логические информационные и компьютерные модели
| «Ибо это недостойно совершенства человеческого, подобно рабам тратить часы на вычисления» Лейбниц |
Самой мощной движущей силой развития информатики является стремление освободить человека от бремени однообразной утомительной умственной работы, переложив её на электронно-вычислительную технику. Сфера применения электронно-вычислительной техники обширна и практически охватывает все области человеческой деятельности. Только познав «внутреннюю жизнь» электронно-вычислительной техники (компьютера), подчинённую строгим законам логики и таких наук, как физика, химия, математика, можно полноценно использовать её (его) для решения практических задач. Глубокая идейная связь, столь характерная для современного развития логики и информатики, находит своё выражение во многих новых направлениях, имеющих практическое значение.
Рассмотрим некоторые аспекты изучения темы «Логические информационные и компьютерные модели» в школьном предмете «Информатика и ИКТ». Учебный материал этой темы даёт возможность для реализации основной задачи курса информатики, направленной на развитие у обучаемых информационной культуры. Это формирование умений, необходимых для осуществления всех этапов процесса исследования, а также приобретение субъективного опыта обучаемого в познавательной деятельности.
Выполнение заданий по теме формирует умения и навыки в овладении основным методом познания окружающей действительности – методом моделирования и, в частности, методом компьютерного моделирования. Способствует развитию навыков логического обоснования выводов из практических задач, использования аналитико-синтетического метода при нахождении решения поставленной задачи, позволяет вести обучение на достаточном уровне сложности, что обусловливает необходимость повышения роли теоретических знаний в содержании образования, умелого применения полученных знаний в новой обстановке; позволяет решать задачи с продолжением. Многообразие способов решения предложенных задач позволяет учащемуся выбрать интересный и посильный для него метод. Ценность теории определяется тем, насколько она применима на практике. Содержание темы, с одной стороны, вбирает основные понятия, опорные знания по математической логике, с другой – способствует сознательному использованию компьютерного моделирования при решении практических задач.
1. От практических задач к компьютерным моделям
При изучении темы «Логические информационные и компьютерные модели» можно предложить рассмотреть такие мотивационные задачи.
Задача 1. Пусть в некотором университете проходит в несколько туров конкурс танца. Четырьмя членами жюри (A, B, C, D) решается вопрос о допуске того или иного участника к следующему туру. Решение положительно тогда и только тогда, когда хотя бы трое членов жюри высказываются за допуск, причем среди них обязательно должен быть председатель жюри A.
Задание. Разработайте электронное устройство для голосования и реализуйте это устройство с использованием выбранного вами исполнителя, включая программы «Конструктор логических схем», для составления компьютерной модели.
Для создания компьютерной модели необходимо разработать информационные модели: составить таблицу истинности, структурную формулу, соответствующую разрабатываемому устройству, функциональную схему.
Решение.
а) Составим таблицу истинности, соответствующую работе жюри:
| А | В | С | D | F (А, В, С, D) |
| 1* | ||||
| 1* | ||||
| 1* | ||||
| 1* |
б) Составим структурную формулу, соответствующую разрабатываемому устройству.
Date: 2015-07-17; view: 722; Нарушение авторских прав