
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Требования к уровню подготовки учащихся 1 page
|
|
Учащиеся должны понимать:
· моделирование – это метод познания окружающей действительности, практической деятельности;
· сущность технологического подхода к решению задачи;
· смысл модели как заменителя объекта в процессе решения практической задачи;
· суть формализации как основного этапа моделирования;
· суть адекватности как соответствия модели моделируемому объекту и целям моделирования;
· компьютерный эксперимент имеет и существенные преимущества, и определенные ограничения перед натурным экспериментом;
· в процессе формализации решения данной задачи возникает три вида объектов: исходный информационный объект, итоговый информационный объект, информационный процесс преобразования исходного информационного объекта в итоговый;
· управляя исполнителями, учащиеся на самом деле работают с их компьютерными моделями;
· отладка и тестирование программы, реализующей алгоритм решения задачи, – это проведение компьютерного эксперимента.
Учащиеся должны знать:
· общую схему информационной технологии решения задачи;
· виды информационных моделей;
· цели и этапы проведения компьютерного эксперимента.
Учащиеся должны уметь:
· выделять среди свойств данного объекта существенные свойства с точки зрения целей моделирования;
· строить модели задачи (выделять исходные данные, результаты, устанавливать соотношения между ними, отражать эти отношения с помощью формул, таблиц, графов, функциональных схем);
· раскрывать содержание понятия «информационная модель» на примерах;
· анализировать задачу и определять, какая часть может быть поручена компьютеру, а какая требует человеческой интуиции и творческих способностей к принятию решения;
· по постановке задачи определять возможность использования компьютерных программ для ее решения;
· интерпретировать таблицы, диаграммы, графы, схемы;
· строить функциональные схемы типовых логических устройств;
· проводить компьютерный эксперимент для построенных моделей;
· оценивать адекватность построенной модели объекту-оригиналу и целям моделирования;
· на каждом шаге решения задачи критически осмысливать работу компьютера и определять правильность выбранных методов решения.
Для работы с компьютерными моделями можно выбрать следующие инструменты:
· системы программирования: Ершол, QBasic, Turbo Pascal, Visual Basic. Net, Turbo Delphi, Visual C#, Visual J# и др.;
· электронные таблицы (Microsoft Office Excel);
· системы управления базами данных (Microsoft Office Access);
· специализированные математические пакеты (Mathcad);
· другие средства.
Выбор инструмента моделирования определяется целью моделирования и формой представления информации об изучаемом объекте при его исследовании. В данной работе в качестве основного средства реализации информационных моделей на компьютере выступают системы программирования. Перед теми, кто научился программировать, должна открыться масса интересных и полезных задач. Программирование – это только инструмент для решения жизненных задач.
Глава 1. Основные понятия содержательной линии «Моделирование и формализация»
1. Понятие модели
Построение и использование моделей – мощное орудие познания. Реальные объекты и процессы бывают столь многогранны и сложны, что лучшим способом их изучения является построение моделей, отражающих лишь интересующие свойства этих объектов и поэтому более простых, чем эти объекты. Модели позволяют в наглядной форме представить объекты и процессы, недоступные для непосредственного восприятия (очень большие или очень маленькие объекты, очень быстрые или очень медленные процессы; такие, что исследование объекта или процесса опасно для окружающих или для исследуемого объекта). Поэтому для получения нужной информации об объектах-оригиналах проводят исследования на созданных моделях. При создании моделей нельзя учесть все свойства оригинала, какие-то свойства оказываются наиболее важными, а какими-то надо пренебречь. При этом появляется модель объекта (modulus – образ, способ, мера, от латинского modus).
Модель – это мысленно представимая или материально реализованная система, некоторый объект-заменитель, который в определенных условиях может заменять объект-оригинал, воспроизводя интересующие нас свойства и характеристики оригинала.
Примеры моделей: манекен – модель человеческого тела; модели самолетов, кораблей, автомобилей; таблица Менделеева; расписание занятий; уравнение зависимости перемещения тела при равномерном прямолинейном движении от скорости и времени движения.
У модели имеются существенные преимущества – наглядность, обозримость, доступность при исследовании. Модель замещает в процессе изучения, принятия решения оригинал, сохраняя те его черты, которые существенны для целей исследования. Изучение модели, объекта-заменителя, дает новую информацию об объекте-оригинале. Знания об окружающем мире меняют модели. Примером смены одних моделей другими, более адекватными, является история моделей Солнечной системы.
2. Классификация моделей
Рассматривая примеры моделей, ответим на следующие вопросы:
1. В какой форме представлена модель?
2. Что является оригиналом для данной модели?
3. Какова цель создания данной модели?
4. Какие свойства оригинала сохранены в модели?
Замечаем, что все приведенные модели можно разделить на два класса: натурные и информационные модели.
Примеры натурных моделей: глобус – модель планеты Земля; модели атомного строения вещества в химии; муляжи в анатомии; модели самолетов, кораблей, автомобилей. Общая черта, присущая приведенным моделям, состоит в том, что они копируют исходный объект, сохраняя внешний вид, структуру или поведение оригинала. Такие модели называют натурными.
В предмете «Информатика и ИКТ» рассматриваются другие модели – информационные.
Информационная модель – это модель, представляющая исследуемый объект или процесс набором данных и связей между ними, отражающими необходимую информацию об оригинале. В информационной модели отражаются знания человека об объекте моделирования. Пример информационной модели: представим себе, что нам подробно описали внешность человека, которого мы не видели, а затем по описанию мы узнали этого человека. Стало быть, в нашем сознании сложился некоторый образ человека, то есть создалась информационная модель. Большинство знаний, которые получает человек, носят характер информационных моделей. Решая жизненные задачи по физике, химии, экономике мы составляем уравнения, неравенства, системы уравнений и неравенств, в которых выражены интересующие нас связи между выделенными данными – мы составляем информационную модель. В дальнейшем будет приведено множество примеров информационных моделей.
Разные предметные области предлагают свою классификацию информационных моделей. Мы рассмотрим классификацию моделей, представленную на схеме (рис. 1).
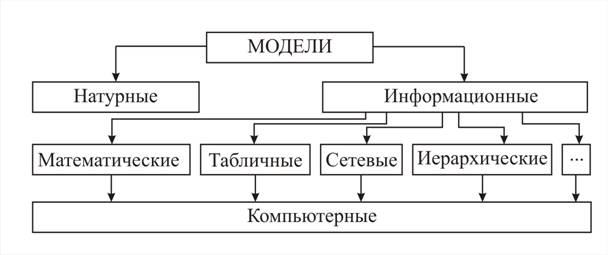
Рис. 1
По организации структуры данных и по форме представления этой структуры информационные модели можно классифицировать так:
1. Табличные информационные модели [15, 16].
2. Иерархические информационные модели [15, 16].
3. С етевые информационные модели [15, 16].
4. Математические модели – это информационные модели, в которых параметры и зависимость между ними выражены в математической форме.
5. Компьютерные модели – это модели, составленные в расчете на исполнителя, имитированного на компьютере. Исходные данные, результаты и связи между ними в компьютерной модели представлены в виде, «понятном» компьютерному исполнителю. Компьютерная модель – это информационная модель плюс алгоритм для реализации этой модели. Примеры исполнителей, имитированных на компьютере: Ершол-система, Delphi-система и др.
6. Аналоговые модели – это модели, в которых исследуемое явление изучается по аналогичному процессу, имеющему иную физическую природу, но которое описывается такими же математическими соотношениями. Например, колебания груза на пружине аналогично колебаниям тока в электрическом контуре, поэтому для изучения колебаний груза можно изучать колебание тока.
Математические модели можно разделить на следующие виды:
· Детерминированная модель (причинно-следственная модель) – это модель, параметры в которой, по крайней мере теоретически, поддаются точному измерению и управлению. Это аналитически представимая закономерность в объекте или процессе, при которой для любой комбинации значений параметров на входе будет получен единственный результат на выходе.
· Стохастическая модель – это математическая модель задачи, в которой параметры и связи между ними представляют собой случайные величины или случайные функции, законы распределения которых и другие статистические характеристики известны, а неопределенные факторы отсутствуют. Величина на выходе такой модели может быть представлена только в виде математического ожидания. Например, модель задачи массового обслуживания.
· Математическая модель с неопределенными условиями –модель, получаемая, когда параметры и связи не могут быть описаны статистическими методами. Методами обоснования решения в условиях неопределенности занимаются математическая теория игр и теория статистических решений.
3. Цели моделирования
1. Понимание объекта-оригинала. Модель нужна для того, чтобы узнать, как устроен конкретный объект, какова его структура, основные свойства объекта, законы развития и его взаимодействия с окружающим миром.
2. Управление объектом-оригиналом. Модель нужна для того, чтобы научиться управлять объектом, процессом, явлением и определить наилучшие способы управления при заданных целях и критериях.
3. Прогнозирование поведения объекта-оригинала. Модель нужна для того, чтобы прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект. Найти ответы на вопросы: «Что будет через какое-то время?» или «Что будет, если...?».
4. Границы адекватности модели
Если построенная модель дает удовлетворительные результаты при решении данной задачи, то говорят, что модель адекватна рассматриваемому объекту, процессу.
Модель не эквивалентна исходному объекту или процессу, а поэтому модель имеет ограниченную область адекватности. За пределами этой области она перестает удовлетворительно отражать свойства моделируемого объекта. Поэтому применять модель для решения той или иной жизненной задачи допустимо только тогда, когда мы убедились, что не вышли за границу области адекватности. Адекватность модели определяется ее согласованностью с практикой и общетеоретическими положениями.
В примерах данного пособия адекватность модели определяется либо сравнением результатов, полученных при исследовании модели, с результатами экспериментов с использованием других теоретически точных методов решения данной задачи, либо анализом частных решений поставленной задачи.
5. Основные понятия системологии
Понятие «система» часто употребляется как в науке, так и в повседневной жизни. Примеры: Солнечная система, периодическая система химических элементов, система образования, система транспорта, файловая система, операционная система и многие другие.
Объект – материальный объект, явление природы, процесс – это некоторая часть окружающей нас действительности, рассматриваемая как единое целое.
Под системой будем понимать сложный объект, состоящий из множества взаимосвязанных частей и существующий как единое целое. Всякая система имеет определенное назначение, функции и цель. В информатике понятие «система» употребляется достаточно часто. Например, совокупность взаимосвязанных данных, предназначенных для обработки на компьютере – система данных.
Важной характеристикой всякой системы является ее структура. Структура – это внутренняя организация системы, определенный порядок объединения элементов, составляющих систему.
Основным методическим принципом информационного моделирования считается системный подход, согласно которому всякий объект моделирования рассматривается как система. Из всего множества элементов, свойств и связей выделяются лишь те, которые будут существенными для целей моделирования.
Задача системного анализа, который проводит исследователь, – учесть системные связи всякого объекта изучения для того, чтобы в дальнейшем отразить их в информационной модели. Сама информационная модель представляет собой некоторую систему данных и отношений между ними. Эти данные и отношения могут быть представлены в разной форме: графической, математической, табличной и др. Составленная информационная модель далее реализуется на компьютере: составляются алгоритм и программа для проведения вычислительного эксперимента.
Схема перехода от реального объекта к компьютерной модели представлена на рис. 2.
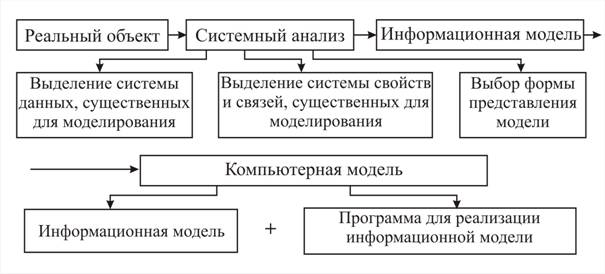
Рис. 2
Приведем классический пример системного подхода к составлению информационных моделей. Гуляя по городу Кенигсбергу (Калининграду), великий математик Леонард Эйлер (1707 – 1783 гг.) решал следующую задачу: как выбрать маршрут, чтобы побывать на всех берегах и островах реки Преголь, пройдя через каждый мост ровно один раз. План мостов в городе Кенигсберге:

Решение
Для решения задачи Эйлер использовал системно-информационный подход к анализу окружающей действительности. Объектом исследования являлась часть местности. Проведя системный анализ объекта моделирования, Эйлер выделил интересующие его элементы системы, установил между ними связь. Элементы системы – берега и острова, связь между ними – мосты, соединяющие данные элементы. Для простоты решения задачи он изобразил острова и оба берега точками, а мосты – отрезками линий (рис. 3). Эйлер построил информационную модель в виде графа.
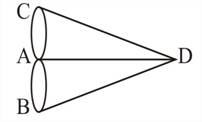
|
| Рис. 3 |
Решение задачи стало теперь почти очевидным. Чтобы удовлетворить требования задачи, нужно иметь возможность прийти в какую-либо точку по одному отрезку, а выйти из нее – по другому. Это не относится к начальной и конечной точкам, следовательно, из каждой точки, кроме может быть двух, должно выходить четное количество отрезков-рёбер. Для полученного рисунка сформулированное требование не выполняется. Значит, по мостам нельзя пройти, соблюдая условие задачи.
6. Этапы решения задач с использованием компьютера
Под процессом решения задачи с использованием компьютера надо понимать совместную деятельность человека и компьютера. На долю человека приходятся этапы, связанные с творческой деятельностью: постановка задачи, составление информационной модели, разработка алгоритма решения поставленной задачи, составление компьютерной модели, анализ результатов, а на долю компьютера – этапы обработки информации в соответствии с разработанным алгоритмом (рис. 4).
Этапы решения задач
1. Постановка задачи. Ставит задачу человек, который хорошо разбирается в предметной области задачи. На этом этапе происходит выбор объекта моделирования, определяется цель решения задачи, выполняются сбор информации об объекте моделирования, формулировка условия задачи, описание каждого исходного данного, определение формы выдачи результатов и предлагается общий подход к решению поставленной задачи.
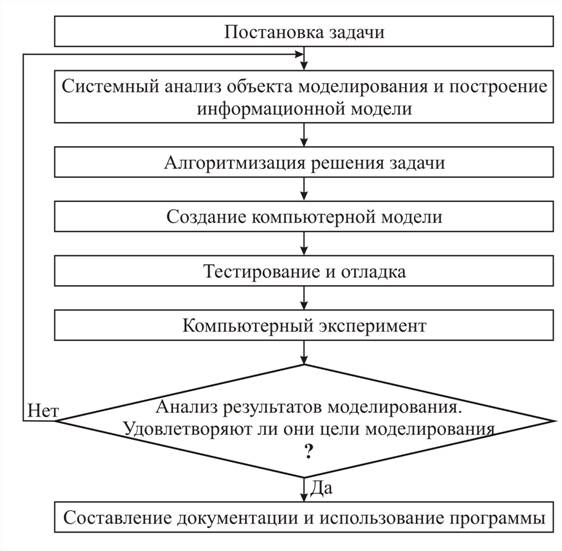
Рис. 4
2. Системный анализ объекта моделирования и построение информационной модели. Здесь происходят формализация задачи, анализ существующих аналогов изучаемого процесса, определение структур данных и типов связей между ними, выбор технических и программных средств. И в соответствии с выбранными средствами разрабатывается информационная модель, изучаемый объект или процесс заменяется информацией о нём в выбранной форме.
3. Алгоритмизация решения задачи – это выбор компьютерного исполнителя, метода проектирования алгоритма, формы записи алгоритма и проектирование алгоритма. Чаще всего алгоритм решения поставленной задачи на этом этапе описывается словесно или с использованием блок-схем.
4. Создание компьютерной модели – это описание решения задачи в виде программы для выбранного исполнителя, реализация алгоритма на компьютере.
5. Тестирование и отладка – синтаксическая отладка, отладка логической структуры, тестовые расчеты и анализ результатов тестирования, совершенствование программы.
6. Компьютерный эксперимент. Составляется план эксперимента и проводится сам эксперимент.
7. Анализ результатов моделирования. Проверяется адекватность модели и, если возможно, выделяются границы адекватности. Результаты проведённого эксперимента могут соответствовать или не соответствовать цели моделирования. Если результат эксперимента соответствует цели моделирования, то нужно перейти на шаг 8, иначе необходимо уточнить компьютерную модель с повторным выполнением шагов 2 – 7.
8. Доработка программы для решения конкретных задач, составление документации к компьютерной модели.
Следует заметить, что приведенная последовательность действий ориентирована на решение задач любой сложности. Для простейших задач некоторые этапы, возможно, не понадобятся. Для более сложных задач некоторые этапы могут существенно усложниться.
7. Пример решения задачи, в которой происходит развитие информационной модели
Рассмотрим пример решения задачи, в которой происходит развитие информационной модели вследствие её уточнения, так как результат эксперимента с первоначальной компьютерной моделью не соответствует цели моделирования, противоречит практике.
Задача. Два завода железобетонных изделий снабжаются цементом из двух складов. В сутки первому заводу необходимо 50 т цемента, второму – 90 т. С первого склада можно вывезти в сутки 60 т, со второго – 80 т цемента. Стоимость доставки тонны цемента из первого склада на первый завод составляет 1,4 тыс. руб., на второй – 2 тыс. руб. Стоимость доставки тонны цемента со второго склада на первый завод – 1,2 тыс. руб., на второй завод – 1,6 тыс. руб. Как распределить поставки, чтобы общая сумма расходов на перевозку была минимальной (табл. 1).
Таблица 1
| Склад | 1-й завод | 2-й завод | Доставка цемента |
| Первый | х 1 1400 руб. | х 2 2000 руб. | 60 т |
| Второй | х 3 1200 руб. | х 4 1600 руб. | 80 т |
| 50 т | 90 т | 140 т |
1-й этап. Постановка задачи. Поставим вопрос, какие факторы могут повлиять на организацию перевозок цемента со складов на заводы? Их много: болезнь водителей, выход из строя автомобилей, трудности с бензином и т.д. Эти факторы мы учитывать не будем. Предположим, что на автобазе есть резервы автомобилей, хорошо поставлено медицинское обслуживание, нет трудностей с горюче-смазочными материалами и т.д. Нас интересует только, как распределить цемент между заводами.
2-й этап. Системный анализ объекта моделирования и построение информационной модели. Выделим из условия задачи необходимую информацию и формализуем её. Введем обозначения: х 1 т – количество цемента, вывозимого с первого склада на первый завод; х 2 т – количество цемента, вывозимого с первого склада на второй завод; х 3 т – количество цемента, вывозимого со второго склада на первый завод; х 4 т – количество цемента, вывозимого со второго склада на второй завод. Так как в сутки потребность первого завода в цементе составляет 50 т, то должно выполнятся равенство х 1 + х 3 = 50.
По аналогии: 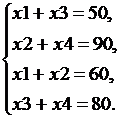 (1)
(1)
Эти равенства должны выполняться одновременно. По условию стоимость перевозки цемента в сутки на первый и второй заводы равна
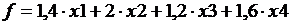 .
.
Из бесконечного множества решений системы (1) необходимо найти значения х 1, х 2, х 3, х 4, при которых линейная функция f принимает наименьшее неотрицательное значение.
3-й этап. Алгоритмизация решения задачи. Выберем исполнителя – Basic-систему. В системе ограничений все переменные выразим через х 1: 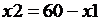 ;
; 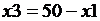 ;
; 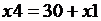 , подставим в функцию f выражения переменных и получим более простой вид функции f
, подставим в функцию f выражения переменных и получим более простой вид функции f
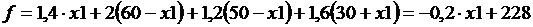 .
.
Мы уже говорили, что расходы на перевозку измеряются неотрицательной величиной, т. е. 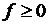 . Следовательно, минимальное значение f равно нулю.
. Следовательно, минимальное значение f равно нулю.
Алгоритм решения задачи:
1. Найти х 1 из уравнения: 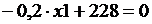 ;
;
2. Найти х 3 из уравнения: 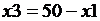 ;
;
3. Найти х 2 из уравнения: 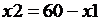 ;
;
4. Найти х 4 из уравнения: 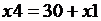 .
.
4-й этап. Создание компьютерной модели.
rem программа перевозки
dim x1 as single, x2 as single, x3 as single, x4 as single
let х1 = 228 / 0.2: let х2 = 60 – х1
let х3 = 50 – х1: let х4 = 30 + х1
print “X1 =”; х1; “X2 =”; х2; “X3 =”; х3; “X4 =”; х4
end
6-7-й этапы. Вычислительный эксперимент и анализ результатов эксперимента. В результате работы программы получили
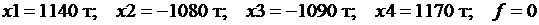 .
.
Можно сделать вывод, что результаты неправильные, они противоречат требованиям, поставленным в условии задачи (получили, что для обеспечения нормальной работы заводов, цемент с заводов надо вывозить). Модель неадекватна изучаемому процессу. Следовательно, при составлении информационной модели не были учтены важные факторы для решения поставленной задачи. Вернемся на шаг 2.
2-й этап. Уточним информационную модель, введя добавочные ограничения  .
.
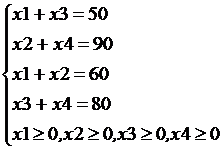
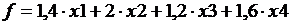
3-й этап. Алгоритмизация решения задачи. Для составления алгоритма исследуем математическую модель.
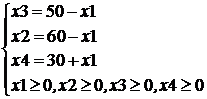 Þ
Þ 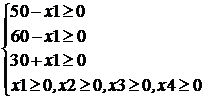 Þ
Þ 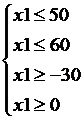 Þ Þ
Þ Þ 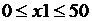 .
.
Легко видеть, что, если х 1 возрастает к 50, то функция 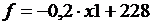 убывает, следовательно, наименьшее значение эта функция принимает при х 1 = 50.
убывает, следовательно, наименьшее значение эта функция принимает при х 1 = 50.
6-7-й этапы. Составление компьютерной модели, вычислительный эксперимент.
rem программа перевозки
dim x1 as single, x2 as single, x3 as single, x4 as single
let х1 = 50: let х2 = 60 – х1
let х3 = 50 – х1: let х4 = 30 + х1
print “X1 =”; х1; “X2 =”; х2; “X3 =”; х3; “X4 =”; х4; “ f = ”;-0.2*x1+228
end
Результаты эксперимента: 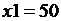 ;
; 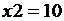 ;
; 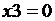 ;
; 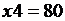 .
.
Наименьшее значение функции  . Решение удовлетворяет поставленным целям. Получили, что минимальные затраты на перевозку будут составлять 218 тыс. руб., если с первого склада ежедневно вывозить на первый завод 50 т цемента, на второй – 10 т, а со второго склада вывозить цемент только на второй завод 80 т ежедневно.
. Решение удовлетворяет поставленным целям. Получили, что минимальные затраты на перевозку будут составлять 218 тыс. руб., если с первого склада ежедневно вывозить на первый завод 50 т цемента, на второй – 10 т, а со второго склада вывозить цемент только на второй завод 80 т ежедневно.
9. Некоторые методы составления информационных моделей
9.1. Составление информационных моделей с использованием метода дискретизации
Пусть на отрезке [ а, b ] задана непрерывная функция 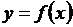 , и отрезок [ а, b ] разбит на n элементарных отрезков точками
, и отрезок [ а, b ] разбит на n элементарных отрезков точками 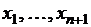 .
.
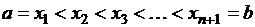 .
.
На каждом из полученных отрезков 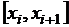 ,
, 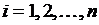 заменим непрерывную функцию
заменим непрерывную функцию 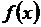 одним значением этой функции, получим последовательность
одним значением этой функции, получим последовательность 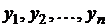 (рис. 5).. Либо на каждом из этих числовых интервалов непрерывную функцию
(рис. 5).. Либо на каждом из этих числовых интервалов непрерывную функцию 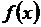 заменим одним значением функции, приближающей данную с определённой точностью, например, функции z. Получим последовательность
заменим одним значением функции, приближающей данную с определённой точностью, например, функции z. Получим последовательность 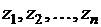 .
.
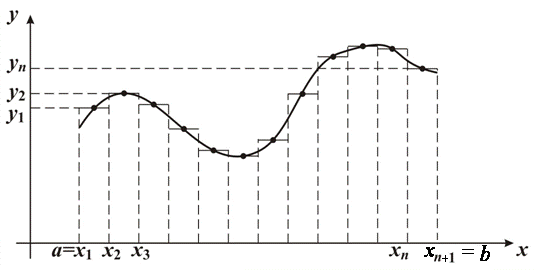
Рис. 5
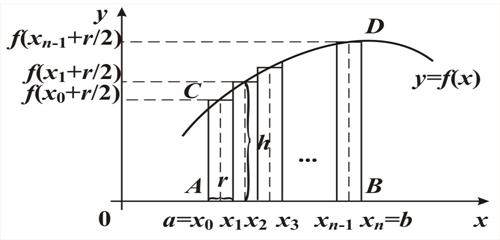
f(x0 +r/2),f(x1 + r/2), …,f(xn-1 +r/2)
Заменили непрерывную функцию у =  на отрезке [ a, b ] области определения функции конечной последовательностью дискретных значений этой функции: f(x0 +r/2),f(x1 + r/2), …,f(xn-1 +r/2). Такой процесс называется дискретизацией функции у = f(x) на отрезке [ a, b ] области определения функции.
на отрезке [ a, b ] области определения функции конечной последовательностью дискретных значений этой функции: f(x0 +r/2),f(x1 + r/2), …,f(xn-1 +r/2). Такой процесс называется дискретизацией функции у = f(x) на отрезке [ a, b ] области определения функции.
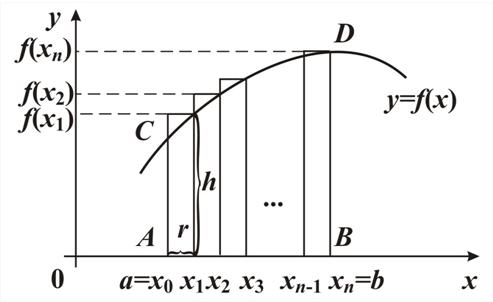
Через y1,...,уn обозначим значения функции у=f (х) в точках деления х1,..., хn, a=x0, b=x n
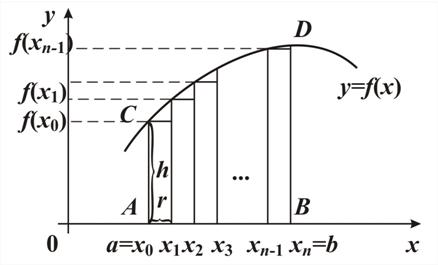
Через у0, y1,...,уn-1 обозначим значения функции у=f (х) в точках деления х0, х1,..., хn-1, a=x0, b=x n

Заменили непрерывную функцию у = 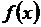 на отрезке [ a, b ] области определения функции конечной последовательностью дискретных значений функции, приближающей данную функцию с определенной точностью: у 0, y 1,...,уn-1 ИЛИ
на отрезке [ a, b ] области определения функции конечной последовательностью дискретных значений функции, приближающей данную функцию с определенной точностью: у 0, y 1,...,уn-1 ИЛИ 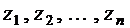 . Такой процесс называется дискретизацией функции у = f(x) на отрезке [ a, b ] области определения функ
. Такой процесс называется дискретизацией функции у = f(x) на отрезке [ a, b ] области определения функ 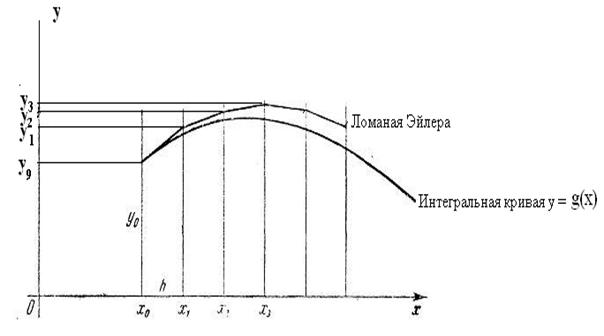 ции.
ции.
Процесс замены непрерывной функции 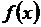 на отрезке [ a, b ] области определения функции конечной последовательностью дискретных значений этой функции или функции, приближающей данную функцию с определенной точностью, называется дискретизацией.
на отрезке [ a, b ] области определения функции конечной последовательностью дискретных значений этой функции или функции, приближающей данную функцию с определенной точностью, называется дискретизацией.
Рассмотрим некоторые примеры применения метода дискретизации при составлении информационных моделей для решения жизненных задач.
Пример 1. 1-й этап. Постановка задачи. Тело движется прямолинейно с ускорением а м/c2 и скоростью v м/c. Определите, какой путь пройдет тело за ts секунд [14].
Date: 2015-07-17; view: 844; Нарушение авторских прав