
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Требования к уровню подготовки учащихся 2 page
|
|
Поставим цель – получить информационную модель.
2-й этап. Анализ объекта моделирования и построение информационной модели. Проведём системный анализ задачи, определим исходные данные и результаты. Аргументы: начальная скорость v, ускорение а, время движения ts. Результат – путь S.
Построим приближённую информационную (математическую) модель равноускоренного прямолинейного движения. Применим метод дискретизации для нахождения значения пути, пройденного телом за время ts при равноускоренном прямолинейном движении. Интервал времени ts разобьём на очень большое количество равных малых промежутков. Отрезок [0, ts ] разделим на n равных отрезков длины 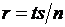 .
.

Сделаем некоторые предположения:
1-е предположение. Если интервал времени разбить на очень большое количество равных малых промежутков, то мы не сильно ошибёмся, предполагая, что скорость тела на каждом из этих промежутков времени постоянна (то есть на каждом из этих промежутков движение прямолинейное равномерное) и меняется мгновенно в конце каждого промежутка.
2-е предположение. При неограниченном увеличении числа отрезков разбиения мы получим величину перемещения с любой точностью.
Замечание. Правильность и полнота предположений, на которых основана информационная модель, должны быть проверены на практике или строго доказаны.
Будем находить путь на каждом промежутке, считая, что скорость тела на этих промежутках постоянна. Рассмотрим один из этих отрезков. Выберем на нём какой-нибудь момент времени 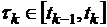 ,
,  , найдём соответствующее ему значение скорости
, найдём соответствующее ему значение скорости 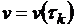 . Будем считать движение на этом отрезке равномерным со скоростью
. Будем считать движение на этом отрезке равномерным со скоростью 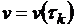 ,
, 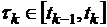 . Аналогичные действия проделаем для каждого временного отрезка. Заменим исследуемую функцию (путь при равноускоренном прямолинейном движении) на каждом из интервалов деления на приближающую функцию (путь при равномерном прямолинейном движении). Разным разбиениям отрезка
. Аналогичные действия проделаем для каждого временного отрезка. Заменим исследуемую функцию (путь при равноускоренном прямолинейном движении) на каждом из интервалов деления на приближающую функцию (путь при равномерном прямолинейном движении). Разным разбиениям отрезка 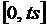 на n равных отрезков и разному выбору моментов
на n равных отрезков и разному выбору моментов 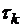 будут соответствовать разные значения пути, пройденного телом за ts секунд.
будут соответствовать разные значения пути, пройденного телом за ts секунд.
Ñ Пусть 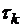 совпадает с левым концом выбранного отрезка, то есть считаем, что на протяжении одного временного промежутка скорость тела не изменяется и равна скорости в начале этого временного отрезка, а меняется мгновенно по истечении этого интервала времени (скорость увеличивается). Заменим плавно увеличивающийся путь, пройденный телом за время ts, на последовательность значений пути, пройденного со скоростью
совпадает с левым концом выбранного отрезка, то есть считаем, что на протяжении одного временного промежутка скорость тела не изменяется и равна скорости в начале этого временного отрезка, а меняется мгновенно по истечении этого интервала времени (скорость увеличивается). Заменим плавно увеличивающийся путь, пройденный телом за время ts, на последовательность значений пути, пройденного со скоростью 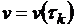 ,
, 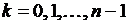 , на каждом из отдельных временных отрезков.
, на каждом из отдельных временных отрезков.
Составим математическое соотношение (информационную модель), связывающее аргументы и результат.
Отрезок 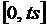 разделили на n равных отрезков длины
разделили на n равных отрезков длины 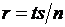 .
.
 |
Найдем путь за время движения ts 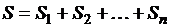 , где
, где 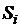 – длина пути на i- м промежутке времени,
– длина пути на i- м промежутке времени, 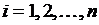 .
.
В силу первого предположения имеем: 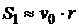 ,
, 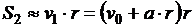 ,
, 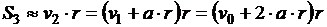 , …,
, …, 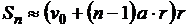 .
.
Тогда, 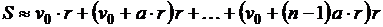 .
.
Вынесем r за скобки, для вычисления выражения в скобках воспользуемся формулой для вычисления суммы n членов арифметической прогрессии.
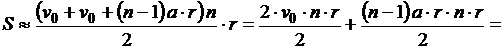
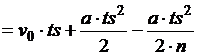 , (используем равенство
, (используем равенство 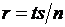 ), ts=r*n.
), ts=r*n.
Получим
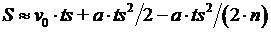 .
.
Обобщим эту формулу для произвольного t – времени движения тела
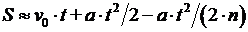 . (2)
. (2)
При неограниченном увеличении числа отрезков разбиения мы получим величину перемещения с любой точностью.
Формула (2) и является математическим соотношением для нахождения приближённого значения пути, которое пройдёт тело за время t (ts). Построение информационной (математической) модели закончено
Замечание. Предел выражения, стоящего в правой части равенства (2) (при 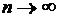 ), если он существует, есть определённый интеграл от функции
), если он существует, есть определённый интеграл от функции 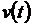 на отрезке
на отрезке 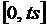 и обозначается:
и обозначается:
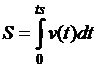 . (3)
. (3)
Имеем,  , или
, или
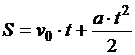 .
.
3-4-й этапы. Алгоритмизация решения задачи и создание компьютерной модели. Выберем исполнителя – Ершол-систему. Компьютерная модель имеет вид:
алг путь (аргвещ a, v0, t, аргцел n, резвещ s)
дано | a –ускорение, v0-начальная скорость
| t – время в пути, n- число разбиений
надо | напечатано S –значение пройденного пути за время t
нач
s: = v0 * t + a * t * t / 2 – a * t * t / (2 * n)
кон
Проведите вычисления, изменяя исходные данные, оформите результаты в виде таблицы.
| v 0 | a | t | n | S |
6-й этап. Вычислительный эксперимент, проверка адекватности модели изучаемому процессу.
Мы знаем другую формулу нахождения пути, который пройдёт тело за время t, при прямолинейном равноускоренном движении:
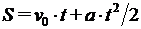 (4)
(4)
Выведенная формула (2) отличается от (4) последним слагаемым, которое показывает, с какой степенью точности построенная модель описывает равноускоренное движение.
6.1. Определим адекватность модели, проведя вычисления по построенной формуле (2) и по формуле (4),используя программу:
алг путь (аргвещ a, v0, t, аргцел n, резвещ s, s1, ds)
дано | a –ускорение, v0-начальная скорость
| t – время движения тела, n- число разбиений
надо | напечатано S –значение пути за время t по формуле (2)
| напечатано s1- значение пути за время t по формуле (4)
| напечатано ds – абсолютная величина разности s и s1
нач
s: = v0*t + a*t*t/2 – a*t*t/(2*n)
s1: = v0*t + a*t*t/2
ds: = abs (s1–s)
кон
С теоретической точки зрения, при увеличении n значение ds должно стремиться к 0. Но при вычислении с использованием компьютера происходит накопление ошибок округления, поэтому для каждого метода существует пороговое значение 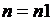 такое, что при
такое, что при 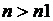 , ds перестает уменьшаться.
, ds перестает уменьшаться.
Проведите вычисления, изменяя исходные данные, оформите результаты в виде таблицы.
| v 0 | a | t | n | S | S1 | dS |
6.2. Вычислим путь, пройденный телом, с заданной точностью. Обычно точный результат решения задачи неизвестен. Как оценить точность полученного решения? Рассмотрим простейший прием, часто применяемый на практике. Проведем вычисление пути S по формуле (2) с заданным n – числом разбиений отрезка 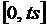 , затем вычислим путь S 1 с числом разбиений, равным
, затем вычислим путь S 1 с числом разбиений, равным 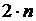 , и так далее. Вычислительный эксперимент показывает, что с увеличением числа разбиений соседние результаты
, и так далее. Вычислительный эксперимент показывает, что с увеличением числа разбиений соседние результаты 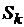 и
и 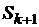 мало отличаются друг от друга. Будем считать, что, если
мало отличаются друг от друга. Будем считать, что, если 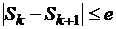 , то
, то 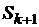 вычислено с точностью до е, где e – точность вычисления.
вычислено с точностью до е, где e – точность вычисления.
Опишем алгоритм и программу вычисления пути S по формуле (2) с заданной точностью е, используя рассмотренный прием.
алг путь1 (аргвещ a, v0, t, е, аргцел n, резвещ S1)
дано | a –ускорение, v0-начальная скорость
| е – точность вычислений
| t – время движения, n- число разбиений
надо | напечатано S1 –значение пути за время t,
| вычисленное по формуле (2) с точностью е
нач
S: = v0 * t + a * t * t / 2 – a * t * t / (2 * n)
n:=n * 2; S1:= v0 * t + a * t * t / 2 – a * t * t / (2 * n)
нцпока abs(S1–S) > e
S:= S1; n:=n * 2
S1:= v0 * t + a * t * t / 2 – a * t * t / (2 * n)
кц
кон
Проведя вычисления, получаем значения пути с различной точностью е.
Проведите вычисления, изменяя исходные данные, оформите результаты в виде таблицы.
| v 0 | a | t | n | e | S | S 1 |
| … | … | … | … | … | … |
Пример 2. 1-й этап. Постановка задачи. Тело падает с высоты h м, определите высоту тела над землёй через th секунд после начала падения. При решении задачи учтите сопротивление воздуха. Для выбранных начальных значений аргументов, проводя эксперимент, определите возможные границы th, задавайте при вычислительном эксперименте реальные значения th [10].
2-й этап. Анализ объекта моделирования и построение информационной модели. Определим исходные данные и результаты задачи. Аргументами являются: g – ускорение свободного падения, h 0 – начальная высота падения, v 0 – начальная скорость, th – время падения тела. Результат – высота тела над землёй через th секунд после начала падения. Мы не знаем точных формул, выражающих высоту тела над землёй с учётом сопротивления воздуха через th секунд после начала падения.
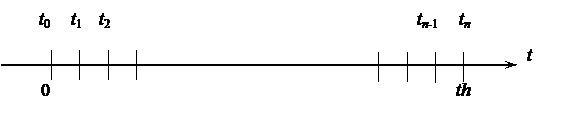 Экспериментально установлено, что сила сопротивления воздуха пропорциональна квадрату скорости, коэффициент пропорциональности зависит от формы тела. Пусть для некоторого момента времени t нам известны высота тела
Экспериментально установлено, что сила сопротивления воздуха пропорциональна квадрату скорости, коэффициент пропорциональности зависит от формы тела. Пусть для некоторого момента времени t нам известны высота тела 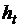 и скорость тела
и скорость тела 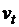 . Тогда ускорение можно вычислить по формуле
. Тогда ускорение можно вычислить по формуле 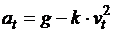 , где
, где 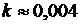 (для усредненного тела). Для составления информационной модели применим метод дискретизации непрерывных процессов. Разобьем время падения th на небольшие интервалы dt.
(для усредненного тела). Для составления информационной модели применим метод дискретизации непрерывных процессов. Разобьем время падения th на небольшие интервалы dt.
Будем считать, что на протяжении одного интервала параметры задачи не изменяются, а меняются мгновенно по истечении этого интервала (уменьшается ускорение, увеличивается скорость падения тела, уменьшается высота расположения тела над землей). Заменим плавно уменьшающуюся высоту тела над землёй на последовательность значений высот в моменты времени
 ,
, 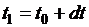 ,
, 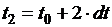 ,…,
,…, 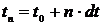 . Подсчитаем высоту тела над землёй и скорость тела через промежуток времени dt:
. Подсчитаем высоту тела над землёй и скорость тела через промежуток времени dt: 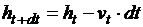 – считаем, что движение на этом промежутке времени равномерное;
– считаем, что движение на этом промежутке времени равномерное; 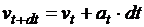 – считаем, что ускорение a на этом промежутке не меняется.
– считаем, что ускорение a на этом промежутке не меняется.
Информационная модель данного процесса имеет вид:
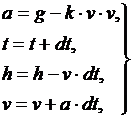 (11)
(11)
где t – время, прошедшее с начала падения, h – расстояние тела до поверхности земли в момент времени t, v – скорость тела в момент времени t, a – ускорение падения в момент времени t, dt – интервал времени, в течение которого не изменяется ускорение и скорость.
3-4-й этапы. Алгоритмизация решения задачи, создание компьютерной модели. Выберем исполнителя Pascal-систему. Зададим начальные значения аргументов: 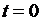 ,
, 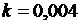 ,
, 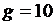 . Введем начальные значения v 0 и h 0. Значения ускорения, высоты, скорости в следующий момент времени
. Введем начальные значения v 0 и h 0. Значения ускорения, высоты, скорости в следующий момент времени 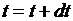 будем вычислять по рекуррентным соотношениям (11). Определим, на какой высоте над землёй будет находиться тело через th секунд после начала падения. Вычисления проводим пока
будем вычислять по рекуррентным соотношениям (11). Определим, на какой высоте над землёй будет находиться тело через th секунд после начала падения. Вычисления проводим пока 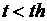 . Программа на языке Pascal имеет вид:
. Программа на языке Pascal имеет вид:
Program height;
var v0, h0,v, h, t, dt, a, th: real; const g = 10; k = 0.004;
begin
t:=0; write(‘ введите v0’); readln(v0); v:=v0; write(‘ введите th’); readln(th); write (‘введите h0, dt’); readln (h0, dt); h:=h0;
while t<th do
begin
t: = t + dt; a: = g – k * v * v; h: = h – v * dt; v: = v + a * dt;
write (‘t = ‘, t, ‘h = ‘, h, ’v= ‘, v);
end;
end.
Проведите вычисления, изменяя исходные данные, оформите результаты в виде таблицы.
| th | dt | v0 | h0 | t | v | h |
6-й этап. Вычислительный эксперимент, проверка адекватности модели изучаемому процессу.
6.1. Проверим адекватность модели исследуемому процессу. Если 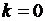 , то высота тела над землёй через th секунд после начала падения с учетом сопротивления будет соответствовать высоте тела над землёй через th секунд после начала падения в вакууме. Высоту h и скорость тела v в любой момент времени падения без учета сопротивления воздуха можно вычислить точно по формулам
, то высота тела над землёй через th секунд после начала падения с учетом сопротивления будет соответствовать высоте тела над землёй через th секунд после начала падения в вакууме. Высоту h и скорость тела v в любой момент времени падения без учета сопротивления воздуха можно вычислить точно по формулам
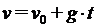 ;
; 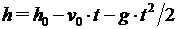 (12)
(12)
Определим высоту тела над землёй, используя точные формулы (12) и формулы (11), где 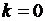 , и сравним полученные результаты. Программа для эксперимента имеет вид:
, и сравним полученные результаты. Программа для эксперимента имеет вид:
program height1;
var h1, v0, h0, v1, h,v, t, dt, a, th: real;
const g = 10; k=0;
begin
t:=0; write(‘ введите v0’); readln (v0); v:=v0; write(‘ введите th’); readln(th); write (‘введите h0, dt’); readln (h0, dt); h:=h0; v1:=v0;h1:=h0;
writeln (‘ t = ‘, t, ‘ h = ‘, h, ‘ v = ‘, v, ‘ v1 = ‘, v1, ‘ h1 = ‘, h1);
while t<th do
begin
a:= g – k*v*v; t:= t + dt; h:= h – v*dt; v:= v + a*dt;
v1:= v0 + g*t; h1:= h0 – v0*t – g*t*t/2;
writeln (‘ t = ‘, t, ‘ h = ‘, h, ‘ v = ‘, v, ‘ v1 = ‘, v1, ‘ h1 = ‘, h1);
end;
end.
Проведя вычислительный эксперимент с фиксированной начальной скоростью и начальной высотой и различными значениями dt, можно сделать вывод, что с уменьшением dt приближенное решение приближается к точному решению.
Проведите вычисления, изменяя исходные данные, оформите результаты в виде таблицы.
| th | dt | v0 | h0 | t | v | v1 | h | h1 |
6.2. Вычислим с заданной точностью высоту тела над землёй через th cекунд после начала падения.
Для получения результата с заданной точностью e применим приём, рассмотренный в примере 1. Используя модель, найдем высоту 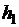 над землей через th секунд после падения при выбранном dt; возьмем
над землей через th секунд после падения при выбранном dt; возьмем  и вычислим
и вычислим 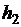 , высоту тела над землей через th секунд после падения. Затем снова уменьшим dt в два раза, вычислим
, высоту тела над землей через th секунд после падения. Затем снова уменьшим dt в два раза, вычислим 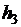 и так далее. Вычислительный эксперимент показывает, что с увеличением числа разбиений временного отрезка th соседние результаты
и так далее. Вычислительный эксперимент показывает, что с увеличением числа разбиений временного отрезка th соседние результаты 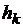 и
и 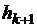 , мало отличаются друг от друга. Будем считать, что если
, мало отличаются друг от друга. Будем считать, что если 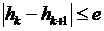 , то
, то 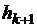 есть искомая высота тела над землей через th секунд после начала падения, вычисленная с заданной точностью e.
есть искомая высота тела над землей через th секунд после начала падения, вычисленная с заданной точностью e.
program fall;
const k = 0.004;
g = 10;
var h1, h2, h0, h, v0, v, t, dt, a, e, th: real;
procedure height (dt: real; var h: real);
begin
v:= v0; h:= h0; t:=0;
while t < th do
begin
a:= g – k*v*v; t:= t + dt; h:= h – v*dt; v:= v + a*dt;
end;
end;
begin
write (‘Введите h0, v0, dt, e, th’); readln (h0, v0, dt, e, th);
height (dt, h); h1:= h; dt:= dt/2; height (dt, h); h2:= h;
while abs (h2 – h1) > e do
begin
h1:= h2; dt:= dt/2; height (dt, h); h2:= h;
end;
write (‘ h = ‘, h2, ‘ h1 = ‘, h1, ‘ e =’, e, ‘ th = ‘, th);
end.
Проведя вычисления, получаем значения высоты тела над землёй с различной точностью е.
Проведите вычисления, изменяя исходные данные, оформите результаты в виде таблицы.
| h 0 | v 0 | th | dt | e | h 1 | h 2 |
9.2. Метод Монте-Карло
9.2.1. Введение
Метод Монте-Карло – метод решения задач при помощи моделирования случайных величин. Датой рождения метода Монте-Карло принято считать 1949 год, когда появилась статья под названием «The Monte Carlo method». Создателями этого метода считают американских математиков Дж. Неймана и С. Улама. В Советском Союзе первые статьи о методе Монте-Карло были опубликованы в 1955-1956 годах. Теоретическая основа метода была известна уже давно, некоторые задачи статистики рассчитывались иногда с помощью специальных выборок, то есть фактически методом Монте-Карло. Однако до появления электронно-вычислительных машин этот метод не мог найти сколько-нибудь широкого применения, ибо моделировать случайные величины вручную – очень трудоёмкая работа. Возникновение метода Монте-Карло как универсального метода моделирования стало возможным только благодаря появлению электронно-вычислительных машин. Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своими игорными домами.
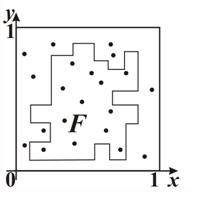
Как можно использователь метод Монте-Карло при составлении компьютерных моделей? Рассмотрим использование метода Монте-Карло при составлении компьютерных моделей на примере вычисления площадей плоских фигур. Предположим, что нам нужно вычислить площадь S плоской фигуры. Это может быть совсем произвольная фигура с криволинейной границей, заданная графически или аналитически, связная или состоящая из нескольких кусков. Пусть это будет фигура F, изображенная на рис. 12, и предположим, что она вся расположена внутри единичного квадрата, площадь которого 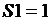 .
.
|
| Рис. 12 |
Будем многократно бросать в квадрат случайные точки (песчинки). Обозначим через n количество точек, брошенных в квадрат, через m – количество точек, попавших при этом внутрь фигуры F. Геометрически очевидно, что отношение площадей 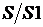 приближенно равно отношению
приближенно равно отношению 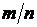 . Отсюда
. Отсюда 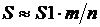 . Чем больше будет n, тем точнее вычисленная площадь.
. Чем больше будет n, тем точнее вычисленная площадь.
На практике для вычисления площадей плоских фигур метод Монте-Карло не используют, для этого есть другие методы, хотя и более сложные, но зато обеспечивающие большую точность. Однако указанный в нашем примере подход к составлению информационных моделей, метод Монте-Карло, позволяет просто вычислять «многомерный объем» тела в многомерном пространстве. И в этом случае метод Монте-Карло часто оказывается единственным методом, дающим возможность решить задачу. Включение задач на вычисление площадей плоских фигур с использованием метода Монте-Карло в школьный предмет «Информатика и ИКТ» позволяет понять суть этого метода при моделировании. Метод Монте-Карло вычисления площадей будет справедлив только тогда, когда случайные точки будут не «просто случайными», а еще и «равномерно разбросанными» по всей плоскости.
Выделим задачи, которые решаются методом Монте-Карло. Во-первых, метод Монте-Карло позволяет моделировать любой процесс, на протекание которого влияют случайные факторы. Во-вторых, для многих математических задач, не связанных с какими-либо случайностями, можно искусственно придумать вероятностную модель, позволяющую решать эти задачи.
Две особенности метода Монте-Карло.
1. Простая структура вычислительного алгоритма. Как правило, составляется программа для осуществления одного случайного испытания (в примере надо выбрать случайную точку в квадрате и проверить, принадлежит ли она F), затем это испытание многократно повторяется, причем каждый опыт не зависит от всех остальных. Иногда метод Монте-Карло называют методом статистических испытаний.
2. Ошибки вычислений, как правило, пропорциональны 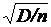 , где D – некоторая постоянная, а n – число испытаний. Из этой формулы видно, что для того чтобы уменьшить ошибку в 10 раз (иначе говоря, чтобы получить в ответе еще один верный десятичный знак), нужно увеличить n (то есть объем работы) в 100 раз. Обычно говорят, что метод Монте-Карло особенно эффективен при решении тех задач, в которых результат нужен с небольшой точностью (5-10 %). Во многих задачах удается значительно увеличить точность, выбрав способ расчета, которому соответствует значительно меньшее значение D.
, где D – некоторая постоянная, а n – число испытаний. Из этой формулы видно, что для того чтобы уменьшить ошибку в 10 раз (иначе говоря, чтобы получить в ответе еще один верный десятичный знак), нужно увеличить n (то есть объем работы) в 100 раз. Обычно говорят, что метод Монте-Карло особенно эффективен при решении тех задач, в которых результат нужен с небольшой точностью (5-10 %). Во многих задачах удается значительно увеличить точность, выбрав способ расчета, которому соответствует значительно меньшее значение D.
9.2.2. Примеры решения задач с использованием метода
Монте-Карло
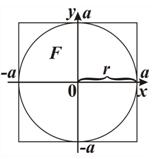
Пример 3. Рассмотрим в качестве примера информационную (математическую) и компьютерную модели для приближенного нахождения площади круга радиусом r, рис. 13.
1-й этап. Постановка задачи. Дан круг радиусом r, вычислите площадь круга. Результатом решения задачи является площадь S данного круга. Будем считать, что аналитическую формулу для вычисления площади круга мы не знаем.
2-й этап. Анализ объекта моделирования и построение информационной модели. Можно предложить разные модели для решения этой задачи. Например, можно использовать палетку: на фигуру накладывается клетчатая прозрачная бумага (палетка), и подсчитывается количество квадратиков, попавших в фигуру. В этой модели предполагается, что чем мельче клетки, тем точнее будет результат вычислений независимо от того, каким образом наложить палетку на фигуру. Можно придумать и «физическую» модель: скопировать фигуру из картона, аккуратно вырезать ее, взвесить и поделить на вес единичного квадрата из этого же картона. Однако по этим моделям трудно составить алгоритм и программу для расчетов на компьютере.
|
| Рис. 13 |
Построим информационную (математическую) модель. Для построения информационной модели используем подход, рассмотренный выше для нахождения площади фигуры F. Поместим фигуру F в квадрат наименьшего размера.
Будем многократно бросать в квадрат случайные точки. Введем следующее допущение. Пусть исходы испытания распределены равномерно. Это означает, что если разделить некоторую область S на конечное число равновеликих частей 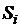 ,
,  , то можно считать, что вероятность попадания наудачу выбранной точки из области S в какую-либо часть
, то можно считать, что вероятность попадания наудачу выбранной точки из области S в какую-либо часть 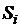 этой области пропорциональна мере этой части и не зависит от ее расположения и формы. Следовательно,
этой области пропорциональна мере этой части и не зависит от ее расположения и формы. Следовательно, 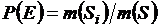 , где
, где 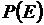 – вероятность того, что наудачу выбранная точка из области S окажется в области
– вероятность того, что наудачу выбранная точка из области S окажется в области 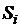 , a
, a 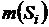 и
и 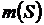 есть меры соответствующих областей, выраженных в единицах длины, площади или объема.
есть меры соответствующих областей, выраженных в единицах длины, площади или объема.
Исходными данными предложенной задачи являются r – радиус круга, количество точек n, которые случайным образом выбираются внутри квадрата. Число m – это количество точек, попавших внутрь круга, S – площадь круга. Результат и исходные данные связаны между собой соотношением 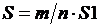 , где
, где 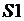 – площадь квадрата. К связям между исходными данными и результатом следует отнести и математические соотношения, позволяющие определить, попала ли выбранная точка в фигуру F.
– площадь квадрата. К связям между исходными данными и результатом следует отнести и математические соотношения, позволяющие определить, попала ли выбранная точка в фигуру F.
Date: 2015-07-17; view: 579; Нарушение авторских прав