
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Требования к уровню подготовки учащихся 3 page
|
|
Примем, а=r, где а – половина длины стороны квадрата, площадь 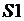 квадрата вычисляется по формуле
квадрата вычисляется по формуле 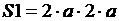 . Случайным образом выбираем точку, принадлежащую квадрату. Выбрать точку – значит задать ее координаты, то есть задать значения x и y.
. Случайным образом выбираем точку, принадлежащую квадрату. Выбрать точку – значит задать ее координаты, то есть задать значения x и y.
Информационная модель
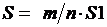 ,
, 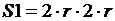 .
.
Точка принадлежит квадрату, если выполняются соотношения 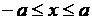 ,
, 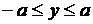 или
или 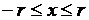 ,
, 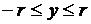 . Точка принадлежит кругу, если справедливо неравенство
. Точка принадлежит кругу, если справедливо неравенство 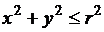 или
или 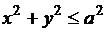 .
.
3-4-й этапы. Алгоритмизация решения задачи и создание компьютерной модели. Выберем исполнителя программы – Basic-систему. Запрограммируем создание последовательности случайных чисел и выбор случайных чисел из этой последовательности. Для создания последовательности случайных чисел используем процедуру randomize timer, для выбора «следующего» случайного числа из созданной последовательности случайных чисел используем функцию rnd, которая возвращает случайное число в диапазоне от 0 до 1.
Разработаем программу вычисления площади круга радиуса r=a.
randomize timer ′создание последовательности случайных чисел.
Let x = (a - (- a)) * rnd + (- a) ′выбор следующего случайного числа
'из диапазона от – а до а и присвоение этого значения переменной х.
Let y = (a - (- a)) * rnd + (- a) 'выбор следующего случайного числа
'из диапазона от – а до а и присвоение этого значения переменной y.
Пару случайных чисел x и y будем рассматривать как координаты точки, принадлежащей квадрату со стороной 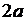 .
.
Совокупность команд, определяющих, принадлежит ли точка М(x,y) фигуре, площадь которой нужно найти, оформим в виде подпрограммы-функции Belong%.
Программа для вычисления площади круга радиуса r имеет вид:
DECLARE FUNCTION belong% (x AS DOUBLE, y AS DOUBLE, a AS DOUBLE)
' Метод Монте-Карло для вычисления площади фигуры F
DIM a AS DOUBLE, x AS DOUBLE, y AS DOUBLE, S AS DOUBLE
DIM S1 AS DOUBLE, n AS LONG, i AS LONG, m AS LONG, r AS DOUBLE
PRINT "Введите n - количество бросаемых точек";
INPUT n
PRINT "Введите r";
INPUT r: Let a=r: LET m= 0: RANDOMIZE TIMER
FOR i = 1 TO n
LET x = 2 * a * RND - a: LET y = 2 * a * RND - a
IF Belong% ((x), (y), (a)) = 1 THEN
LET m = m + 1
END IF
NEXT i
LET S1 = 2 * a * 2 * a: LET S = (m / n) * S1
PRINT "n= "; n; " s = "; S
END
FUNCTION Belong% (x AS DOUBLE, y AS DOUBLE, a AS DOUBLE)
LET belong% = 0
IF x * x + y * y <= a * а THEN
LET Belong% = 1
END IF
END FUNCTION
| Программа на языке Turbo Pascal | Программа на языке Ершол |
| program area; uses crt; var a,r,S,S1,x,y:real; m,n,i:longint; Function belong:boolean; begin belong:= false; IF x * x + y * y <= a * a THEN belong:= true; end; begin write ('Введите радиус круга r '); readln (r); write ('Введите количество бросаемых точек n '); readln (n); a:=r; m:=0; randomize; for i:=1 to n do begin x:= 2 * a * random - a; y:= 2 * a * random - a; if belong then m:= m + 1; end; S1:= 2 * a * 2 * a; S:= (m / n) * S1; writeln('n= ', n, ' s = ', S); end. | алг площадь круга (арг вещ r,арг цел n,рез вещ S) нач вещ S1,a,x,y, цел i,m a:=r; m:=0 нц для i от 1 до n x:= 2 * a * rnd(1) - a y:= 2 * a * rnd(1) - a; если Belong (x,y,a) то m:= m + 1 все кц S1:= 2 * a * 2 * a; S:= (m / n) * S1 вывод нс,S,нс кон алг лог Belong (арг вещ x,y,a) нач знач:= нет если x * x + y * y <= a * a то знач:= да все кон |
Замечание. Предложенные компьютерные модели можно использовать для вычисления числа π, если при выполнении программ задавать радиус круга равный единице. Программы можно дополнить имитацией «бросания» точек в квадрат и вычислением времени счета.
Компьютерная модель на языке Turbo Delphi
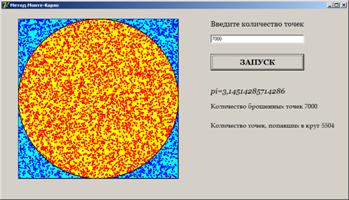
Предлагается программа вычисления числа π на Turbo Delphi с имитацией «бросания» точек в квадрат (рис. 14). Проанализируйте решение задачи с целью определения логической структуры компьютерной модели, выбора компонентов для описания отдельных блоков компьютерной модели, понимания механизмов реализации этих блоков.
|
| Рис. 14 |
procedure TForm1.Edit1KeyPress(Sender: TObject; var Key: Char);
begin
//ограничение, чтобы в текстовое поле могли быть введены только числа,
//также могут быть нажаты клавиши Enter и BackSpace
if (not (key in ['0','1','2','3','4','5','6','7','8','9'])) and (key<>#13) and(key<>#8) then
begin
showmessage('Могут быть введены только цифры'); key:=#0;
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
var n,k,i:longint; x,y:integer; pi:real;
begin
randomize;
image1.Canvas.pen.Color:=clBlack; image1.Canvas.Pen.Width:=2;
image1.Canvas.Pen.Style:=psSolid; image1.Canvas.Brush.Color:=claqua;
image1.Canvas.Brush.Style:=bsSolid; image1.canvas.Rectangle(0,0,400,400);
image1.Canvas.Brush.Color:=clyellow; image1.Canvas.Ellipse(0,0,400,400);
Application.ProcessMessages; image1.Canvas.Pen.Width:=1;
if edit1.text<>'' then
begin
n:=strtoint(edit1.Text); //количество точек, бросаемых в квадрат
k:=0; //количество точек, попавших в круг
for i:=1 to n do
begin
//задание координат точек случайным образом
x:=random(400); y:=random(400);
if (sqr(x-x0)+sqr(y-y0)<=sqr(r)) then
begin
k:=k+1;
image1.Canvas.Pen.color:=clRed; image1.canvas.Brush.Color:=clred;
image1.Canvas.Ellipse(x-2,y-2,x+2,y+2);
image1.Canvas.FloodFill(x,y,clRed,fsborder);
//для постепенного заполнения точками области квадрата
if i mod 50 =0 then Application.ProcessMessages;
end
else
begin
image1.Canvas.Pen.Color:=clBlue; image1.canvas.Brush.Color:=clblue;
image1.Canvas.Ellipse(x-2,y-2,x+2,y+2);
image1.Canvas.FloodFill(x,y,clBlue,fsborder);
if i mod 50 =0 then Application.ProcessMessages; end; //end if
pi:=4*k/i;
//вывод полученного значения pi
label2.Caption:='pi='+floattostr(pi);
label3.Caption:= 'Количество брошенных точек '+inttostr(i);
label4.Caption:='Количество точек, попавших в круг '+inttostr(k);
end; //end for
end
else
ShowMessage('введите количество точек');
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
//задание размеров области рисования
image1.Height:=400; image1.Width:=400;
x0:=image1.width div 2; y0:=image1.height div 2; r:=image1.Height div 2;
//прорисовка начального состояния области
image1.Canvas.pen.Color:=clBlack; image1.Canvas.Pen.Width:=2;
image1.Canvas.Pen.Style:=psSolid; image1.Canvas.Brush.Color:=claqua;
image1.Canvas.Brush.Style:=bsSolid; image1.canvas.Rectangle(0,0,400,400);
image1.Canvas.Brush.Color:=clyellow; image1.Canvas.Ellipse(0,0,400,400);
end;
6-7-й этапы. Вычислительный эксперимент, анализ результатов эксперимента. Для проведения вычислительного эксперимента выберите радиус круга равным единице. Площадь круга в этом случае будет равна π, результат работы программы – число π.
Результаты эксперимента оформите в виде таблицы:
| n | … | … | |||
| π | … | … |
Замечание. Рассмотренные в пункте 9.2.2 математические модели являются вероятностными. Результаты, полученные с их помощью, подчиняются закону больших чисел, то есть в данном случае точность в определении площади зависит от количества n брошенных случайно точек. При большом количестве брошенных случайно точек площадь круга единичного радиуса приближается к значению π.
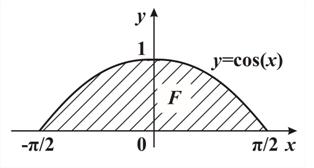
Пример 4. 1-й этап. Постановка задачи. Составьте компьютерную модель для вычисления площади фигуры F, изображенной на рис. 15. Проведите анализ предложенных решений задачи: вспомните схему этапов составления компьютерной модели объекта, выделите цели реализации этих этапов, определите, достигнуты ли эти цели в предложенных решениях.
| 
|
| Рис. 15 |
2-й этап. Анализ объекта моделирования и построение информационной модели. Поместим фигуру F в прямоугольник ADCB наименьшего размера, площадь которого легко вычислить:
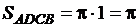 .
.
Будем бросать в прямоугольник n случайных точек и определять число m – число точек, попавших внутрь фигуры F. Составим информационную модель процесса нахождения площади фигуры F с использованием метода Монте-Карло.
Результат и исходные данные связаны между собой соотношением 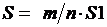 , где S – площадь искомой фигуры F, а S 1– площадь прямоугольника. К связям между исходными данными и результатом следует отнести и математические соотношения, позволяющие определить, попала ли выбранная точка в фигуру F.
, где S – площадь искомой фигуры F, а S 1– площадь прямоугольника. К связям между исходными данными и результатом следует отнести и математические соотношения, позволяющие определить, попала ли выбранная точка в фигуру F.
Точка принадлежит прямоугольнику ADCB, если выполняются соотношения
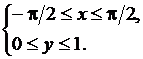
Точка принадлежит фигуре F, если выполняются соотношения
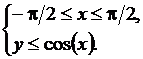
3-4-й этапы. Алгоритмизация решения задачи и создание компьютерной модели. Выберем исполнителя Ершол–систему. Получить случайное вещественное число х в диапазоне 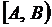 можно по формуле х:=(B–A)*rnd(1)+A. Получить случайное вещественное число х в диапазоне
можно по формуле х:=(B–A)*rnd(1)+A. Получить случайное вещественное число х в диапазоне 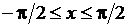 можно операторами присваивания pi:=4*arctg(1); х:=pi*rnd(1)-pi/2. Получить случайное вещественное число y в диапазоне
можно операторами присваивания pi:=4*arctg(1); х:=pi*rnd(1)-pi/2. Получить случайное вещественное число y в диапазоне 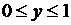 можно оператором присваивания y:=rnd(1).
можно оператором присваивания y:=rnd(1).
Программа на языке Ершол.
алг площадь
начцел n,i,m, вещ s,x,y,pi
вывод "Введите количество бросаемых точек "; ввод n
pi:=4*arctg(1); m:=0
нцдля i от 1 до n
x:=pi*rnd(1.000001)-pi/2; y:=rnd(1.000001)
если y<=cos(x)
то m:=m+1
все
кц
s:=(m/n)*pi
вывод "Площадь фигуры F равна ",s
выводнс, "Точное значение площади фигуры F равно",2
кон
6-7-й этапы. Вычислительный эксперимент, анализ результатов эксперимента. Вычислим площадь фигуры F, используя формулу Ньютона-Лейбница: 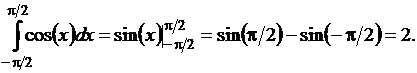
Результаты эксперимента оформите в виде таблицы.
| n | … | … | |||
| S | … | … |
Сравните результаты вычислений по формуле 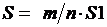 с точным результатом
с точным результатом 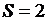 , полученным при решении задачи с использованием формулы Ньютона-Лейбница.
, полученным при решении задачи с использованием формулы Ньютона-Лейбница.
Выполнение этапов 2 – 7 для решения поставленной задачи с использованием приближённого нахождения площади криволинейной трапеции методом серединных прямоугольников [1].
2-й этап. Анализ объекта моделирования и построение информационной модели. Требуется приближённо вычислить площадь фигуры, ограниченной графиком непрерывной функции 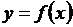 , где
, где 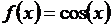 и
и  , прямыми
, прямыми  ,
, 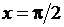 ,
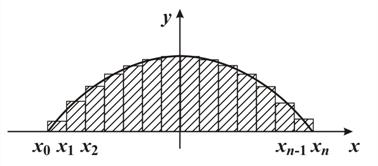
,  , рис. 16. Фигура, изображенная на рис. 16, является криволинейной трапецией.
, рис. 16. Фигура, изображенная на рис. 16, является криволинейной трапецией.
|
| Рис. 16 |
Отрезок 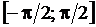 разобьём на n элементарных отрезков длины h точками
разобьём на n элементарных отрезков длины h точками 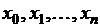 ,
, 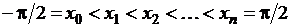 .
.
Введём обозначение 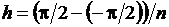 или
или 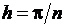 . На каждом из полученных отрезков
. На каждом из полученных отрезков 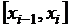 построим прямоугольник, одной стороной которого будет отрезок
построим прямоугольник, одной стороной которого будет отрезок 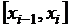 , а другой – отрезок, длина которого равна
, а другой – отрезок, длина которого равна 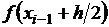 ,
,  .
.
Площадь криволинейной трапеции можно приближённо считать равной сумме площадей заштрихованных прямоугольников, построенных на каждом из отрезков деления. Для заданной функции площадь вычисляется по формуле серединных прямоугольников так:
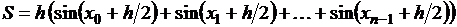 ,
,
где 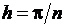 ,
, 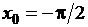 ,
, 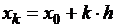 .
.
3-4-й этапы. Алгоритмизация решения задачи и создание компьютерной модели. Ершол–систему выберем исполнителем программы. Составим для исполнителя программу вычисления площади фигуры F для фиксированного значения n.
алг площадь
начцел n, вещ s, x, pi, h
вывод "Введите количество разбиений отрезка [-pi / 2, pi / 2] "
ввод n
pi:= 4 * arctg (1); h:= pi / n; x:= -pi / 2 – h / 2; s:= 0
нцпока x <= pi / 2 - h / 2
x:= x + h; s:= s + h * f(x)
кц
вывод "Площадь фигуры F равна ", s
выводнс, "Точное значение площади фигуры F равно",2
кон
алгвещ f (аргвещ x)
нач
знач:= cos(x)
кон
Результаты эксперимента оформите в виде таблицы:
| n | … | … | |||
| Sn | … | … | |||
| S т. |
Сравните результаты вычислений площади фигуры F с использованием формулы серединных прямоугольников для фиксированного n с точным результатом 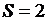 , полученным при решении задачи с использованием формулы Ньютона – Лейбница. Вычислительный эксперимент показывает, что с увеличением n, числа разбиений отрезка
, полученным при решении задачи с использованием формулы Ньютона – Лейбница. Вычислительный эксперимент показывает, что с увеличением n, числа разбиений отрезка 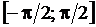 , площади фигуры F, вычисленные по приближенной формуле, мало отличаются друг от друга.
, площади фигуры F, вычисленные по приближенной формуле, мало отличаются друг от друга.
Составим программу для вычисления площади фигуры F с точностью e методом серединных прямоугольников. Для вычисления площади фигуры F с заданной точностью воспользуемся способом, предложенным в примерах 1, 2. Вычисление площади фигуры F выполняется два раза с заданным числом разбиений n и числом разбиений 2 n. Проверяется условие 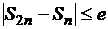 [2], если оно истинно, то за значение площади фигуры F берётся значение
[2], если оно истинно, то за значение площади фигуры F берётся значение 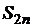 ,и вычисления заканчиваются. Если условие ложно, то число разбиений снова удваивается, переменная
,и вычисления заканчиваются. Если условие ложно, то число разбиений снова удваивается, переменная 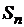 принимает значение
принимает значение 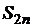 , вычисляется значение площади фигуры F при вновь удвоенном n, и это значение присваивается переменной
, вычисляется значение площади фигуры F при вновь удвоенном n, и это значение присваивается переменной 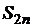 , проверяется выполнение условия
, проверяется выполнение условия 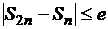 и т. д. до тех пор, пока проверяемое на каждом шаге условие не будет истинным.
и т. д. до тех пор, пока проверяемое на каждом шаге условие не будет истинным.
Программа для приближённого вычисления площади с заданной точностью:
алг площадь1
начцел n, вещ s1, s, e, s2
вывод "Введите количество разбиений отрезка [-pi / 2,pi / 2] "; ввод n
выводнс,"Введите точность вычисления e "; ввод e
площадь(n, s); s1:= s; n:= n * 2;площадь(n, s); s2:= s
нцпока abs(s1- s2) > e
s1:= s2; n:= 2*n; площадь(n, s); s2:= s
кц
вывод "Площадь фигуры F равна ", s1
выводнс, "Точное значение площади фигуры F равно", 2
кон
алг площадь (аргцел n, рез вещ s)
начвещ x, pi, h
pi:=4 * arctg(1); h:= pi / n; x:= -pi / 2 – h / 2; s:= 0
нцпока x <= pi / 2 – h / 2
x:= x + h; s:= s + h * f(x)
кц
кон
алгвещ f (аргвещ x)
нач
знач:= cos(x)
кон
Результаты эксперимента оформите в виде таблицы
| e | … | … | |||
| S2n | … | … | |||
| S т. | … |
Пример 5. Задача о встрече. 1-й этап. Постановка задачи. Каждый день резидент приходит на встречу со своим агентом в случайный момент времени с 13 до 14 часов и ждет его 20 минут, после чего уходит. В свою очередь агент приходит на встречу с резидентом каждый день также в случайный момент времени с 13 до 14 часов и тоже ждет 20 минут, после чего уходит. Какова вероятность встречи этих лиц, если каждый в течение часа приходит к этому месту наудачу и моменты прихода независимы друг от друга?
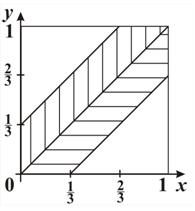
|
| Рис. 17 |
2-й этап. Анализ объекта моделирования и построение информационной модели. Изобразим исходы испытаний на координатной плоскости. На прямой Ox от точки O (0,0) отложим отрезок, равный единице длины, принимая за единицу масштаба один час, – это время прихода резидента. На прямой Oy от точки O (0,0) тоже отложим отрезок, равный единице длины – это время прихода агента. Тогда множество всех возможных исходов испытания можно изобразить точками квадрата, сторона которого равна единице. Встреча произойдет лишь в том случае, если разность моментов прихода резидента и агента по абсолютной величине не будет превосходить  часа (двадцати минут), т. е. если произойдет событие, удовлетворяющее неравенству
часа (двадцати минут), т. е. если произойдет событие, удовлетворяющее неравенству 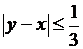 .
.
Запишем это неравенство в виде системы неравенств:
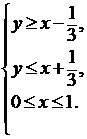
Эта система неравенств задает заштрихованную область на рис. 17. Искомая вероятность равна отношению площади заштрихованной области к площади квадрата.
3-4-й этапы. Алгоритмизация решения задачи и создание компьютерной модели.
1 способ нахождения вероятности встречи резидента и агента. Для получения результата воспользуемся точными формулами вычисления площадей:
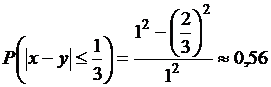 .
.
2 способ нахождения вероятности встречи резидента и агента. Воспользуемся для решения задачи методом Монте-Карло. Будем многократно бросать в квадрат случайные точки (песчинки). Обозначим через n количество точек, брошенных в квадрат, через m – количество точек, попавших при этом внутрь заштрихованной фигуры. Геометрически очевидно, что отношение площадей 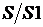 , где S – площадь заштрихованной фигуры, приближенно равно отношению
, где S – площадь заштрихованной фигуры, приближенно равно отношению 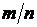 . Отношение площадей фигур заменим отношением
. Отношение площадей фигур заменим отношением 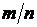 . При большом количестве брошенных случайно точек вероятность встречи агента и резидента будет вычислена точнее.
. При большом количестве брошенных случайно точек вероятность встречи агента и резидента будет вычислена точнее.
Составим компьютерную модель для исполнителя Turbo Pascal.
| Program meeting; uses crt; Var I,n,m: longint; x,y,k: real; Begin write ('Введите количество бросаемых точек n '); readln (n); i:=1;m:=0; Randomize; While i<=n do begin | x:=random; y:=random; If abs(x-y)<=1/3 then m:=m+1; i:=i+1; end; k:=m/n*1; writeln(' вероятность встречи = ',k); writeln(1-4/9); end. |
6-7-й этапы. Вычислительный эксперимент, анализ результатов эксперимента.
Результаты эксперимента оформите в виде таблицы:
| n | … | … | |||
| P | … | … |
Сравните результаты вычислений с результатом, полученным при решении задачи первым способом P ≈ 0,56.
Изложенные выше теоретический материал и методы решения жизненных задач можно использовать при подготовке к семинарским и лабораторно-практическим занятиям по данной теме.
10. Вопросы и задания к семинарским занятиям
Тема «Моделирование и формализация. Вычислительный эксперимент»
Выполните задания 1, 2, 3, 4, 5, 6, ответьте на вопросы, поставленные в этих заданиях. Доложите результаты выполнения данных заданий в студенческой аудитории в форме презентации.
1. Определите место и роль темы «Моделирование и формализация. Вычислительный эксперимент» в решении общеобразовательных задач предмета «Информатика и ИКТ». Какое место и роль отводят авторы учебных пособий данной теме и почему? Какое место и роль отвели бы Вы? Выбор обоснуйте. Как менялось со временем место, роль и содержание данной темы?
2. Проведите сравнительный дидактический анализ содержания учебного материала по данной теме в различных учебниках и учебных пособиях по предмету «Информатика и ИКТ» для общеобразовательных учреждений на каждой ступени непрерывного курса изучения информатики: начальный курс (II – VI классы), базовый курс (VII – IX классы), профильный курс обучения (X – XI классы). Соотнесите содержание учебного материала с требованиями государственного стандарта образования по информатике.
3. Сформулируйте цели и задачи, стоящие перед учителем в процессе организации изучения школьниками данной темы на каждой ступени непрерывного курса изучения информатики. Какие учебные цели соответственно должны стоять перед учащимися?
4. Проанализируйте программное обеспечение к теме «Моделирование и формализация. Вычислительный эксперимент» как средство получения учащимися предполагаемых знаний, умений и навыков. Определите дидактические цели использования каждого выбранного программного обеспечения при изучении темы. Выделите основные методы и способы составления компьютерных моделей и проведения вычислительного эксперимента при решении задач с использованием выделенного программного обеспечения.
5. Выявите базовые понятия темы «Моделирование и формализация. Вычислительный эксперимент», определите этапы, формы и методы их формирования, установите отношения между выделенными понятиями. Составьте терминологический словарь по базовым понятиям темы. Определите общеобразовательный и мировоззренческий аспекты базовых понятий темы.
6. Отберите содержание учебного материала по теме «Моделирование и формализация. Вычислительный эксперимент» в соответствии с особенностями развития школьника на выбранном конкретном возрастном этапе. Составьте логико-структурную модель учебного материала по теме на выбранной ступени непрерывного курса изучения информатики.
7. Отберите содержание учебного материала и разработайте конспект одного урока по предложенным ниже темам на выбранной ступени непрерывного курса изучения информатики. Апробируйте в студенческой аудитории разработанный конспект урока.
7.1. «Компьютерное моделирование»; «Формализация, как процесс построения информационных моделей»; «Вычислительный эксперимент с использованием компьютера».
7.2. «Понятие модели, цели создания моделей, классификация моделей по различным признакам».
7.3 «Доказательство адекватности модели изучаемому объекту, процессу».
8. Подберите практическую задачу на выбранной ступени непрерывного курса изучения информатики и на её основе разработайте фрагмент урока по теме «Этапы решения задач с использованием компьютера». Выделите цели каждого этапа. Защитите свои разработки в студенческой аудитории.
9. Сконструируйте серию уроков по изучению содержательной линии «Моделирование и формализация», в которых для составления информационных моделей используются
9.1. метод дискретизации непрерывных процессов;
9.2. метод Монте-Карло – моделирование с использованием случайных величин.
Апробируйте в студенческой аудитории фрагмент одного из разработанных уроков по указанным темам.
10. На основе классификации компьютерных моделей предложите типологию задач, используемых в процессе изучения данной содержательной линии на выбранной ступени непрерывного курса изучения информатики. Защитите свои разработки по классификации задач в студенческой аудитории.
11. Проанализируйте дидактические возможности учебного материала содержательной линии «Моделирование и формализация» на каждой ступени непрерывного курса изучения информатики для реализации задач:
11.1. формирования системно-информационных представлений и информационной культуры учащихся, в процессе изучения информатики (понимания, что моделирование – метод научного познания, понимания сущности метода информационного моделирования, умения строить информационные модели с помощью формальных языков – навыки формализации, умения структурировать изучаемый объект, понимания смысла отношения объект – модель);
Date: 2015-07-17; view: 751; Нарушение авторских прав