
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Требования к уровню подготовки учащихся 4 page
|
|
11.2. развивающего обучения.
Доложите результаты своего дидактического анализа в студенческой аудитории.
11. Лабораторно-практическая работа
Тема «Моделирование и формализация. Вычислительный эксперимент»
Используйте для решения задач исполнителей: Ершол, QBasic, Turbo Pascal, Visual Basic.Net, Turbo Delphi, Microsoft Excel и др.
Для решения задач 1, 2, 3 составьте компьютерные модели, рассмотрев все этапы реализации компьютерных моделей, для составления информационных моделей используйте метод дискретизации непрерывных процессов. Смотрите примеры 1, 2 теоретической части. Проведите презентацию своей работы в студенческой аудитории.
Задача 1. Выполняя утреннюю зарядку, школьник подошел к стене, на которой был закреплен пружинный эспандер, и оттянул его на некоторое расстояние. Какую работу совершила при этом сила натяжения пружины [14]?
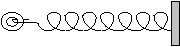 |
Указание к решению. При построении математической модели для этой задачи сделайте следующие предположения: сила натяжения пружины подчинена закону Гука; если весь промежуток движения тела разбить на большое число равных маленьких промежутков, то можно считать, что сила на каждом из них постоянна и меняется «мгновенно» в конце каждого промежутка; при неограниченном увеличении числа этих промежутков величина работы получается с любой точностью.
Задача 2. Плотина прямоугольной формы перегораживает реку. Определить силу давления воды на плотину [14].
 |
Задача 3. Тело падает с высоты h м, необходимо определить время падения тела с учетом сопротивления. Экспериментально установлено, что сила сопротивления воздуха пропорциональна квадрату скорости, а коэффициент зависит от формы тела. Поэтому ускорение падающего тела вычисляется по формуле 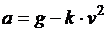 , где k – коэффициент, зависящий от массы и формы тела (для человека среднего роста и веса
, где k – коэффициент, зависящий от массы и формы тела (для человека среднего роста и веса 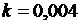 ). Для простоты будем считать, что падение происходит на планете с ускорением свободного падения
). Для простоты будем считать, что падение происходит на планете с ускорением свободного падения 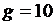 м/с2. Смотрите пример 2 теоретической части пособия.
м/с2. Смотрите пример 2 теоретической части пособия.
Для решения задач 4 – 9 составьте компьютерные модели, рассмотрев все этапы решения задач с использованием компьютера, используйте для составления информационных и компьютерных моделей метод Монте-Карло. Проведите вычислительный эксперимент, результаты работы программ соотнесите с теоретическими результатами. Смотрите примеры 3 – 5 теоретической части. Проведите презентацию своей работы в студенческой аудитории.
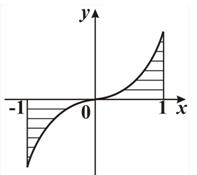
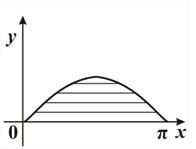
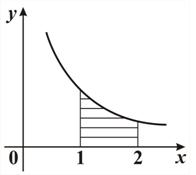
Задача 4. Составьте компьютерные модели вычисления площадей заштрихованных областей фигур, изображенных на рис. 18.
| 
| 
|
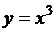
| 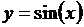
| 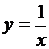
|
| Рис. 18 |
Задача 5. Дано линейное уравнение 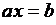 . Если a выбирается наудачу на отрезке
. Если a выбирается наудачу на отрезке 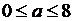 , b – на отрезке
, b – на отрезке 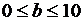 , то какова вероятность того, что корень данного уравнения будет больше единицы? Предполагается, что вероятность попадания точки в плоскую фигуру пропорционально площади фигуры и не зависит от её расположения.
, то какова вероятность того, что корень данного уравнения будет больше единицы? Предполагается, что вероятность попадания точки в плоскую фигуру пропорционально площади фигуры и не зависит от её расположения.
Задача 6. Два действительных числа x и y выбираются наугад так, что сумма их квадратов меньше 100. Какова вероятность того, что сумма квадратов x и y окажется больше 64? Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади фигуры и не зависит от её расположения.
Задача 7. На отрезке OA длины L числовой оси Ox наудачу поставлены две точки B(x) и C(y), причём 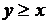 . Найдите вероятность того, что длина отрезка BC будет меньше длины отрезка OB. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине этого отрезка и не зависит от его расположения на числовой оси.
. Найдите вероятность того, что длина отрезка BC будет меньше длины отрезка OB. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине этого отрезка и не зависит от его расположения на числовой оси.
Задача 8. На отрезке OA длины L числовой оси Ox наудачу поставлены две точки B(x) и C(y). Найдите вероятность того, что из трёх получившихся отрезков можно построить треугольник.
Задача 9. Два студента условились встретиться на площади у фонтана между 15 и 17 часами дня. Студент, пришедший первым, ждёт второго в течение 1/2 часа, после чего уходит. Найдите вероятность того, что встреча состоится, если каждый студент наудачу выбирает время своего прихода (в промежутке от 15 до 17 часов).
12. Самостоятельная работа
Тема «Моделирование и формализация. Вычислительный эксперимент»
Используйте для решения задач исполнителей: Ершол, QBasic, Turbo Pascal, Visual Basic.Net, Turbo Delphi, Microsoft Excel и др.
Для выполнения заданий 1, 2, 3 разработайте и реализуйте с использованием выбранного исполнителя учебные проекты в виде компьютерных моделей, рассмотрев все этапы составления компьютерных моделей. Подготовьте проекты к защите.
Задание 1. Компьютерная модель «Электронный кассир»
Пусть в кинозале 24 ряда по 35 мест, а цена билета зависит только от номера ряда. Составьте программу, которая могла бы имитировать продажу билетов в кинозал:
– высвечивать информацию о проданных и свободных местах на данный сеанс;
– осуществлять поиск одного, двух, трех свободных мест;
– производить расчёт с посетителем при покупке билетов;
– подсчитывать выручку;
– обновлять табло с информацией о свободных местах после продажи билетов посетителю.
Задание 2. Компьютерная модель «Гараж»
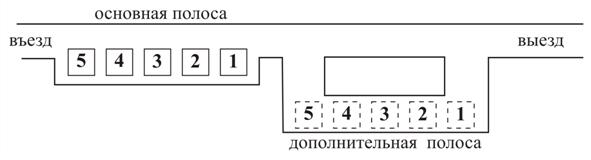
Гараж содержит одну полосу, на которой может быть размещено до n автомашин. Автомобили въезжают в гараж с запада, а покидают его с восточного конца. Если автомобиль владельца, пришедшего забрать автомобиль, не расположен восточнее всех остальных, то все автомобили, стоящие восточнее этой машины, удаляются из гаража на запасную полосу, затем выезжает машина владельца, пришедшего забрать автомобиль (рис. 19). Машины с запасной полосы помещаются назад на свои места. Все машины, расположенные западнее выехавшей машины, сдвигаются на восток столько раз, сколько имеется свободных позиций в восточной части.
|
| Рис. 19 |
Указания к выполнению задания (предполагаемые технические требования).
· Программа начинается с заставки, где указываются некоторые сведения о программе и авторе программы.
· В диалоговом режиме программа запрашивает число автомобилей в гараже и их номера.
· На экране должна отражаться динамика заполнения гаража машинами.
· Программа должна запрашивать номер машины, которая покидает гараж.
· На экране отображается динамика всех перемещений автомобилей.
Задание 3. Выбор места строительства железнодорожной станции.
В одном районе расположены три населенных пункта. По территории района проходит железная дорога. По просьбе жителей района планируется построить железнодорожную станцию и проложить дороги от нее до каждого населенного пункта. Требуется определить наиболее удобное расположение железнодорожной станции. Место для станции надо выбрать так, чтобы наибольшее из расстояний от неё до населённых пунктов было как можно меньше.
Указание к выполнению задания. Выберите систему координат так, чтобы ось абсцисс проходила по интересующему нас участку железной дороги, а начало координат совпало с левым концом дороги. Для составления информационной модели примените метод дискретизации непрерывных процессов, разбейте отрезок [0; S ] на n равных частей, S – длина отрезка, изображающего на карте участок железной дороги, пролегающий по рассматриваемой местности.
Выполните задания 4, 5, 6. Проделанную и оформленную работу подготовьте для защиты.
Задание 4. Составьте поурочный план изучения данной темы по предмету «Информатика и ИКТ» на одной из ступеней непрерывного курса изучения информатики.
Задание 5. Разработайте тематику, содержание, методы и приёмы проведения лабораторных работ по теме «Моделирование и формализация. Вычислительный эксперимент» на каждой ступени непрерывного курса изучения информатики.
Задание 6. Разработайте сценарии программ (демонстрационных, обучающих, тренажеров, контролирующих) по данной теме и реализуйте один проект на выбранном программном обеспечении.
Глава 2. Графы и компьютерное моделирование
«Теория графов предоставляет очень удобный язык для описания программных (да и многих других) моделей. Стройная система специальных терминов и обозначений теории графов позволяют просто и доступно описывать сложные и тонкие вещи. Особенно важно наличие наглядной графической интерпретации понятия графа. Картинки позволяют сразу «усмотреть» суть дела на интуитивном уровне, дополняя и украшая утомительные рациональные текстовые доказательства и сложные формулы»
Ф. А. Новиков
Методы решения задач с использованием теории графов позволяют учащимся получить опыт построения и исследования моделей реальных объектов на компьютере. Для успешного применения теории графов при решении задач необходимо научить школьников видеть в условии задачи структуру графа и грамотно переводить это условие на язык теории графов.
1. Мотивационные задачи к введению понятия «граф»
Задача 1. Между девятью планетами Солнечной системы введено космическое сообщение, ракета летает по следующим маршрутам: Земля – Меркурий, Плутон – Венера, Земля – Плутон, Плутон – Меркурий, Меркурий – Венера, Уран – Нептун, Нептун – Сатурн, Сатурн – Юпитер, Юпитер – Марс, Марс – Уран. Можно ли долететь от Земли до Марса?
Решение. Объектом исследования является часть Солнечной системы. Проведём системный анализ объекта. Выделим элементы системы, это планеты. Установим связь между элементами: две планеты взаимосвязаны, если между ними установлено космическое сообщение. Нарисуем схему: планеты обозначим точками, а соединяющие их маршруты линиями (рис. 20).
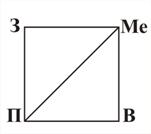
| 
|
| Рис. 20 |
Так как нет ломаной линии, соединяющей Землю и Марс, то можно сделать вывод, что долететь от Земли до Марса при данном сообщении нельзя.
Задача 2. Задача о перестановке четырёх коней (рис. 21), исполнитель – Конюх. Напишите алгоритм перестановки коней из начального положения в конечное.
|
| ||||||||||||||||||||||||||||||||
| Начальное положение | Конечное положение | ||||||||||||||||||||||||||||||||
| Рис. 21 |
Конь перемещается за один ход либо на два поля по вертикали и одно поле по горизонтали, либо на два поля по горизонтали и одно по вертикали (буквой «Г»). Конь может перепрыгивать через стоящие на его пути другие фигуры, но может ходить в нашей задаче только на свободные поля. Составьте для решения задачи графическую информационную модель.
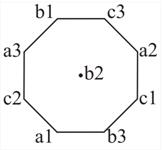
Решение. Объектом исследования является клетчатое поле 3´3. Проведем системный анализ объекта. Выделим элементы системы – клетки поля. Установим связь между элементами: две клетки взаимосвязаны, если из одной клетки в другую можно попасть ходом шахматного коня. Изобразим клетки поля точками, если из одной клетки поля можно попасть в другую ходом шахматного коня, то соединим эти клетки отрезком прямой.
| 
| 
|
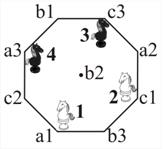
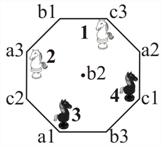
| Начальное положение | Конечное положение | |
| Рис. 22 |
Начальная и конечная расстановки коней изображены на рис. 22. Написание алгоритма перестановки коней для исполнителя Конюха становится очевидным.
Задача 3. Задача о Кёнигсбергских мостах (см. с. 16).
Задача 4. На встрече группы хорошо и не очень хорошо знакомых делегатов конгресса по информатике состоялось много приветственных рукопожатий. Некоторые делегаты пожали четное число рук, другие – нечетное. Например, Сергей обменялся тремя рукопожатиями, а его друг, Николай, – девятью. Когда Сергей сказал своему другу, что обменявшихся нечетным числом рукопожатий, кроме Сергея и Николая, было еще 5 человек, он ответил: ошибаешься. Число людей, пожавших нечетное число рук, непременно должно быть чётным. Прав ли он? Объясните свои выводы.
Задача 5. В некоторой стране 110 городов, между некоторыми из них летают самолеты. Авиатрассы расположены так, что из любого города можно перелететь в другой (возможно с пересадками). Определите, можно ли из города А добраться в город В, делая не более 1, 2 или 3 пересадок. Составьте информационную и компьютерную модели для решения поставленной задачи.
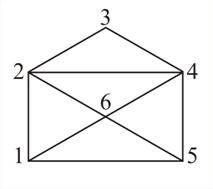
Задача 6. Уникурсальной называется линия, которую можно построить, не отрывая карандаша от бумаги и не проходя дважды по одному и тому же звену. Дана линия. Разработайте компьютерную модель, которая определяет, является ли данная линия уникурсальной, и выводит на экран один из маршрутов обхода линии, удовлетворяющий условию задачи (рис. 23).
|
| Рис. 23 |
2. Некоторые понятия теории графов
Графом G называют пару множеств (W,E), где W – это непустое конечное множество элементов, которое мы назовём вершинами графа, а E – это конечное множество неупорядоченных или упорядоченных пар элементов множества W. Элементы множества E –рёбра или дуги. Неупорядоченную пару вершин { V, U } будем называть ребром, а упорядоченную пару назовем дугой < V, U > (V – начало дуги, U – конец дуги). При изображении графов на рисунках рёбра и дуги будем изображать линиями, у дуг на концах будем изображать стрелки, указывающие направление связи вершин, вершины – точками, окружностями или квадратами. Такое представление графа называется диаграммой. Диаграмма графа – это информационная модель объекта, это информация о составе и структуре системы, представленная в графической форме.
Граф, содержащий только рёбра, называется неориентированным графом. Граф, содержащий только дуги, называется ориентированным графом, или орграфом. Мощности множеств W и E будем обозначать соответственно n и m (n – количество вершин, m – количество рёбер). Обычно вершины обозначаются заглавными буквами русского или латинского алфавита или числами, рёбра обозначаются парами вершин или строчными буквами русского и латинского алфавита. Когда берем пару вершин { V, U }, то будем говорить, что ребро соединяет вершины V и U. Две вершины U и V графа G называются смежными, если существует соединяющее их ребро { U, V }. При этом вершины U и V называются инцидентными этому ребру, а ребро инцидентным этим вершинам. Два ребра называются смежными, если они имеют, по крайней мере, одну общую вершину. В орграфе вершина U называется смежной вершине V, если существует дуга < U, V >. При этом вершины U и V называются инцидентными дуге < U, V >, а дуга – инцидентной соответствующим вершина м.
Примеры
|
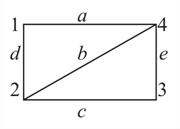
| Рис. 24 |
|
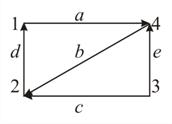
| Рис. 25 |
Неориентированный граф (рис. 24)
W = {1, 4, 3, 2}
E = { a, b, c, d, e }
E = {{1, 4}, {2, 4}, {2, 3}, {1, 2}, {3, 4}}
Мощности: n = 4, m = 5.
Ориентированный граф (рис. 25)
W = {1, 4, 3, 2}
E = {<2, 1>, <3, 2>, <3, 4>, <1, 4>, <4, 2>}
n = 4, m = 5.
Степенью вершины называется число рёбер графа, которым принадлежит эта вершина. Вершина графа, имеющая нечётную степень, называется нечётной вершиной. Вершина графа, имеющая чётную степень – чётной вершиной. Вершина графа, имеющая степень 0, называется изолированной. Вершина графа, имеющая степень 1, называется висячей.
Теорема. Число нечётных вершин любого графа – число чётное.
Задача 7. В классе 25 человек. Может ли быть так, что 7 из них имеют по три друга в этом классе, 11– по 4 друга, а 7 – по 5 друзей.
Решение. Граф имеет 25 вершин, 7 из них имеют по три ребра – степень 3, 10 – степень 4 и 8 – степень 5. Нечетных вершин – 15, такого быть не может!
Теорема. В графе G сумма степеней всех его вершин – число чётное, равное удвоенному числу рёбер графа.
Задача 8. В посёлке Бессвязном всего 7 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с тремя другими?
Решение. (3·7)/2 – нецелое число, (нельзя).
Путём от вершины U к вершине V в графе называется такая последовательность рёбер, ведущая от U к V, в которой каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается более одного раза. Вершина U – начало пути, а вершина V – конец пути. Путь от U к V называется простым, если он не проходит ни через одну из вершин более одного раза.
|
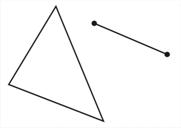
| Рис. 26 |
Две вершины U и V называются связными, если в графе существует путь с концами U и V. Две вершины графа называются несвязными, если в графе не существует пути, связывающего их.  Граф называется связным, если каждые две вершины его связные, в противном случае граф называется несвязным.
Граф называется связным, если каждые две вершины его связные, в противном случае граф называется несвязным.
На рис. 24 граф связный, а на рис. 26 – несвязный, состоит из трех связных компонентов.
Эйлеров путь
Эйлеров путь – это произвольный путь в графе, проходящий через каждое ребро графа в точности один раз, т. е. путь 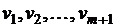 , такой, что каждое ребро
, такой, что каждое ребро 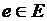 появляется в этом пути ровно один раз как ребро
появляется в этом пути ровно один раз как ребро 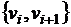 , где
, где 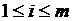 . Эйлеров цикл – это эйлеров путь, где начало пути совпадает с концом. В 1736 году Эйлер доказал первую теорему теории графов, теорему о необходимом и достаточном условии существования эйлерова пути.
. Эйлеров цикл – это эйлеров путь, где начало пути совпадает с концом. В 1736 году Эйлер доказал первую теорему теории графов, теорему о необходимом и достаточном условии существования эйлерова пути.
Программы нахождения эйлерова цикла приведены на с. 126.
Теорема. Эйлеров путь в связном неориентированном графе существует тогда и только тогда, когда граф содержит не более чем две вершины нечетной степени.
Если граф содержит эйлеров путь, или эйлеров цикл, то диаграмма графа – уникурсальная линия.
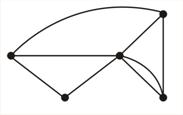
Задача 9. Определите, являются ли диаграммы графов на рис. 27, а и 27, б уникурсальными линиями.
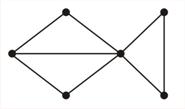
| 
|
| а) | б) |
| Рис. 27 |
3. Машинное представление графов
В настоящее время почти в каждой отрасли науки и техники встречаются задачи, для решения которых используется теория графов. Например, в электротехнике – при построении электрических схем, в биологии – при исследовании биологических систем, в экономике – при решении задач о выборе оптимального пути для потока грузового транспорта. С теорией графов связаны такие серьезные науки, как теория относительности, теория групп. Важным вопросом, особенно для приложений теории графов, является определение возможных способов представления графов. Граф можно представить в виде диаграммы, отражающей смежность вершин, и визуально определить некоторые свойства и характеристики заданного графа. Однако при наличии в графе большого числа рёбер и вершин этот способ мало пригоден. У нас есть верный помощник, обладающий огромным быстродействием, это компьютер. Поэтому необходимо научиться представлять структуру графа в компьютере. Каким же образом предпочтительнее представлять информацию об исследуемом объекте в виде графа в компьютере? Современные технические средства допускают ввод информации в компьютер в различных формах. Выбор подходящей структуры данных для представления графа в компьютере имеет принципиальное значение при разработке эффективных алгоритмов. Способов представления графа в памяти компьютера множество, но все они основаны на базовых представлениях. Мы рассмотрим три способа представления графов в памяти компьютера в числовом виде.
Способы представления графов в памяти компьютера: матрица инцидентности, матрица смежности, перечень рёбер.
3.1. Матрица смежности
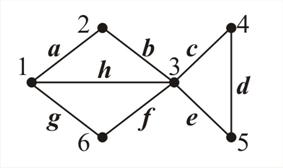
На рис. 28 представлена диаграмма графа. Диаграмма отражает смежность вершин в графе. Распространенным способом структурирования данных является также прямоугольная таблица. Преобразуем структуру данных и связей объекта, представленных в виде диаграммы, в табличную форму. Заменим диаграмму двоичной таблицей типа «объект-объект», отражающей качественную связь между объектами – смежность вершин графа (есть связь или нет связи) (рис. 29).
|
| |||||||||||||||||||||||||||||||||||||||||||||||||
| Рис. 28 | Рис. 29 |
В полученной таблице вырежем ядро таблицы и назовём вырезанную таблицу матрицей смежности 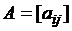 , где
, где 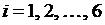 ,
, 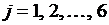 , для графа на рис. 28.
, для графа на рис. 28.
В математике прямоугольной матрицей называется совокупность чисел расположенных в виде прямоугольной таблицы, содержащей n строк и m столбцов. Такая матрица записывается в виде, показанном на рис. 30, или сокращенно в виде |
Граф, имеющий n вершин, ориентированный и неориентированный, можно представить массивом A, где A: array [1.. n, 1.. n ] of 0..1, и
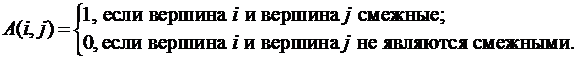
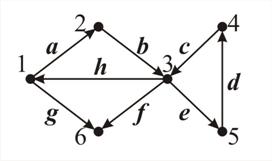
Для неориентированного графа (см. рис. 28), матрица смежности представлена на рис. 32. Матрица смежности для неориентированного графа является симметричной.
|
| Рис. 31 |
Представим матрицу смежности 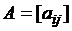 , где
, где 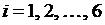 ,
, 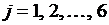 , для ориентированного графа (рис. 31). Элементы матрицы смежности выделены на рис. 33.
, для ориентированного графа (рис. 31). Элементы матрицы смежности выделены на рис. 33.
Основным преимуществом представления графа матрицей смежности является тот факт, что за один шаг можно получить ответ на вопрос, существует ли ребро из вершины U в V. Недостатком же является тот факт, что независимо от числа рёбер объём памяти для представления графа пропорционален 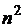 .
.

|
| |||||||||||||||||||||||||||||||||||||||||||||||||
| Рис. 32 | Рис. 33 |
Date: 2015-07-17; view: 886; Нарушение авторских прав




 ,
, 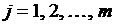 . Если число строк матрицы равночислу столбцов, то такая матрица называется квадратной. Квадратная матрица называется симметричной, если
. Если число строк матрицы равночислу столбцов, то такая матрица называется квадратной. Квадратная матрица называется симметричной, если 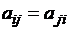 ,
,  [3].
[3].