
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Требования к уровню подготовки учащихся 7 page
|
|
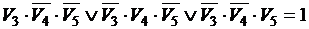 ,
, 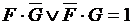 .
.
Получено пять тождественно истинных высказываний. Составим конъюнкцию этих высказываний. Получим логическую функцию
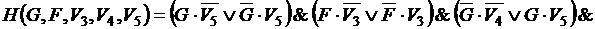
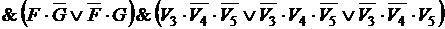 .
.
C. Упростим функцию H. Применим сначала закон коммутативности – второе и третье выражения в конъюнкции поменяем местами, а затем закон дистрибутивности конъюнкции относительно дизъюнкции к выражениям, определяющим функцию.
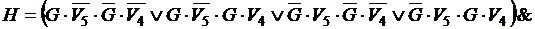
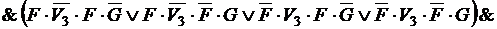
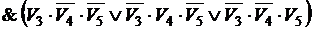 .
.
Преобразуем выражения в первой и второй скобках, учитывая, что 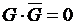 ,
, 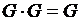 ,
, 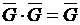 , получим:
, получим:
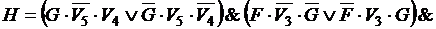
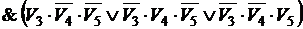 .
.
Применяя к выражениям, определяющим функцию, закон дистрибутивности конъюнкции относительно дизъюнкции и упрощая их, последовательно получаем:
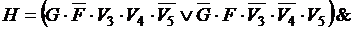
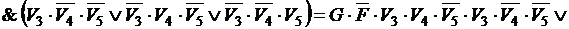
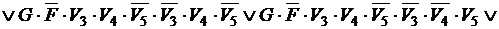
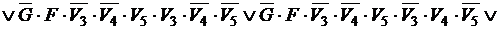
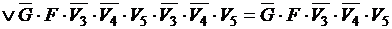 .
.
D. Определим, для какой совокупности значений пяти логических переменных G, F, V3, V4, V5 функция H принимает значение true. Дизъюнкция истинных высказываний есть истинное высказывание, следовательно, H =1, но  , отсюда
, отсюда 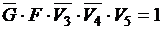 , а, следовательно, и
, а, следовательно, и 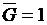 ,
, 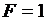 ,
, 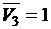 ,
, 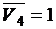 ,
, 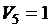 .
.
Таким образом, сосуд финикийский и изготовлен в V веке.
Программная реализация этапов C – D решения поставленной задачи
Сущность предлагаемого способа состоит в том, чтобы, выполнив этапы A и B, составить компьютерную модель процесса составления таблицы истинности для функции H и выбрать совокупности значений логических переменных G, F, 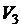 ,
, 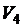 ,
, 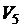 , при которых значение функции Н равно true. Выберем для компьютерной модели исполнителя Turbo Delphi.
, при которых значение функции Н равно true. Выберем для компьютерной модели исполнителя Turbo Delphi.
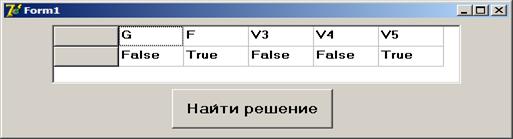
Оболочку программы можно взять из компьютерной модели на с. 106, изменив ядро программы, чтобы найти значения логических переменных G, F, V 3, V 4, V 5, при которых значение функции H истинно.
Результат выполнения программы
4.2. Применение графов к решению логических задач
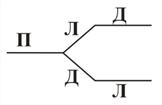
Задача. Из трех человек, стоящих рядом, один всегда говорит правду (правдивый), другой всегда лжет (лжец), а третий, смотря по обстоятельствам, говорит правду или ложь («дипломат»). У стоящего слева спросили: «Кто стоит рядом с тобой?» Он ответил: «Правдолюб». Стоящему в центре человеку, задали вопрос: «Кто ты?», и он ответил: «Я дипломат». Когда у стоящего справа человека, спросили: «Кто стоит рядом с тобой?», то он ответил: «Лжец». Кто, где стоял? Составьте информационную модель в виде графа и проведите исследования модели для нахождения решения.
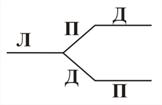
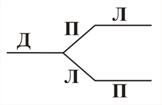
Решение. Если в данной задаче ребро графа будет соответствовать месту, занимаемому тем или иным человеком, то могут представиться следующие возможности их расположения (рис. 40).
| 
| 
|
| Рис. 40 |
Решение. Рассмотрим первую возможность. Если «правдолюб» стоит слева, то рядом с ним, судя по его ответу, также стоит «правдолюб». У нас же стоит лжец. Следовательно, эта расстановка не удовлетворяет условию задачи. Рассмотрев все остальные возможности, приходим к выводу, что расстановка «дипломат», «лжец», «правдолюб» удовлетворяет задаче. Действительно, если «правдолюб» стоит справа, то по его ответу, рядом с ним стоит «лжец», что выполняется. Стоящий в центре заявляет, что он «дипломат», и, следовательно, лжет. Таким образом, все условия задачи выполнены.
4.3. Табличные информационные модели решения логических содержательных задач
Задача. Беседуют трое друзей: Белокуров, Рыжов и Чернов. Брюнет сказал Белокурову: «Любопытно, что один из нас блондин, другой брюнет, третий — рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос у каждого из друзей?
Пояснение к решению. Для решения задачи можно предложить составить информационную модель в виде табл. 6. Интерпретируем следующее предложение: «Ни у кого из друзей цвет волос не соответствует фамилии». Поставим в соответствующих клетках символ «–». Между множеством фамилий участников беседы и множеством цветов волос должно быть установлено взаимно-однозначное соответствие. Если определили цвет волос у участника беседы, то в соответствующую клетку поставьте знак «+». В каждой ячейке таблицы должен быть поставлен один из знаков «+» или «–».
Таблица 6
| Фамилии | Цвет волос | ||
| рыжие | чёрные | русые | |
| Белокуров | – | ||
| Чернов | – | ||
| Рыжов | – |
5. Вопросы и задания к семинарским занятиям
Тема «Логические информационные и компьютерные модели»
Перефразируйте задания 1 – 6 главы 1, сформулировав предлагаемые задания и вопросы для рассматриваемой темы «Логические информационные и компьютерные модели». Выполните задания 1 – 6, ответьте на вопросы, поставленные в этих заданиях. Доложите результаты своей работы в студенческой аудитории в форме презентации.
7. Подберите мотивационные задачи для введения понятий, выделенных в составленной логико-структурной модели учебного материала по теме. Апробируйте свои разработки в студенческой аудитории.
8. Отберите содержание и разработайте методику изложения выбранного учебного материала по предложенным ниже темам. Проведите презентацию проделанной работы в студенческой аудитории:
8.1. Роль математической логики в информатике.
8.2. Высказывания. Логические константы. Логические переменные. Логические операции. Логические выражения, формулы, функции.
8.3. Упрощение сложных высказываний. Законы логики. Совершенная дизъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма. Карты Карно.
8.4. Программирование построения таблиц истинности логических функций.
8.5. Построение информационных и компьютерных моделей при решении логических содержательных задач.
8.6. Простейшие преобразователи информации. Построение информационных и компьютерных моделей для исследования логических функций.
8.7. Информационные и компьютерные модели типовых логических устройств компьютера.
9. На выбранной ступени непрерывного курса изучения информатики и информационно-коммуникационных технологий по темам пункта 8 смоделируйте серию последовательных уроков. Апробируйте в студенческой аудитории фрагмент одного из разработанных уроков.
10. Разработайте по выбранной схеме технологическую карту одного из уроков по выбранной теме содержательной линии «Моделирование и формализация». Проведите презентацию своей разработки в студенческой аудитории.
6. Лабораторно-практическая работа
Информационные и компьютерные модели, составленные при выполнении заданий 1, 2, представьте в студенческой аудитории в форме презентации.
Задание 1. Составьте информационные и компьютерные модели электронных логических устройств, выполняющих суммирование двоичных чисел: табличную модель, логическую функцию, функциональную схему, реализуйте информационные модели на соответствующем программном обеспечении:
а) одноразрядного полусумматора – устройства с двумя входами X и Y и двумя выходами Q и S;
б) одноразрядного сумматора – устройства с тремя входами X, Y, P и двумя выходами Q и S.
Примерный алгоритм решения задач а) и б):
· активизируйте правила сложения двоичных чисел;
· представьте правила сложения двоичных чисел в виде таблицы истинности (составьте табличную информационную модель работы сумматоров);
· используя СДНФ или СКНФ, составьте логические функции для нахождения Q и S (информационные модели работы сумматоров в виде логических функций от двух и трёх переменных соответственно), упростите полученные выражения;
· составьте функциональные схемы по соответствующим структурным формулам и компьютерные модели работы сумматоров для выбранных исполнителей (Ершол, QBasic, Turbo Pascal, Visual Basic.Net, Turbo Delphi, Microsoft Excel, Конструктор логических схем);
· проведите вычислительный эксперимент на выбранном программном обеспечении.
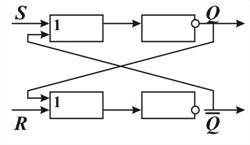
Задание 2. Составьте информационную модель работы асинхронного RS-триггера в виде таблицы истинности и исследуйте его работу с использованием компьютерной модели (рис. 41).
|
| Рис. 41 |
Задание 3. Разработайте и реализуйте с использованием выбранного исполнителя учебный проект в виде компьютерной модели на тему «Конструктор логических схем», рассмотрите при проектировании все этапы составления компьютерных моделей. Подготовьте проект к защите.
Задание 4. Составьте с использованием электронных таблиц и систем программирования компьютерные модели для решения отобранных вами логических содержательных задач. Результаты выполнения задания оформите в виде презентации и защитите в студенческой аудитории.
Задание 5. Составьте логические содержательные задачи, для решения которых необходимо использовать компьютерные модели, моделирующие процесс поиска решения задач. Разработайте методику обучения школьников поиску решения предложенных задач, оформите решения составленных задач. Апробируйте разработанные методики в студенческой аудитории.
7. Самостоятельная работа
Выполнение заданий 1 – 4 и задач 1 – 2 подготовьте для проверки при индивидуальном собеседовании.
Задание 1. Логическая функция 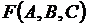 задана таблицей значений, определите выражение этой функции через логические операции Ø, Ù,Ú, используя СДНФ и СКНФ. Упростите полученное выражение с использованием законов логики и карт Карно:
задана таблицей значений, определите выражение этой функции через логические операции Ø, Ù,Ú, используя СДНФ и СКНФ. Упростите полученное выражение с использованием законов логики и карт Карно:
а)
| A | ||||||||
| B | ||||||||
| C | ||||||||
| F |
б)
| A | ||||||||
| B | ||||||||
| C | ||||||||
| F |
Задание 2. Упростите заданные логические функции F. Упрощённый вид этих функций должен содержать не более трёх логических операций. Составьте для упрощённых функций F функциональные схемы:
а) 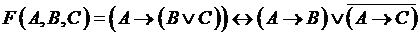 ,
,
б) 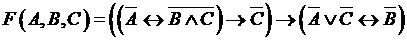 .
.
Задание 3. Составьте логическое выражение, реализуемое приведенной ниже функциональной схемой. Вычислите значение логического выражения при 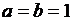 ;
;  ;
; 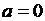 ,
, 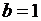 . Упростите полученное логическое выражение. Составьте функциональную схему, соответствующую упрощенному выражению (рис. 42).
. Упростите полученное логическое выражение. Составьте функциональную схему, соответствующую упрощенному выражению (рис. 42).
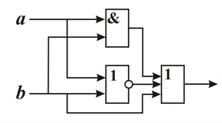
|
| Рис. 42 |
Задание 4. Разработайте сценарии программ (демонстрационных, обучающих, тренажеров, контролирующих) по данной теме и реализуйте их на одном из языков программирования.
Задача 1. В некотором университете проходит в несколько туров конкурс вокала. Тремя членами жюри (A, B, C) решается вопрос о допуске того или иного участника к следующему туру. Решение положительно тогда и только тогда, когда большинство членов жюри высказывается за допуск. Разработайте компьютерную модель для голосования и реализуйте её с использованием соответствующего программного обеспечения.
Задача 2. Решите поставленную задачу, составив информационную модель с помощью кругов Эйлера – Венна. В школе из 100 учеников английский язык изучают 28, немецкий – 30, французский – 42, английский и немецкий – 8, английский и французский – 10, немецкий и французский – 5, немецкий, английский и французский – 3. Сколько учеников не изучают ни одного языка? Сколько человек изучают только немецкий язык, только английский язык, только французский?
Пояснение к решению задачи
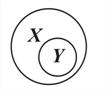
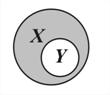
Нужно использовать наглядную геометрическую иллюстрацию объёмов понятий и отношений между ними, выделив следующие виды отношений: пересечение, включение, дополнение (рис. 43).
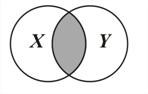
| 
| 
|
Пересечение 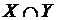
| Включение 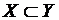
| Дополнение 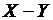
|
| Рис. 43 |
Приложение
Примеры учебных[9] компьютерных моделей процессов,
реализованных в решении практических задач
Приложение 1. Компьютерные модели процесса нахождения эйлерового цикла в графе
В приложении 1 даны компьютерные модели нахождения эйлерова цикла в графе, для которого выполняются необходимые и достаточные условия существования этого цикла (см. с. 80). Для того чтобы использовать модели для определения существования эйлерова пути (определения, является ли диаграмма исследуемого графа уникурсальной линией), необходимо дополнить модели процедурами с учётом замечания 1.
Алгоритм нахождения эйлерова цикла
Для реализации процесса нахождения эйлерового цикла от выбранной вершины организуйте два стека: стек ST и ST1. Так как стеки в предложенных моделях организованы в виде массивов, то необходимо выбрать два указателя uk и uk1, типа byte, на соответствующие вершины стеков.
1. Введите в память компьютера матрицу смежности A либо с клавиатуры, либо с использованием типизированной константы-массива, либо из текстового файла.
2. Введите начальную вершину эйлерового цикла – V. Поместите её в стек ST.
3. Пока стек ST не пуст, выполняйте шаги 4, 4.1, 4.2, иначе идите на шаг 5.
4. Просматривайте граф «в глубину», начиная от вершины графа T, находящейся в вершине стека ST:
4.1. Если найдена вершина J, смежная с рассматриваемой вершиной T, то поместите её в стек ST и удалите рёбро { T, J } из графа, т.е. соответствующим элементам матрицы смежности A присвойте значение нуль: a[t,j]:=0, a[j,t]:=0, и идите на шаг 3, иначе идите на шаг 4.2.
4.2. Если нет в преобразованном графе вершин J, смежных с вершиной T, находящейся в вершине стека ST, то вершину T поместите в стек ST 1, а из стека ST удалите вершину T, и идите на шаг 3. В этом случае из графа был удалён цикл, и вершины этого цикла находятся в стеке ST.
5. Выведите на экран или в файл вершины из стека ST 1, определяющие эйлеров цикл, начиная с выбранной вами вершины. Закончите исполнение алгоритма.
Компьютерная модель 1 процесса нахождения эйлерового цикла [10]. Компьютерная модель реализована в системе Turbo Pascal. Граф задаётся матрицей смежности, элементы которой вводятся из текстового файла. Полное имя текстового файла и номер начальной вершины цикла нужно ввести с клавиатуры в процессе работы программы.
Program cycle; { Поиск Эйлерова цикла }
uses Crt;
const n = 7; m = 12; k=14;
type mass = array [1..n, 1..n] of byte;
type mass1 = array [1..k] of byte;
{ если система Turbo Pascal позволяет использовать
типизированные константы, то для отладки программы
можно этим воспользоваться:
const
a:mass = ((0,1,0,0,1,0,0),(1,0,1,0,1,1,0),
(0,1,0,1,0,1,1), (0,0,1,0,1,1,1), (1,1,0,1,0,1,0), (0,1,1,1,1,0,0), (0,0,1,1,0,0,0));}
var
t,v,j,uk,uk1,uk2,i,j1:byte;a:mass;
st1,st,st2: mass1; pr: boolean;
Procedure input;
Var
f: text; i,j,b: byte; name: string [20];
Begin
write ('введите имя текстового файла,');
write ('содержащего элементы матрицы смежности'); readln (name);
assign (f,name);
reset (f);
for i:=1 to n do
for j:=1 to n do
begin
read(f,b); { чтение числа b из файла в ОЗУ}
a[i,j]:=b; {присвоение текущему элементу матрицы смежности значение b}
end;
close (f);
end;
Procedure print1 (x1:mass1; uk2:byte);
{процедура печати элемента стека, определяемого именем X1}
var apex:byte;uk3:byte;x2:mass1;
begin
uk3:=0;
while uk2<>0 do
begin
apex:=x1[uk2]; uk2:=uk2-1; uk3:=uk3+1; x2[uk3]:=apex;
end;
while uk3>0 do
begin write (x2[uk3], ';'); uk3:=uk3-1; end;
writeln;
end;
begin {основная программа}
clrscr; input; {ввод матрицы смежности};
write('введите первую вершину для просмотра'); readln(v);
uk1:=0; uk:=1; st [uk]:=v; {инициализация стека ST}
while (uk <> 0) do {обход графа «в глубину» с удалением просмотренных рёбер}
begin
t:=st[uk]; j:=1; pr:=false;
repeat
if a[t,j]<>0 then
pr:=true
else
j:=j+1
until (pr) or (j>n);
{найдено новое ребро или все ребра инцидентные с вершиной V просмотрены}
{обработка поиска}
If pr then
begin
uk:=uk+1; st[uk]:=j; a[t,j]:=0; a[j,t]:=0; Write('стек st: ');print1(st,uk);
end
else
begin
uk1:=uk1+1; st1[uk1]:=t; Write('стек st1: ');print1(st1,uk1); uk:=uk-1
end
end;
writeLn('**************************************');
writeLn ('Эйлеров цикл от вершины ', v); print1(st1,uk1);
writeLn('**************************************')
End.
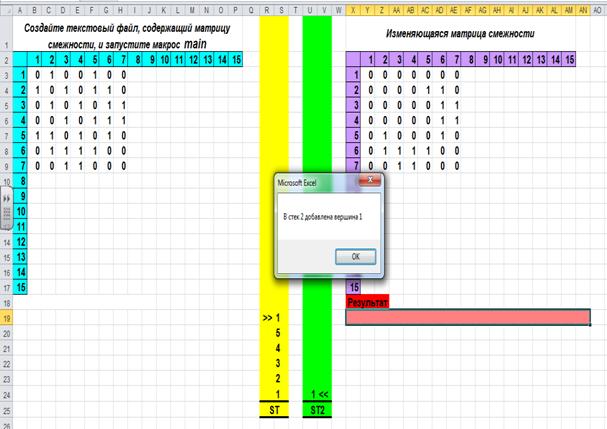
Компьютерная модель 2 процесса нахождения эйлерового цикла. Компьютерная модель реализована в электронных таблицах MS Office Excel с использованием языка VBA. Матрица смежности вводится из текстового файла, полное имя которого вы должны ввести с клавиатуры и ввести номер начальной вершины цикла.
Dim n, fn As Integer, uk1, uk, a(15, 15), st(15), st1(15), st2(15) As Byte
Sub main()
n = InputBox("введите количество вершин графа")
vvod
unikurs
End Sub
Sub vvod()
'очистка
Range("B3:P15").Select: Selection.ClearContents
Range("Y3:AM15").Select: Selection.ClearContents
Range("R1:V24").Select: Selection.ClearContents
Range("X19:AN19").Select: Selection.ClearContents
'ввод матрицы смежности
fn = FreeFile: s = InputBox("Введите полный путь к файлу ")
Open s For Input As fn
For i = 1 To n
For j = 1 To n
c = Input(1, fn)
If (c <> "0") And (c <> "1") Then j = j - 1: GoTo 1
Cells(i + 2, j + 1).Value = c
a(i, j) = Cells(i + 2, j + 1).Value
1: Next j
Next i
Close fn
For i = 1 To n
For j = 1 To n
Cells(i + 2, j + 24).Value = a(i, j)
Next j, i
End Sub
Sub unikurs()
v = InputBox("Введите первую вершину для просмотра")
'инициализация стека st
uk1 = 0: uk = 1: st(uk) = v
Cells(25 - uk, 19).Value = st(uk)
'просмотр в глубину
While uk <> 0
t = st(uk): j = 1: pr = False
Do
If a(t, j) <> 0 Then pr = True Else j = j + 1
Loop Until (pr) Or (j > n)
'найдено новое ребро или все ребра, инцидентные с вершиной v, просмотрены
'обработка поиска
If pr Then
uk = uk + 1: st(uk) = j
a(t, j) = 0: Cells(t + 2, j + 24).Value = 0: a(j, t) = 0: Cells(j + 2, t + 24) = 0
Cells(25 - uk, 19).Value = st(uk): Cells(25 - uk, 18).Value = ">>"
Cells(25 - uk + 1, 18).Value = ""
For q = 1 To 20000000
Next q
Else
uk1 = uk1 + 1: st1(uk1) = t: Cells(25 - uk1, 21).Value = st1(uk1)
Cells(25 - uk1, 22).Value = "<<": Cells(25 - uk1 + 1, 22).Value = ""
MsgBox ("В стек 2 добавлена вершина " & st1(uk1))
For q = 1 To 20000000
Next q
uk = uk - 1
End If
Wend
print1 (uk1) 'печать результата
End Sub
Sub print1(uk As Byte)
'процедура вывода на экран маршрута обхода графа,
'удовлетворяющего требуемому условию
Dim uk2 As Byte
uk2 = 0
While uk <> 0
apex = st1(uk): uk = uk - 1: uk2 = uk2 + 1: st2(uk2) = apex
Wend
i = 1
While uk2 > 0
Cells(19, i + 23).Value = st2(uk2): uk2 = uk2 - 1: i = i + 1
Wend
End Sub
Вид окна MS Excel в промежуточный момент исполнения программы
Замечание 1. Чтобы использовать модели для определения существования эйлерова пути в графе G (определения, является ли диаграмма исследуемого графа уникурсальной линией), необходимо дополнить модели процедурами:
1. Процедурой определения степени вершин графа G, используя для нахождения степеней вершин графа, например, матрицу смежности. Если вершин с нечётной степенью в графе G больше, чем две, то выдайте ответ, что не существует в графе G эйлерова пути, диаграмма графа G не является уникурсальной линией.
2. Процедурой определения связности графа G, используя для проверки связности графа G, например, матрицу достижимости. Если граф G несвязный, то выдайте ответ, что не существует в графе G эйлерова пути, диаграмма графа не является уникурсальной линией.
3. Если есть не более двух вершин нечётной степени у исследуемого связного графа G, например, вершины U и V, то образуйте граф  [11]:
[11]:
а) Добавьте в граф G новое ребро { U, V }, если { U, V } не принадлежит графу G.
б) Дополните граф G новой вершиной R и рёбрами { U, R } и { R, V }, если ребро { U, V } принадлежит графу G.
в) Воспользуйтесь предложенными моделями для нахождения эйлерова цикла в графе  , начиная от вершины или U, или T, или V.
, начиная от вершины или U, или T, или V.
г) В полученном эйлеровом цикле уберите добавленные рёбра. Получите эйлеров путь, который начинается либо от вершины U, либо от вершины V.
Прил. 2. Компьютерные модели «Электронный кассир», имитирующие работу кассира по продаже билетов в кинотеатр на один сеанс
Компьютерная модель 1 «Электронный кассир», реализованная в системе QBasic. Пример разработки алгоритма и реализации некоторых процедур программы описаны на с. 23.
REM Casier:
DECLARE SUB delay1 ()
DECLARE SUB clrscr1 (): DECLARE SUB Write2 ()
DECLARE SUB clrscr2 ()
DECLARE SUB delay (): DECLARE SUB Sale (): DECLARE SUB Selection ()
Основная программа
DIM SHARED o AS INTEGER: DIM SHARED time2 AS LONG
DIM SHARED TIME1 AS LONG: DIM SHARED time3 AS LONG
DIM t AS INTEGER: DIM SHARED f AS INTEGER
DIM SHARED fl1 AS INTEGER: DIM SHARED I AS INTEGER
DIM SHARED j AS INTEGER: DIM SHARED r AS INTEGER
DIM SHARED m AS INTEGER: DIM SHARED n AS INTEGER
DIM SHARED n1 AS INTEGER: DIM SHARED sum AS INTEGER
DIM SHARED z AS INTEGER
r = 5: m = 7: f = 1
DIM SHARED card(r, m + 1) AS INTEGER
DIM SHARED cost(r) AS INTEGER
RANDOMIZE TIMER
CLS
sum = 0 'sum-количество проданных билетов
'формирование массива card
FOR I = 1 TO r
FOR j = 1 TO m
card(I, j) = INT(RND * 2)
IF card(I, j) = 1 THEN sum = sum + 1
NEXT j
card(I, m + 1) = 1
NEXT I
'формирование массива cost
'цена билетов по рядам
t = INT(RND * 100)
cost(1) = t: cost(2) = t: cost(r - 1) = t: cost(r) = t: t = INT(RND * 200)
FOR I = 3 TO r - 2
cost(I) = t + I * 10
NEXT I
'вывод расположения мест и цены билетов
Write2
time2 = TIMER
TIME1 = 0
'организация диалога покупателей и кассира
WHILE (sum < r * m) AND (TIME1 <= 300)
o = 0
LOCATE 11, 10: PRINT "Диалог с "; f; " покупателем:"
LOCATE 12, 10: INPUT "Хотите купить билеты?(1-да,2-нет)"; o1
IF o1 = 1 THEN
LOCATE 13, 10: INPUT "Сколько билетов Вам нужно?"; n
IF n > 0 THEN Sale
END IF
'анализ диалога с покупателем
f = f + 1
time3 = TIMER
time1 = time3 - time2
IF o1 <> 1 THEN
LOCATE 22, 3: PRINT "Не хотите покупать билеты! До свидания!"
GOTO 6
END IF
IF o = 1 THEN Write2
IF o = 2 THEN
LOCATE 22, 3: PRINT "К сожалению, других свободных мест нет! Извините! До свидания!"
END IF
IF fl1 = 0 THEN
LOCATE 22, 3: PRINT "К сожалению, вместе расположенных"; n; " мест нет"
END IF
6: delay
clrscr2
Date: 2015-07-17; view: 612; Нарушение авторских прав