Задание 4.3

Методом аппроксимации блочно-импульсными функциями нулевого порядка и локально-импульсными функциями первого порядка выполнить аппроксимацию сигнала 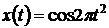на интервале [0,1], .

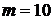Сгенерируем блочно-импульсные базисные функции нулевого порядка в соответствии с формулами (4.5), (4.6). Отрезок [0,1] разобьем на 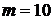частей длиной 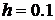и для каждого 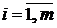вычислим 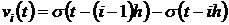. Для этого оформим функцию единичного скачка 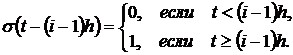и .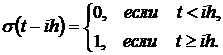

Для проверки условия на каждом частичном промежутке оформим блок Constant, содержащий значения 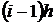при 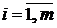, то есть постоянную 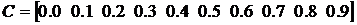зададим в виде вектора с соответствующими компонентами или, что то же самое 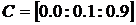(рис. 4.21), а блок Constant1, содержащий значения 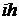при 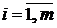, зададим в виде диапазона значений .

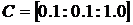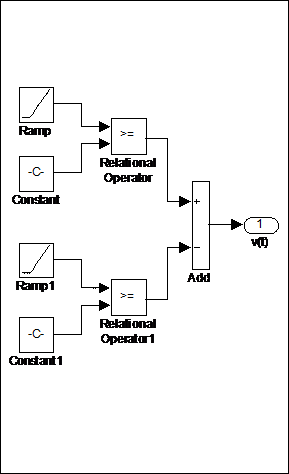
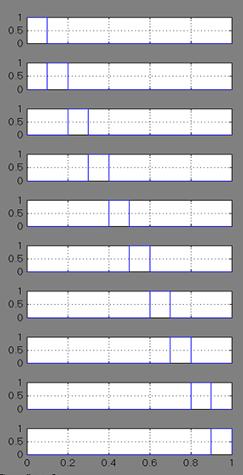
Рис. 4.21 Структурная схема, генерирующая блочно-импульсные функции нулевого порядка и графики блочно-импульсных функций

Рядом со схемой на рис. 4.21 показан вид блочно-импульсных функций нулевого порядка, образующих базис, при этом каждая из функций имеет столбик единичной высоты на соответствующем частичном промежутке.

В соответствии с формулами (4.8) построим систему локально-импульсных базисных функций первого порядка. При этом в блоке Constant1 (рис. 4.22) задаются значения 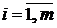в виде вектора 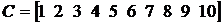или, что то же самое .

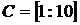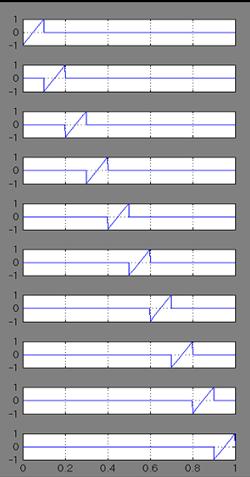
Рис. 4.22 Структурная схема, генерирующая локально-импульсные функции первого порядка и графики кусочно-линейных функций

Структурная схема анализа сигнала рассматриваемым методом представлена на рис. 4.23. Назначение блоков следующее:

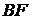- генерирует систему базисных функций;

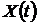- генерирует анализируемый сигнал;

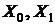- рассчитывают элементы спектра по формулам метода наименьших квадратов;

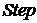- определяет момент записи спектра в рабочую область.

Полученный спектр, кроме записи в рабочую область, можно выдать на дисплей.

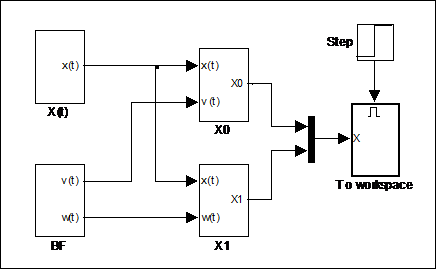
Рис. 4.23 Структурная схема анализа сигнала блочно-импульсным методом

Структурная схема, представленная на рис. 4.24, восстанавливает сигнал. На вход схемы подаются базисные функции и спектр анализируемого сигнала, на выход – аппроксимация сигнала по соответствующему методу и исходный сигнал.

На виртуальный осциллограф подаются исходный и восстановленный сигналы. Они представлены на рис. 4.25 для обоих методов соответственно. Из графиков видно, что даже при небольшом числе подинтервалов (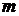) получается довольно точная аппроксимация сигнала. Точность можно повышать, разбивая интервал определения сигнала на большее количество подинтервалов.

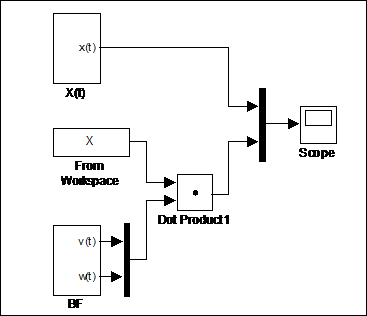
Рис. 4.24 Структурная схема синтеза сигнала

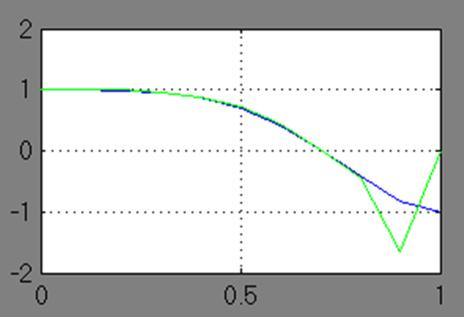
Рис. 4.25 Результаты аппроксимации сигнала

Варианты для выполнения Задания 4.3

Методом аппроксимации блочно-импульсными функциями нулевого и первого порядков выполнить аппроксимацию сигнала на интервале [0,1], 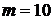из лабораторной работы №1 в соответствие со своим вариантом.

Date: 2015-07-17; view: 474; Нарушение авторских прав