Задание 4.2

Модифицированным методом равных площадей аппроксимировать тот же сигнал 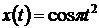на интервале [0,1]. В качестве базисных функций взять те же степенные функции до 4-го порядка включительно.

Модель аппроксимации сигнала модифицированным методом равных площадей можно строить в соответствие с теми же этапами, что и модель в задании 4.1, а окончательную модель оформить как совокупность выполняемых подсистем.

Для упрощения построений можно воспользоваться результатами выполнения задания 4.1 и лишь преобразовать необходимые подсистемы. Эти преобразования связаны с тем, что в соответствии с методом равных площадей интервал изменения аргумента разбивается, например, на пять подинтервалов [0; 0,2], [0,2; 0,4], [0,4; 0,6], [0,6; 0,8], [0,8; 1,0] и на каждом из них строится система коэффициентов аппроксимирующего спектра по формулам (4.4), (4.2).

Первый этап. Подсистема построения сигнала 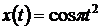на интервале [0,1] может быть взята из задания 4.1 (рис. 4.4).

Второй этап. Подсистема построения базисных функций 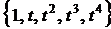соответствует заданию 4.1 (рис. 4.14).

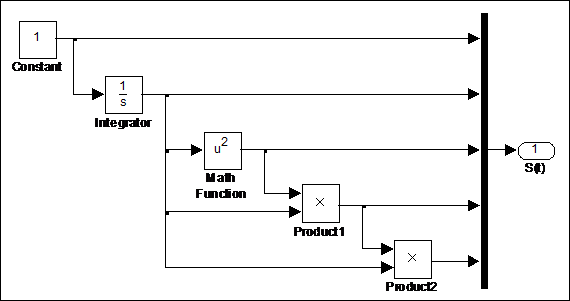
Рис. 4.14 Подсистема построения базисных функций

Третий этап. А вот подсистема построения вектора аппроксимирующего спектра Subsystem2 будет подвергнута значительным изменениям.

Исходя из формул (4.4), можно заметить, что как при расчете вектора 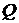, так и при расчете векторов-столбцов матрицы 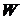общим является интегрирование функции на одних и тех же интервалах. Таким образом, для получения вектора 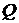необходимо проинтегрировать на заданной системе подинтервалов сигнал 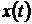, а для получения столбцов матрицы 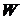необходимо проинтегрировать базисные функции на той же системе подинтервалов. Это позволяет для выполнения указанных операций использовать одну и ту же подсистему, структурная схема которой представлена на рис. 4.15.

Рис. 4.15 Блок интегрирования функции на системе подинтервалов

На вход этого блока поступает сигнал – интегрируемая функция. Два других сигнала – нулевой и генератор линейно возрастающей функции времени являются вспомогательными. Пока время находится в пределах заданного подинтервала, переключатель Switch подает на интегратор сигнал 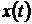. Но как только время выходит за пределы подинтервала, сигнал переключается на нулевой и больше не влияет на значение интеграла.

Так как MatLab ориентирован в основном на обработку массивов данных, то имеет смысл задавать в параметрах блоку Switch не один подинтервал, а вектор, состоящий из всех пяти подинтервалов, тогда на выходе также получим вектор значений интеграла. Определение системы подинтервалов с помощью параметров блока Switch показано на рис. 4.16.

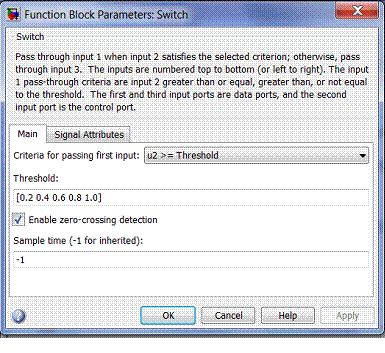
Рис. 4.16 Окно настройки параметров блока Switch

Теперь рассмотрим структурную схему блока Subsystem2, представленную на рис. 4.17.

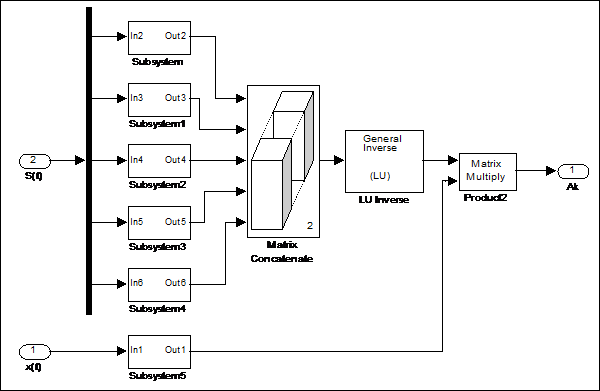
Рис. 4.17 Подсистема построения аппроксимирующего спектра

На вход блока подается сигнал 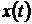и система базисных функций 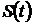. Подсистема Subsystem5 интегрирует сигнал и подает на выход вектор 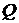, а подсистемы Subsystem – Subsystem4 интегрируют векторы-столбцы матрицы .

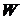Блок Matrix Concatenate объединяет столбцы в матрицу. Далее размещены блоки расчета обратной матрицы и умножения матриц. На выходе получаем сигнал аппроксимирующего спектра, который появляется на экране дисплея модели верхнего уровня (рис. 4.18).

Четвертый этап. Рассмотрим задачу построения сигнала по заданному спектру в системе базисных функций. Для наглядности используем спектр, полученный выше, на основе его построим аппроксимацию и сравним ее с реальным сигналом.

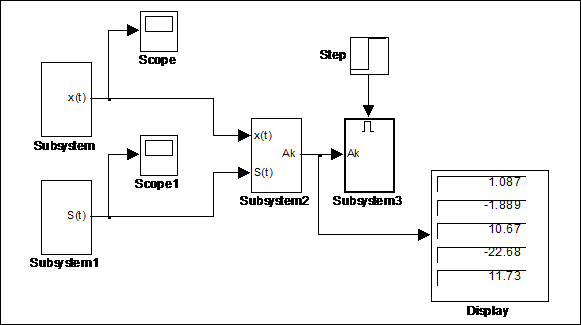
Рис. 4.18 Модель построения аппроксимирующего спектра с результатами

Структурная схема получения сигнала, как и в задании 4.1, будет иметь вид, показанный на рис. 4.19. Блок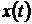и и 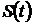были описаны ранее. Блок From Workspace извлекает из рабочей области спектр сигнала. Базисные функции умножаются на соответствующие коэффициенты спектра, суммируются и выводятся на виртуальный осциллограф. На этот же осциллограф подается первоначальный сигнал. Графики сигнала и его аппроксимации, представленные на рис. 4.20, практически совпадают.

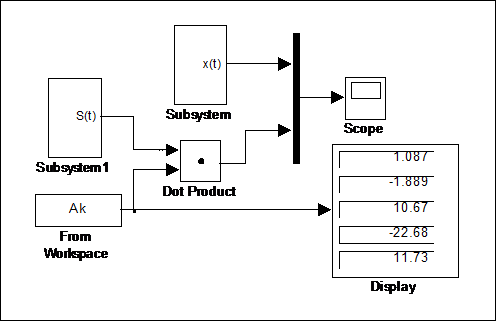
Рис. 4.19 Структурная схема получения аппроксимирующего сигнала

Рис. 4.20 График заданного сигнала и его аппроксимация

Рассмотренные модели применяются для решения большого количества задач, связанных с цифровой обработкой сигналов, в том числе с обработкой звуковых сигналов и изображений.

Варианты для выполнения Задания 4.2

Модифицированным методом равных площадей на интервале [0,1] аппроксимировать сигнал из лабораторной работы №1 в соответствие со своим вариантом. В качестве базисных функций взять степенные функции вида 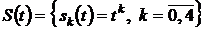, то есть систему 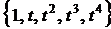. Систему подинтервалов оставить как в примере.

Date: 2015-07-17; view: 439; Нарушение авторских прав