Аппроксимация непрерывных и дискретных сигналов

При решении многих прикладных задач используются методы приближения довольно сложных для исследования функций более простыми, хорошо изученными функциями (например, многочленами). При этом исследуемая функция может быть задана как в аналитическом, так и дискретном виде (в виде экспериментальной таблицы большой размерности). Процедура замены заданной функции другой, более простой, функцией называется аппроксимацией. На практике такие задачи возникают, например, при преобразовании аналогового сигнала в цифровой и, наоборот, из цифрового сигнала в аналоговый.

Сформулируем задачу аппроксимации. Пусть непрерывная (дискретная) функция 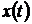задана на некотором интервале изменения аргумента 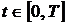. Требуется заменить эту функцию некоторой простой, но хорошо исследуемой функцией, сохранив поведение функции на указанном промежутке.

Для решения поставленной задачи выбирается некоторая система базисных функций 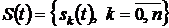, заданных на том же интервале изменения аргумента. При этом заданная функция представляется некоторым обобщенным многочленом в виде разложения по базисным функциям

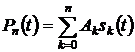, (4.1)

где коэффициенты 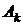подлежат определению, при этом систему коэффициентов 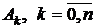обычно называют аппроксимирующим полиномиальным спектром (АПС) сигнала .

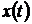Решение задачи можно представить в виде структурной схемы модели верхнего уровня в виде последовательности двух блоков (рис. 4.1). Входными сигналами первого блока являются заданная функция 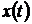и выбранная система базисных функций 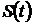. Аппроксимирующий спектр 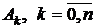, являющийся выходом из первого блока, подается на вход второго блока для построения аппроксимирующей функции .

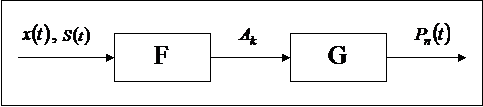
Рис. 4.1 Структурная схема аппроксимации функций

Для нахождения аппроксимирующего спектра 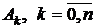, а следовательно и самой функции , рассмотрим два метода: метод наименьших квадратов и модифицированный метод равных площадей. В частности, для анализа дискретных динамических систем удобнее использовать метод равных площадей.

Date: 2015-07-17; view: 531; Нарушение авторских прав