Модифицированный метод равных площадей

Метод равных площадей является более простым методом аппроксимации, основанный на определении коэффициентов аппроксимирующего многочлена (4.1), исходя из условия равенства нулю интегралов функций ошибки аппроксимации на некоторой системе интервалов изменения аргумента.

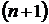Суть модифицированного метода равных площадей заключается в следующем. Интервал изменения аргумента разбивается на часть (систему подинтервалов). Уравнение аппроксимирующей кривой подбирается так, чтобы площади, ограничиваемые заданной и аппроксимирующей функциями, были равны между собой для каждого участка в отдельности. Это приводит к системе линейных алгебраических уравнений, решение которой определяет аппроксимирующий спектр.

Условия равенства указанных площадей (интегралов) для некоторой системы линейно-независимых подинтервалов имеет вид:

.

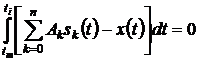Например, при выборе системы подинтервалов вида 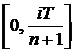, , 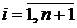матрица 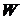и вектор 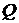вычисляются по формулам:

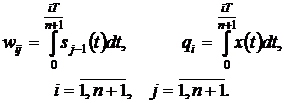(4.4)

Вектор аппроксимирующего спектра 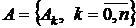определяется по формуле (4.2), сама же аппроксимирующая функция по формуле (4.1).

Date: 2015-07-17; view: 695; Нарушение авторских прав