Задание 4.1

Методом наименьших квадратов аппроксимировать сигнал 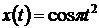на интервале [0,1]. В качестве базисных функций взять степенные функции до 4-го порядка включительно.

Выполнение поставленной задачи разобьем на несколько этапов.

1. Сгенерируем непрерывный сигнал 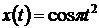на интервале [0,1].

2. Сгенерируем систему степенных функций .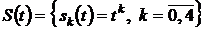

3. Определим вектор аппроксимирующего спектра 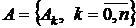по формулам (4.3), (4.2).

4. Сгенерируем аппроксимирующий многочлен .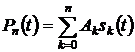

Первый этап. Модель получения непрерывного сигнала 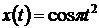на интервале [0,1] формируется известным по лабораторной работе №1 способом, результат представлен на рис. 4.3.

Рис. 4.3 Фрагмент модели построения сигнала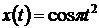

Однако, для того чтобы итоговая модель не была слишком громоздкой, отдельные этапы построения модели будем оформлять в виде подсистем, из которых и будет окончательно состоять модель.

Построенный фрагмент модели оформим как подсистему, для этого выделим все блоки, генерирующие сигнал 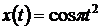, кроме блока Scope, и выполним команду Create Subsystem из меню Edit окна модели. Выделенный фрагмент будет помещен в подсистему, а вместо него в основном окне модели появится блок Subsystem.

Двойной щелчок по блоку Subsystem откроет дополнительное окно подсистемы, в котором отобразится спрятанный фрагмент, при этом выход подсистемы будет снабжен соответствующим выходным портом out1, который можно переименовать в x(t).

Результат преобразований показан на рис. 4.4.

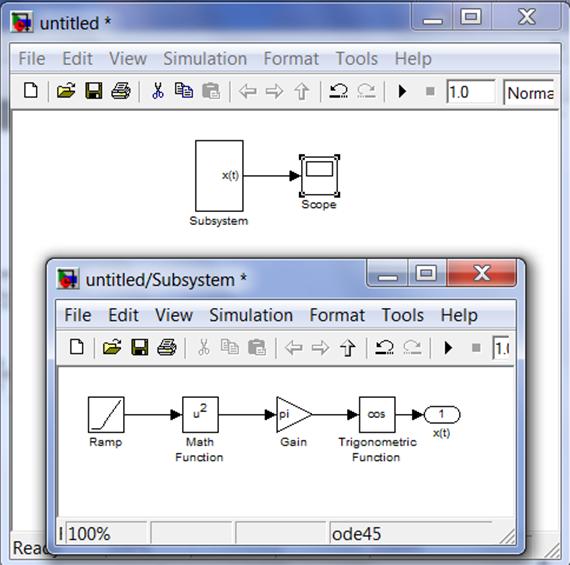
Рис. 4.4 Результат преобразования фрагмента системы в подсистему

Второй этап. Аналогичным образом поступим при построении системы базисных степенных функций 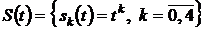. Сначала в основном окне построим структурную схему вычисления функций 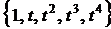и преобразуем их в вектор при помощи блока Mux (рис. 4.5), затем выделим соответствующий фрагмент схемы и преобразуем его в подсистему описанным выше способом.

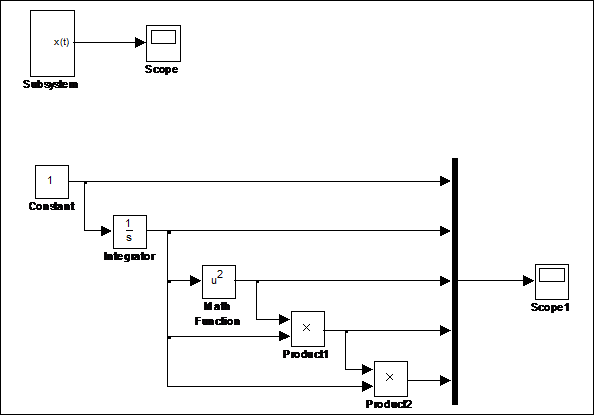
Рис. 4.5 Построение системы базисных функций

Модель в основном окне примет вид, показанный на рис. 4.6.

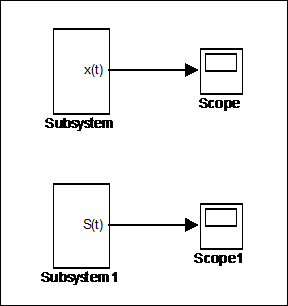
Рис. 4.6 Фрагмент модели, состоящий из подсистем

Третий этап. Определим вектор аппроксимирующего спектра 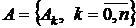по формулам (4.3), (4.2). Вычисления коэффициентов можно сформировать при помощи схемы, показанной на рис. 4.7.

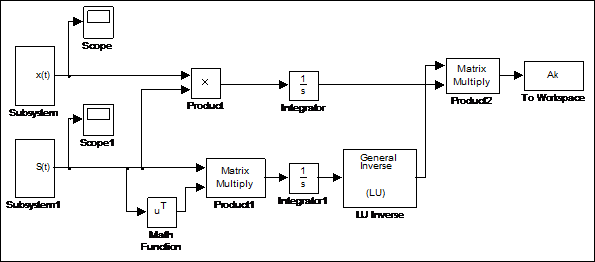
Рис. 4.7 Структурная схема определения коэффициентов аппроксимирующего многочлена

Здесь элементы 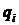вектора 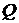получаются при умножении компонент вектора 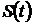на сигнал 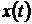с последующим интегрированием. Элементы 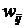матрицы 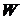получаются при умножении вектора-строки 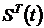на вектор-столбец 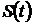с последующим интегрированием. Для получения обратной матрицы 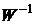используется блок LU Inverse. Аппроксимирующий спектр 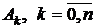получается, в соответствие с формулой (4.2), умножением матриц 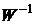и 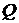. Описанные вычисления преобразуем в подсистему, изображенную на рис. 4.8.

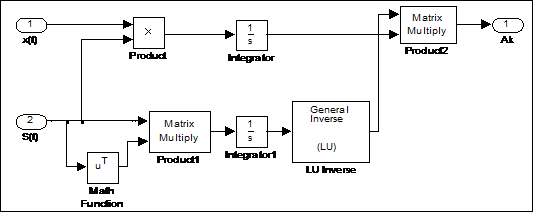
Рис. 4.8 Подсистема определения коэффициентов спектра

Модель в основном окне примет вид, показанный на рис. 4.9.

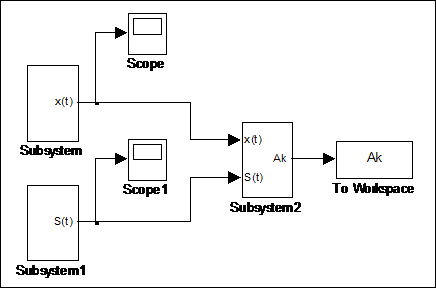
Рис. 4.9 Основная модель с тремя подсистемами

Осталось доработать блок To Workspace, используемый для записи результатов в рабочую область программы Matlab. На промежутке [0,1] аппроксимирующий спектр 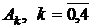генерируется в каждый момент времени 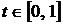c некоторым варьируемым шагом. Для этого работой блока To Workspace необходимо управлять с помощью блока Step, генерирующего ступенчатый сигнал.

Преобразуем блок To Workspace в подсистему (рис. 4.10), в которую добавим блок Enable, при помощи которого можно управлять записью результатов в рабочую область. А самому блоку To Workspace зададим свойству Save format значение Structure With Time.

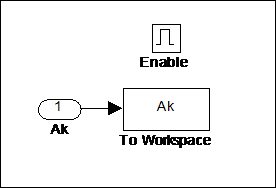
Рис. 4.10 Подсистема сохранения результатов расчета аппроксимирующего спектра в рабочую область

Окончательный вид основной модели с результатами моделирования на последнем шаге показан на рис. 4.11.

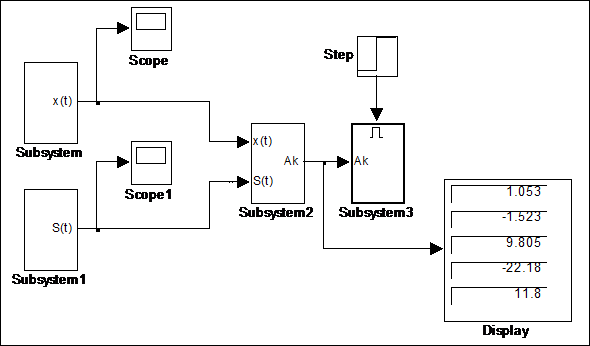
Рис. 4.11 Окончательный вид модели расчета коэффициентов по методу наименьших квадратов

Четвертый этап. После расчета коэффициентов аппроксимирующего спектра искомый аппроксимирующий сигнал восстанавливается по схеме, приведенной на рис. 4.12.

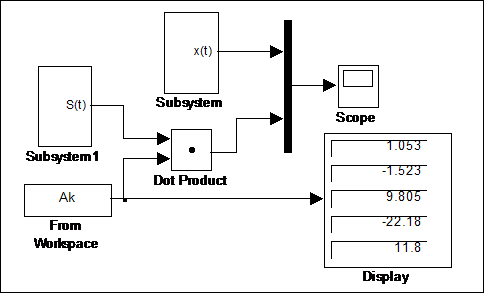
Рис. 4.12 Восстановление сигнала по найденному спектру

Результаты работы модели выводятся на экран виртуального осциллографа, при этом на рис. 4.13 слева показан исходный сигнал, а справа изображены исходный и наложившийся на него аппроксимирующий сигнал.

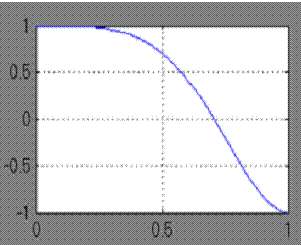
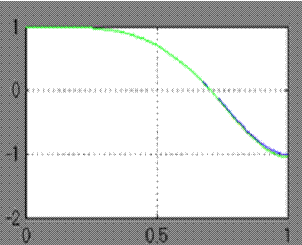
Рис. 4.13 Исходный сигнал 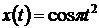и его аппроксимация по методу наименьших квадратов

Варианты для выполнения Задания 4.1

Методом наименьших квадратов на интервале [0,1] аппроксимировать сигнал из лабораторной работы №1 в соответствие со своим вариантом. В качестве базисных функций взять степенные функции вида 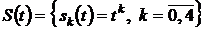, то есть систему .

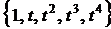Date: 2015-07-17; view: 504; Нарушение авторских прав