Задание 2.1

Пример 1. Найти решение системы алгебраических уравнений:

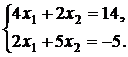
Система является системой с преобладающими диагональными элементами 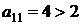, , поэтому для ее решения применим метод сведения ее к эквивалентной системе дифференциальных уравнений

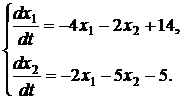
Структурная схема модели данной системы приведена на рис. 2.2.

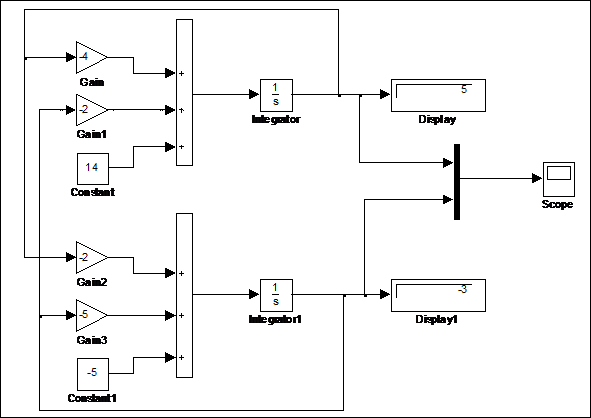
Рис.2.2 Структурная схема модели системы дифференциальных уравнений

Схема построена с использованием классических методов аналоговой вычислительной техники. Входными сигналами схемы являются значения 14 и – 5, при этом на входы интеграторов Integrator и Integrator1 подаются сформированные правые части первого и второго уравнения, а на выходах получаются значения искомых переменных 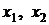. Если наступит момент, когда эти значения перестанут изменяться, то они и являются решением системы.

Переходный процесс получения установившегося решения изображен на экране виртуального осциллографа (рис. 2.3).

Рис. 2.3 Переходный процесс получения установившегося решения системы алгебраических уравнений

На рис. 2.3 видно, что после 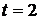на выходах виртуальных интеграторов устанавливаются сигналы, соответствующие решению системы линейных алгебраических уравнений, 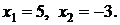Если выход на установившееся решение не происходит, то это означает, что решение системы не найдено, а саму систему следует преобразовать к виду системы с преобладающими диагональными элементами.

Пример 2. Найти решение системы алгебраических уравнений:

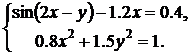
Для решения системы будем использовать блок Algebraic Constraint, который выполняет поиск корней алгебраических уравнений. Систему представим в виде

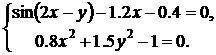
Входными сигналами схемы являются значения – 0.4 и – 1. Сгенерированные выражения для вычисления левых частей уравнений направим на входы блоков Algebraic Constraint и Algebraic Constraint1, в которых зададим начальные значения выходных сигналов Initial guess, равными, например, 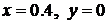соответственно.

Структурная схема модели данной системы приведена на рис. 2.4.

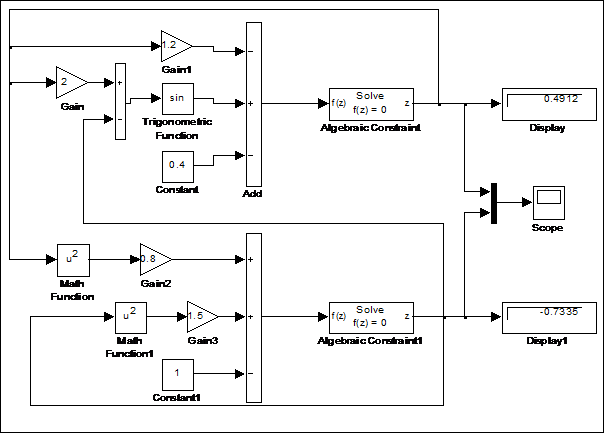
Рис. 2.4 Структурная схема модели системы алгебраических уравнений

Результатом работы модели является установившееся решение системы дифференциальных уравнений 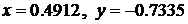, которое отображено в окнах блоков Display, Display1 (рис. 2.4), Scope (рис. 2.5), и которое является искомым решением системы алгебраических уравнений.

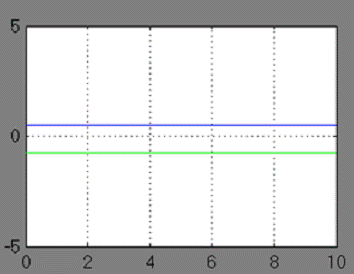
Рис. 2.5 Процесс получения решения системы алгебраических уравнений

Если изменить начальные значения выходных сигналов Initial guess блоков Algebraic Constraint и Algebraic Constraint1 на , то получим второе решение системы алгебраических уравнений .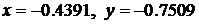

Варианты для выполнения Задания 2.1

Синтезировать структурную схему моделей статических систем и получить соответствующее решение.

При построении модели можно использовать следующие блоки: Constant, Integrator, Gain, Trigonometric Function, Math Function, Sum, Product, Mux, Display, Scope, Algebraic Constraint.

№	Система 1	Система 2

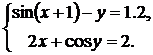
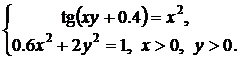
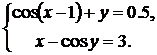
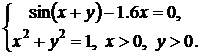
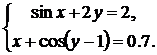
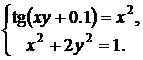
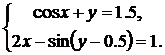
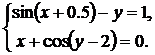
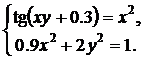
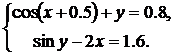
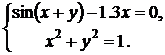
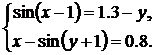
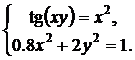
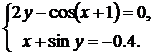
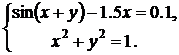
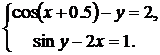
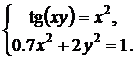
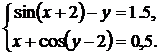
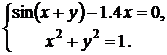
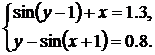
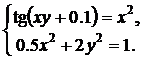
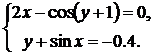
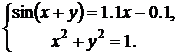
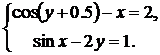
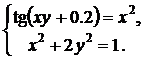
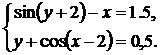
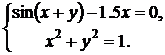
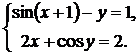
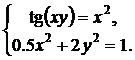
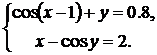
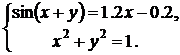
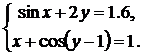
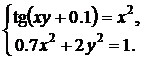
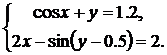
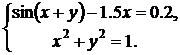
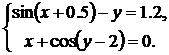
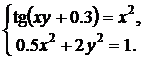
Date: 2015-07-17; view: 455; Нарушение авторских прав