Моделирование статических объектов и процессов

Исследуемые объекты и процессы называются статическими, если состояния, характеризующие эти объекты и процессы, не меняются с течением времени, то есть величины, описывающие рассматриваемые объекты и процессы, не зависят от времени, являются постоянными. Математической моделью, описывающей статические объекты и процессы, являются системы алгебраических уравнений.

Пусть статический объект описывается системой линейных алгебраических уравнений

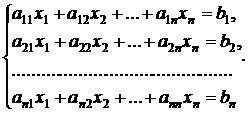
Структурную схему модели верхнего уровня (рис. 2.1) можно представить в виде блока, входными сигналами которого являются внешние воздействия, заданные величинами 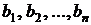, а выходными сигналами являются искомые значения переменных .

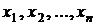Рис. 2.1 Структурная схема модели верхнего уровня

В аналоговой вычислительной технике существует несколько способов моделирования объектов, описываемых системами алгебраических уравнений. Один из них сводится к решению системы обыкновенных дифференциальных уравнений, установившееся решение которой дает решение алгебраической задачи. Еще один метод основан на применении специального блока, который выполняет поиск корней алгебраических уравнений.

Для построения модели данного объекта применим метод сведения к эквивалентной системе дифференциальных уравнений. Введем в рассмотрение следующую систему дифференциальных уравнений:

Если при решении полученной системы все производные оказываются затухающими и в итоге принимают значения, равные нулю , то на выходе получается решение системы алгебраических решений .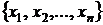

Для эквивалентности этих двух систем уравнений должно существовать установившееся решение системы дифференциальных уравнений 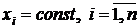. Достаточным условием, обеспечивающим существование установившегося решения, является положительная определенность матрицы коэффициентов линейной системы уравнений. Это возможно, в частности, при условии, когда матрица коэффициентов при неизвестных является матрицей с преобладающими диагональными элементами

, .

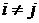Аналогичным образом можно решать систему нелинейных алгебраических уравнений вида

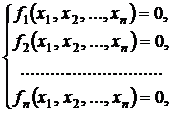
сведя ее к системе дифференциальных уравнений

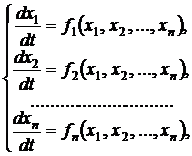
установившееся решение которой будет совпадать с решение системы алгебраических уравнений.

Выходной сигнал 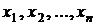получается интегрированием выражений, стоящих в правых частях дифференциальных уравнений.

Другой метод решения систем алгебраических уравнений основан на применении блока Algebraic Constraint, который выполняет поиск корней алгебраических уравнений. Блок находит такое значение выходного сигнала, при котором значение входного сигнала с течением времени становится равным нулю. При этом входной сигнал должен быть прямо или опосредованно связан с входным сигналом.

Date: 2015-07-17; view: 459; Нарушение авторских прав