Тема 4. Оптимальная политика замены производственного оборудования

(лекц. – 2 час., СРС – 20 час.)

При изучении данной темы необходимо познакомиться с общей характеристикой и отличительными особенностями задач и методов динамического программирования, с типовыми задачами перспективного планирования и стратегического управления, для которых применимы методы динамического программирования. На примере актуальной для полиграфических предприятий задачи оптимизации сроков замены оборудования следует уяснить принцип оптимальности и методику построения функциональных уравнений Р.Беллмана для выработки оптимальной политики замены машины с учетом ее физического и морального старения. Важное значение имеют вопросы подготовки исходной информации для решения задач динамического программирования и компьютерные технологии решения этих задач.

Задача оптимизации сроков замены машины рассматривается при следующих предпосылках. Анализируется плановый период продолжительностью N лет. Вследствие физического износа машины имеет место падение с течением времени ее производительности, увеличение эксплуатационных расходов и, в целом, снижение годовой прибыли от функционирования машины. Научно-технический прогресс в отрасли приводит к моральному старению эксплуатирующейся машины, которое проявляется в том, что появляются новые модели (поколения) машины с лучшими технико-экономическими показателями. Явление физического и морального старения машины учитывается в модели с помощью семейства кривых S(p,t), характеризующих зависимость годовой прибыли от возраста и поколения машины. Эта зависимость носит экспоненциальный характер и в аналитической форме может быть представлена в виде

S(p,t) =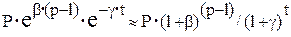

где t - возраст машин; p - индекс поколения; N – продолжительность планового периода; P - параметр, зависящий от типа машины; 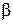- коэффициент, учитывающий моральное старение машины; - коэффициент, учитывающий физическое старение машины.

Затраты на замену машины существенно зависят от ее возраста и аналитически выражаются функцией

C(p,t) =

где R - параметр, зависящий от типа машины; 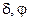- коэффициенты, учитывающие моральное и физическое старение оборудования.

Предполагается, что ежегодно появляется новая модификация (новое поколение) машины с лучшими технико-экономическими показателями по сравнению с эксплуатирующейся машиной и ранее разработанными моделями. В начале каждого года рассматриваемого планового периода принимается одно из двух альтернативных решений:

· Продолжить эксплуатацию старой машины, несмотря на то, что возраст машины увеличится еще на один год и при этом вследствие физического и морального старения произойдет дальнейшее снижение ее производительности (годовой прибыли);

· Затратив необходимую сумму средств, приобрести новую машину с тем, чтобы в текущем году и в последующие годы получать более высокую прибыль, что позволит через некоторое время компенсировать затраты на обновление машины и, возможно, накопить к концу рассматриваемого периода суммарную прибыль в большем объеме, чем при эксплуатации старой машины.

Оптимальная политика замены машины формируется из условия максимизации суммарной прибыли за весь планируемый период с учетом затрат на замену машины (инвестиций) и определяется с помощью функциональных уравнений P.Беллмана

f_n (t) = max ,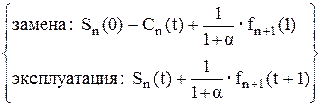

n = N-1, N-2,...,1; t = 1, 2,...,

где f_n(t) - максимальная прибыль при оптимальной политике замены за n-й и последующие годы планового периода при возрасте машины t лет к началу n-го года (следовательно, речь идет о машине (n – t)-го поколения); S_n(t) - годовая прибыль в n-м году для машины возраста t лет; C_n(t) - затраты в n-м году на замену машины возраста t лет; a - коэффициент дисконтирования, учитывающий уровень изменения цен.

Функция f полагается равной нулю для значений n 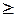N + 1. Следовательно,

f _N (t) = max ,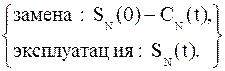

t = 1, 2,....

Вычислив значения f _N (t), t=1, 2,... и используя приведенные выше функциональные уравнения, можно найти последовательно значения f_N-1(t), f_N-2(t),..., f₁(t), t=1, 2,... при оптимальной политике замены оборудования. Значение f₁(t) соответствует суммарной прибыли от процесса эксплуатации машины, начавшегося в первый год планового периода возраста t при соблюдении в дальнейшем оптимальной стратегии замены машины. Информация, полученная в результате решения рассматриваемой задачи, позволяет разложить суммарную прибыль f₁(t) по годам планового периода и определить, сколько раз и в какие годы планового периода следует произвести замену машины, чтобы добиться наилучшего эффекта.

Отметим универсальный характер рассмотренной модели. Она может применяться для различных марок наборного, печатного и брошюровочно-переплетного оборудования полиграфических предприятий. От производственного назначения и технико-экономических характеристик машин зависят лишь значения параметров P, R и коэффициентов b, g, d, j, влияющих на интенсивность физического и морального старения оборудования.

Применение метода динамического программирования для выработки оптимальной стратегии замены оборудования связано с большим объемом вычислений. Благоприятной средой для решения рассматриваемой задачи является ЭТ Excel. При использовании ЭТ Excel обеспечивается возможность варьирования технико-экономических показателей машин в широких диапазонах с наглядным отображением исходной информации и полученных результатов в виде таблиц и графиков.

Вопросы для самопроверки

1. Охарактеризуйте особенности метода динамического программирования.

2. Для решения каких задач перспективного планирования и стратегического управления применим метод динамического программирования?

3. Опишите постановку задачи оптимизации сроков замены производственного оборудования.

4. Запишите функциональные уравнения Р.Беллмана, на основе которых формируется оптимальное решение задачи о замене оборудования.

5. Как учитывается моральный и физический износ машин при выработке оптимальной стратегии замены оборудования?

6. Какие программные средства применяются при решении задач динамического программирования?

Тема 5. Экономико-математические модели и методы
оптимального управления запасами

(лекц. – 1 час., СРС – 20 час.)

Изучение данной темы преследует цель получить общее представление о применении экономико-математических моделей и методов для оптимального управления запасами на предприятии. Необходимо рассмотреть детерминированную и стохастическую модели управления запасами, познакомиться с методами определения оптимальной периодичности поставок и объема партии в зависимости от интенсивности спроса и других производственных факторов.

В условиях производства создание запасов необходимо для обеспечения бесперебойной, ритмичной работы предприятия. Однако, необоснованное раздувание запасов ведет к ухудшению технико-экономических показателей деятельности предприятия. Математическая теория управления запасами направлена на поиск компромисса между противоречивыми требованиями надежного удовлетворения спроса и сокращения расходов на хранение потребляемой продукции.

Базовая модель задачи управления запасами в детерминированной постановке соответствует стационарному спросу на продукцию с интенсивностью m и периодическому восполнению запасов с интенсивностью l (l > m). В базовой модели допускаются отрицательные значения уровня запаса – дефицит. При положительных значениях уровня запаса предприятие несет расходы, связанные с хранением продукции. Принимается, что расходы на хранение пропорциональны уровню запаса и времени хранения. При дефиците имеют место издержки, обусловленные потерями за счет простоя оборудования, срыва поставок готовой продукции потребителям и т.д. Принимается, что штрафы за дефицит пропорциональны величине дефицита и времени его существования.

График изменения уровня запасов для базовой модели представлен на рис. 9. При построении графика рис. 9 и формировании базовой модели использованы следующие обозначения:

y(t) – текущий уровень запаса;

Y₍₊₎ – максимальный уровень запаса;

Y_(-) – максимальный уровень дефицита;

T – продолжительность цикла (периодичность возобновления поставок);

g – фиксированные расходы на возобновление поставок;

s – затраты на хранение единицы запаса в единицу времени;

r – убытки (штраф) на единицу дефицита в единицу времени.

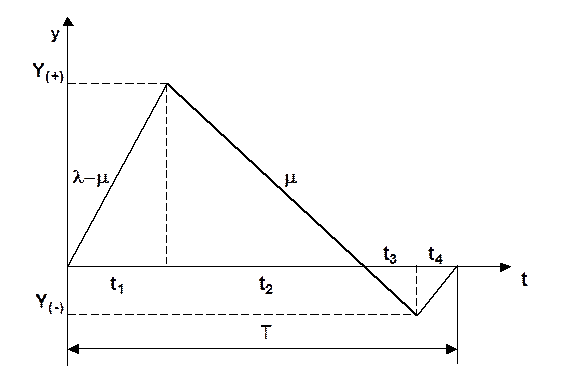
Рис. 9. Цикл изменения уровня запаса для базовой модели

Цикл изменения уровня запасов, показанный на рис. 9, включает четыре характерных отрезка времени. На первом из них, продолжительностью t₁, запасы возрастают с интенсивностью l - m от нулевого уровня до максимального Y₍₊₎. На втором отрезке, продолжительностью t₂, и на третьем отрезке, продолжительностью t₃, пополнение запасов не производится. На втором отрезке запасы снижаются с интенсивностью m от максимального до нулевого уровня. На третьем отрезке с той же интенсивностью m происходит рост дефицита от нуля до максимального уровня Y_(-). В начале четвертого отрезка, продолжительностью t₄, возобновляются поставки, дефицит уменьшается с интенсивностью l - m от максимального уровня до нуля.

В соответствии с графиком изменения уровня запаса рис. 50 общие затраты за один цикл, включающие расходы на возобновление поставок, затраты на хранение запаса и штрафы за дефицит, будут равны

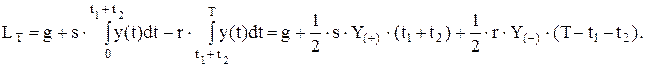
Из графика рис. 9 следует:

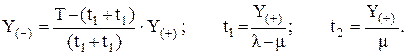
С учетом этих соотношений представим затраты, отнесенные к единице времени, как функцию максимального уровня запаса Y₍₊₎ и периодичности возобновления поставок T:

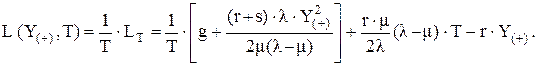
Базовая модель детерминированной задачи управления запасами соответствует поиску оптимальных значений Y₍₊₎ и T, минимизирующих затраты в единицу времени L. С позиций математики, речь идет о поиске экстремума нелинейной функции двух переменных, т.е. о задаче безусловной оптимизации, для решения которой может быть применен классический аппарат математического анализа.

Приравнивая частные производные 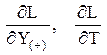к нулю, получаем систему алгебраических уравнений с двумя неизвестными:

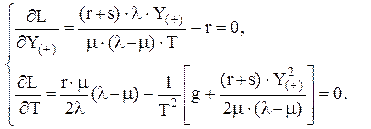
Решив данную систему, найдем оптимальные значения максимального уровня запаса и продолжительности цикла:

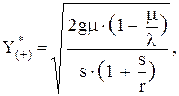
При этом достигается минимум затрат в единицу времени, равный

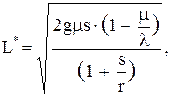
оптимальная величина дефицита равна

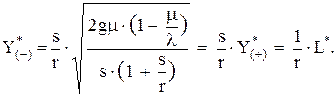
Если штраф за дефицит высок по сравнению с расходами на хранение 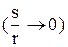и интенсивность пополнения запасов значительно превышает интенсивность спроса 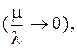то имеют место известные в теории управления запасами формулы Вильсона:

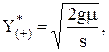
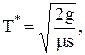
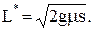
В стохастической модели управления запасами спрос рассматривается как случайная величина с известным законом распределения:

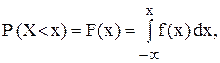
где X – случайная величина спроса в планируемом периоде T;

x – текущая величина спроса;

F(x) – интегральная функция распределения спроса;

f(x) – плотность распределения спроса.

При оптимизации системы управления запасами со случайным спросом примем в качестве целевой функции L_T – математическое ожидание расходов за период T на создание и хранение запаса с учетом штрафа за дефицит, а в качестве управляемой переменной Y – величину запаса, создаваемого на период T. Значение функции L_T вычисляется по формуле:

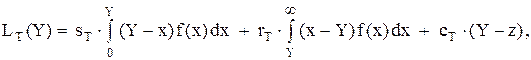
где s_T – расходы на хранение единицы запаса в период T;

r_T – штраф за каждую единицу дефицита в период T;

c_T – затраты на создание единицы запаса;

z – запас к началу планируемого периода T.

Необходимое условие минимума функции L_T(Y) записывается в виде:

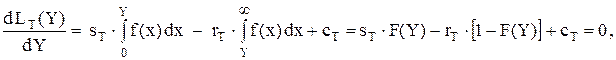
где F(Y) – интегральная функция распределения спроса при значении аргумента, равном величине создаваемого запаса на период T.

Полученное соотношение позволяет определить оптимальный уровень запаса Y*из условия

При оптимизации уровня и периодичности пополнения запасов важное значение имеет прогнозирование спроса, которое связано с анализом временных рядов. Поэтому при изучении темы необходимо рассмотреть эконометрические методы сглаживания и прогнозирования временных рядов, познакомиться с применяемыми для этой цели программными средствами.

Вопросы для самопроверки

1. В чем суть постановки классической задачи управления запасами?

2. Изобразите график изменения уровня запасов при стационарном спросе.

3. Какой математический аппарат используется для решения детерминированной задачи управления запасами при стационарном спросе?

4. Как влияют на оптимальный объем партии и периодичность поставок интенсивность спроса и затраты на хранение единицы запаса?

5. Запишите математическую модель управления запасами при случайном спросе.

6. Какие методы применяются при прогнозировании спроса?

Рекомендуемая литература

1. Просветов Г.И. Математические методы и модели в экономике: задачи и решения: учебно-практическое пособие / Г.И. Просветов. – М.: Альфа-пресс, 2008. – 344 с.

2. Исследование операций в экономике: учеб. пособие для студентов высших учеб. заведений, обучающихся по экономическим спец. и направлениям подготовки / под ред. Н.М. Кремера. – 2-е изд., перераб. и доп.; - М.: Юрайт., 2011. – 430 с.

3. Соколов А.В., Токарев В.В. Методы оптимальных решений. В 2 т. Т. 1. Общие положения. Математическое программирование., - 2-е изд., испр. – М.: ФИЗМАТЛИТ., 2011. – 564 с.

4. Голинков Ю.П. Экономико-математическое моделирование производственных систем полиграфии: Учебное пособие. – М.: МГУП, 2006.

Date: 2015-06-11; view: 1386; Нарушение авторских прав