Анализ перспектив развития производственной системы

На третьем этапе постоптимизационного анализа оцениваются перспективы развития производственной системы, вырабатываются рекомендации о радикальных путях развития производства и увеличения суммарной прибыли, которые могут быть достигнуты за счет глубоких целенаправленных изменений производственной ситуации.

Существенного эффекта в развитии производства и повышении суммарной прибыли можно добиться при комплексном наращивании производственных возможностей предприятия. Поэтому при определении перспектив развития производственной системы следует опираться на модифицированный вариант математической модели задачи планирования производства, который предполагает инвестирование денежных средств не только в приобретения дефицитных ресурсов, но и в расширение возможностей сбыта производимой продукции.

Модифицированная версия экономико-математической модели задачи планирования производства записывается в виде:

Найти мах f =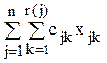

при условиях

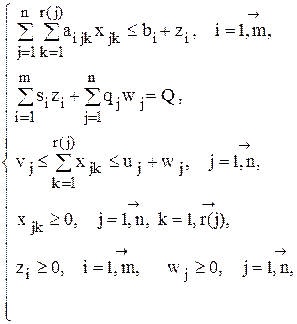
Приведем полный список обозначений для данной экономико-математической модели:

n - число видов продукции, которую может производить предприятие;

r(j), j=1,..., n - число возможных технологических вариантов изготовления продукции j-го вида;

c _jk, j=1,..., n, k=1,..., r(j) – значения удельной прибыли для продукции различного вида, изготовленной по различным технологическим вариантам;

x _jk, j=1,..., n, k=1,..., r(j) - планируемые объемы выпуска продукции различного вида с использованием различных технологических вариантов (первая группа неизвестных, оптимальные значения которых определяются при решении задачи);

m – число видов ресурсов, используемых для производства продукции;

b _i, i=1...,m – имеющиеся в наличии запасы ресурсов;

a _ijk, i=1,..., m, j=1,..., n, k=1,..., r(j) - нормы расхода ресурсов различного вида на производство продукции различного вида при применении различных технологических вариантов;

Q – сумма средств, расходуемых предприятием на приобретение дополнительных ресурсов и расширение возможностей сбыта продукции;

s _i, i=1,..., m – рыночные цены ресурсов;

z _i, i=1,..., m – дополнительно приобретаемые объемы ресурсов (вторая группа неизвестных, оптимальные значения которых определяются при решении задачи);

v _j, j=1,..., n, - обязательные объемы выпуска продукции (по госзаказу);

u _j, j=1,..., n, - объемы спроса на продукцию различного вида;

q _j, j=1,..., n – затраты денежных средств на каждую дополнительную единицу расширения спроса на продукцию различного вида;

w_j, j=1,..., n - объемы увеличения спроса на продукцию различного вида за счет денежных средств предприятия (третья группа неизвестных, оптимальные значения которых определяются при решении задачи).

На рис. 7 показана компоновка листа ЭТ Excel для проведения расчетов с использованием рассмотренной модели, предусматривающей комплексный подход к оптимальному распределению инвестиций между приобретением дополнительных ресурсов и расширением спроса на производимую продукцию.

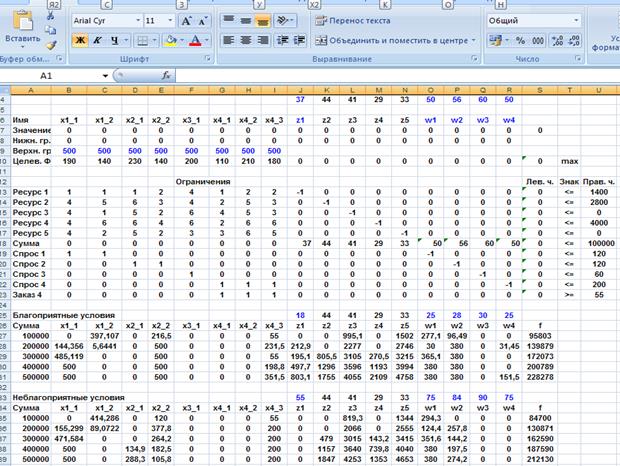
Рис. 7. Компоновка листа Excel и результаты расчетов для тестовой задачи по перспективе развития производственной системы

При оптимальном распределении инвестиций наряду с их величиной важную роль играют рыночные цены дополнительно приобретаемых ресурсов и удельные затраты на каждую дополнительную единицу расширения спроса. Их значения могут быть не известны, поэтому необходимо проводить серию расчетов, варьируя как величину инвестиций, так и рыночные цены ресурсов и удельные затраты на расширение спроса.

Рыночные цены дополнительно приобретаемых ресурсов, по которым они неизвестны (прогнозируемые цены), установить равными среднему значению от известных цен на ресурсы.

Удельные затраты на каждую дополнительную единицу расширения спроса (прогнозные уд. затраты) установить на каждый вид продукции равными 30% от среднего значения удельных прибылей по всем технологическим вариантам.

На рис. 7 представлены результаты расчетов для тестовой задачи при варьировании величины инвестиций от 100000 до 500000 д.ед. для двух вариантов удельных затрат на дополнительные ресурсы и расширение спроса – 0,5 от прогнозных значений (благоприятные условия) и 1,5 от прогнозных значений (неблагоприятные условия).

Результаты расчетов показывают, что в каждом из двух рассмотренных вариантов возможно радикальное увеличение суммарной прибыли по сравнению с той величиной (76440,6 д.ед.), которая получена ранее для номинальных условий.

График зависимости суммарной прибыли от объема инвестиций показан на рис. 8. Верхняя линия соответствует удельным затратам на дополнительные ресурсы и расширение спроса при благоприятных условиях, нижняя – при неблагоприятных условиях.

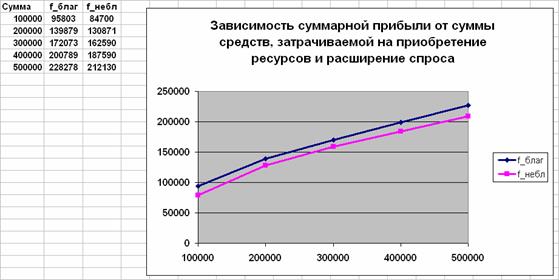
Рис. 8. Зависимость суммарной прибыли от объема инвестиций при их оптимальном распределении на приобретение ресурсов и расширение спроса

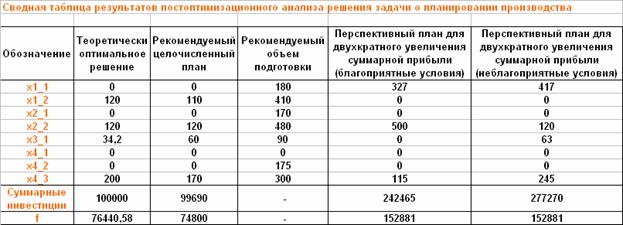
В табл. 3 подытожены результаты постоптимизационного анализа, проведенного для тестовой задачи планирования производства. Из табл. 3 следует, что рекомендуемый целочисленный план выпуска продукции совпадает по номенклатуре выпускаемой продукции с теоретически оптимальным планом, но отличается объемами выпуска трех видов продукции. Предприятию предлагается выполнить дополнительную подготовку выпуска трех видов продукции, не вошедших в теоретически оптимальное решение и рекомендуемый целочисленный план.

Перспективные планы выпуска продукции, обеспечивающие двукратное увеличение суммарной прибыли, не зависят от рассмотренных значений удельных затрат на увеличение спроса. По номенклатуре выпускаемой продукции перспективные планы существенно отличаются от исходного оптимального плана для номинальных условий, число выпускаемых видов продукции сокращается до трех. В перспективных планах предусматривается значительный объем выпуска продукции 1-го вида по 1-му технологическому варианту, который не был представлен в исходном оптимальном плане.

Таблица 3

Результаты постоптимизационного анализа для тестовой задачи
планирования производства

Вопросы для самопроверки

1. Сформулируйте постановку задачи планирования производства (оптимального распределения ресурсов), запишите экономико-математическую модель этой задачи, отражающую особенности работы предприятия в условиях рыночной экономики.

2. Какой экономический смысл имеют двойственные оценки оптимального решения задачи планирования производства.

3. Опишите технологию решения задачи планирования производства с помощью пакета “Поиск решения”.

4. Перечислите цели постоптимизационного анализа решения задачи планирования производства, опишите методику его проведения.

5. Каковы цели формирования альтернативных планов производства продукции?

6. Раскройте суть стоимостного анализа оптимального решения задачи планирования производства.

7. Изложите постановку целочисленной задачи планирования производства и методику ее решения интерактивным методом ветвей и границ.

8. В чем суть комплексного подхода к использованию инвестиций, направляемых на развитие производственной системы

9. Сформулируйте практические предложения и рекомендации, полученные Вами при решении задачи планирования производства.

Тема 2. Оптимизация загрузки производственного оборудования
(лекц. – 2 час., лаб. – 2 час., СРС – 20 час.)

Задачу оптимизации загрузки взаимозаменяемого оборудования сформулируем в следующем виде. На участке, оснащенном m разнотипными взаимозаменяемыми машинами, планируется обработка n заказов. Известны фонды машинного времени (в часах) для каждой машины a_i, i = 1, …, m; производственные задания (в учетных единицах) по каждому заказу b_j, j = 1, …, n; время, затрачиваемое на обработку одной учетной единицы каждого заказа на каждой машине t_ij, i = 1, …, m, j = 1, …, n. Кроме того, определены удельные затраты (в д.ед/уч.ед.), связанные с обработкой заказов на различных машинах c_ij, i = 1, …, m, j = 1, …, n.

Требуется так распределить заказы на машины, чтобы минимизировать суммарные затраты на выполнение производственных заданий по всем заказам, обеспечив при этом работу каждой машины в пределах располагаемого фонда машинного времени. Неизвестные в данной задаче обозначаются
x_ij, i = 1, …, m, j = 1, …, n. Первый индекс указывает тип машины, второй – вид заказа, а в целом x_ij обозначает число учетных единиц j-го заказа, обрабатываемых на i-й машине.

Базовая математическая модель задачи оптимизации загрузки взаимозаменяемого оборудования имеет вид:

Найти min f =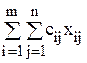

при условиях

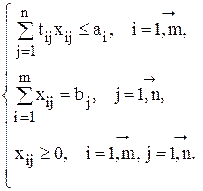
Если не допускается деление заказов на партии, обрабатываемые на разных машинах, то используется экономико-математическая модель с булевыми (двоичными) неизвестными:

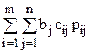Найти min f =

при условиях

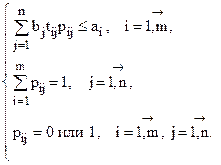p_ij равно 1, если j-й заказ распределяется на i-ю машину, и 0 в противном случае.

Возвращаясь к базовой экономико-математической модели задачи оптимизации загрузки взаимозаменяемого производственного оборудования, отметим, что в литературе по математическому программированию подобные оптимизационные задачи называются распределительными задачами. Частным случаем распределительных задач является транспортная задача.

Постановка транспортной задачи сводится к следующему. В m пунктах отправления (у поставщиков) сосредоточено a_i, i=1,...,m - единиц однородного груза, который следует доставить в n пунктов назначения (потребителям) с потребностями в грузе b_j, j=1,...,n. В базовой (закрытой) модели транспортной задачи предполагается, что суммарные запасы груза в пунктах отправления равны суммарным потребностям в грузе пунктов назначения:

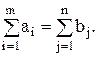
Известны затраты на перевозку единицы груза из каждого пункта отправления в каждый пункт назначения: c_ij, i=1,...,m, j=1,...,n. Необходимо найти план перевозки груза, при котором весь груз будет вывезен из пунктов отправления, в каждый пункт назначения будет доставлено требуемое число единиц груза и при этом общие затраты на перевозку груза будут минимальными.

Обозначим x_ij, i=1,...,m, j=1,...,n - число единиц груза, подлежащих перевозке из i-го пункта отправления в j-й пункт назначения, f - суммарные затраты на перевозку груза. Математическую модель закрытой транспортной задачи запишем в виде:

Найти min f =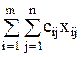

при условиях

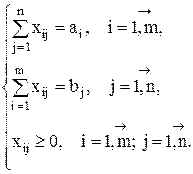
Данная модель представляет собой каноническую задачу линейного программирования с m_*n неизвестными и (m + n) ограничениями. Первая группа ограничений (первые m уравнений) соответствуют условиям вывоза груза из каждого пункта отправления во все пункты назначения в количестве, равном запасу груза в данном пункте отправления. Вторая группа ограничений (последние n уравнений) соответствуют условиям доставки груза в каждый пункт назначения из всех пунктов отправления в количестве, равном потребности в грузе данного пункта назначения.

Если суммарные запасы груза в пунктах отправления превышают суммарные потребности пунктов назначения или, наоборот, меньше суммарных потребностей, то имеет место открытая модель транспортной задачи. В первом случае ограничения первой группы, связанные с пунктами отправления, а во втором случае ограничения второй группы, связанные с пунктами назначения, записываются в виде неравенств £.

Частным случаем транспортной задачи является следующая задача о назначениях. Имеется n должностей и n претендентов на эти должности. Известна полезность каждого претендента при назначении на каждую из должностей, т.е. задана матрица c_ij, i,j=1,...,n. Требуется произвести назначение каждого претендента на одну из должностей, обеспечив при этом максимальную суммарную полезность назначений.

Обозначим через x_ij, i,j=1,...,n неизвестные, которые будут принимать значение, равное единице, если i-й претендент получает назначение на j-ю должность, и нулю - в противном случае; через f обозначим суммарную полезность назначений. Тогда математическая модель задачи о назначениях запишется в виде:

Найти max f =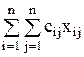

при условиях

При изучении экономико-математических моделей, представленных в данной теме необходимо внимательно разобраться с обозначениями и экономическим смыслом параметров и неизвестных в каждой из них, самостоятельно сформировать исходные данные для тестовых примеров, записать соответствующие им “числовые” модели, разработать компоновки листов Excel и настройки пакета “Поиск решения”, получить и проанализировать оптимальные решения.

Вопросы для самопроверки

1. Сформулируйте различные версии постановки задачи оптимизации загрузки взаимозаменяемого производственного оборудования, запишите соответствующие им экономико-математические модели.

2. Охарактеризуйте задачу оптимизации загрузки взаимозаменяемого производственного оборудования с позиций обобщенной модели Л.В. Канторовича.

3. К какому классу задач линейного программирования относится задача оптимизации загрузки взаимозаменяемого производственного оборудования?

4. Как соотносятся экономико-математические модели задачи оптимизации загрузки взаимозаменяемого производственного оборудования, транспортной задачи, задачи о назначениях?

5. Какие экономико-математические модели с булевыми переменными Вам известны?

6. Каким методом решаются оптимизационные задачи с булевыми неизвестными, как он реализуется в Excel?

Date: 2015-06-11; view: 641; Нарушение авторских прав